Кратко о линейном программировании
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Построение математической модели
АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Третья задача анализа на чувствительность (в каких пределах допустимо изменение коэффициентов целевой функции)
Навигация
Третья задача анализа на чувствительность (в каких пределах допустимо изменение коэффициентов целевой функции)
Решение задачи линейного программирования графическим методом
40640
знаков
2
таблицы
10
изображений
4.2.3. Третья задача анализа на чувствительность (в каких пределах допустимо изменение коэффициентов целевой функции)
Изменение цен на продукцию, т.е. изменение коэффициентов ЦФ, представляется на графике вращением целевой прямой вокруг оптимальной точки. Так, при увеличении коэффициента ЦФ 
или уменьшении 
целевая прямая вращается по часовой стрелке. При уменьшении или же увеличении целевая прямая вращается против часовой стрелки (рис.4.4).
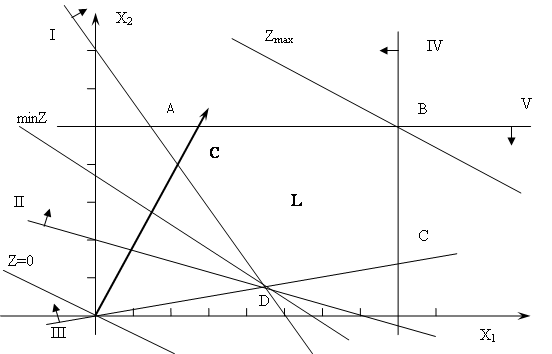
При таких поворотах точка D будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Так, например, если наклон целевой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка СD. При совпадении c прямой (2) оптимальным решением будут точки отрезка DE.
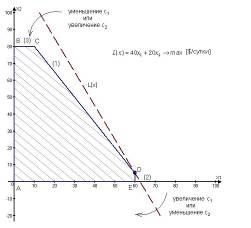
Рис.3.4. Анализ изменения цен
Наличие альтернативных оптимумов свидетельствует о том, что одно и то же оптимальное значение может достигаться при различных значениях переменных. Если целевая прямая выйдет за пределы наклона (1), то оптимальной точкой станет точка C. Допустим, что цена на радиоприемники второй модели не меняется, т.е. зафиксируем значение целевого коэффициента . Проанализируем графически результаты изменения значения целевого коэффициента , т.е. цены на радиоприемники первой модели. Оптимальное решение в точке D не будет меняться при увеличении до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оптимальное решение в точке D не будет меняться при уменьшении до тех пор, пока целевая прямая не совпадет с прямой (1).
Совпадение в процессе вращения целевой прямой с прямой ограничения означает, что углы их наклона относительно горизонтальной оси сравнялись, а значит, стали равны тангенсы углов наклона этих прямых.
Правило №5
Чтобы определить границы допустимого диапазона изменения коэффициента ЦФ, например 
и 
,
необходимо приравнять тангенс угла наклона целевой прямой 
поочередно к тангенсам углов наклона прямых связывающих ограничений, например 
и 
(рис.4.5 и 4.6).
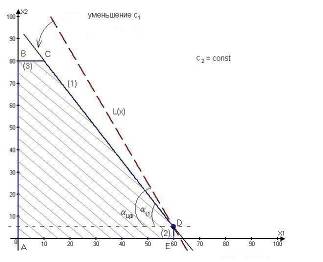
Рис.4.5. Определение
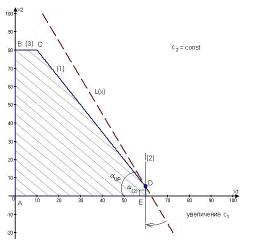
Рис.4.6. Определение
Определим, насколько максимально может снизиться цена на радиоприемники первой модели, не изменяя оптимальную точку D. Для этого применим правило №5.
Тангенсы угла наклона для прямых L(x) и (1) соответственно равны:
и 
Тогда из равенства 
находим 
[$/шт]
Теперь попробуем определить, насколько максимально может увеличиться цена на радиоприемники первой модели, чтобы не изменилась оптимальная точка D.
На рис 4.6 видно, что значение c1 можно увеличивать беспредельно, так как прямая L(x) при c2 = 20 и 
никогда не совпадает с прямой (2). Следовательно, точка D при всех значениях коэффициента 
будет единственной оптимальной.
Из приведенных выше расчетов и графической их иллюстрации следует, что если цена на радиоприемники первой модели станет меньше 30 $/шт, то наиболее выгодным будет производство радиоприемников в точке C (см. рис.4.5). При этом производительность первой технологической линии будет использоваться не в полном объеме, что приведет к недефицитности данного ресурса (2), а дефицитными будут ресурсы (1) и (3).
Проведем те же самые исследования для радиоприемников второй модели. Для этого зафиксируем значение . Ищем 
:
Тогда из равенства 
находим 
[$/шт]
На рис 4.6 видно, что значение c2 можно уменьшать до нуля, так как прямая L(x) при c1 = 40 и 
совпадает с прямой (2). Следовательно, точка D при всех значениях коэффициента 
будет оптимальной.
Аналогично делаем вывод, что если цена на радиоприемники второй модели станет выше 26,67 $/шт, то наиболее выгодным будет производство радиоприемников в точке C.
С экономической точки зрения производство радиоприемников в точке С означает, что предприятию станет выгоднее изготовлять радиоприемники второй модели, используя на полную мощность производительность второй технологической линии.
ЗАКЛЮЧЕНИЕ.
В ходе работы над курсовым проектом была рассмотрена задача линейного программирования о производстве радиоприемников. Для решения задачи использовался графический метод. Получены следующие результаты:
Оптимальная прибыль от реализации продукции достигается при следующем суточном производстве радиоприемников: 60 шт радиоприемников первой модели и 5 шт радиоприемников второй модели. При этом прибыль от реализации составит 2500$ в сутки.
Рассмотрев три задачи анализа полученного решения на чувствительность к принятой модели, мы можем ответить на следующие вопросы:
1. Определите предел увеличения производительности первой линии, превышение которого уже не будет улучшать значения целевой функции.
- предел увеличения производительности первой линии равен 63 радиоприемника в сутки. Дальнейшее увеличение производительности не имеет смысла, т.к. значение ЦФ не улучшится.
2. Определите предел уменьшения производительности второй линии, при котором полученное оптимальное решение останется неизменным.
- предельный уровень, до которого может уменьшиться производительность второй технологической линии, и при котором не изменится оптимальность полученного ранее решения, равен 5 радиоприемников в сутки.
3. Определите предел увеличения суточного запаса элементов электронных схем, при превышении которого улучшить значение целевой функции оказывается невозможным.
- предел увеличения суточного запаса элементов электронных схем равен 1700 шт в сутки. Дальнейшее увеличение нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению.
4. Определить дефицитный ресурс, который имеет наибольший приоритет при возможности увеличения запасов ресурсов.
- т.к. увеличение производительности первой технологической линии на 1 шт принесет 6,7 $/сутки (в отличии от 2$/сутки от увеличения суточного запаса элементов электронных схем), то именно данный ресурс (2) имеет приоритет.
5. Определите интервал изменения прибыли от продажи радиоприемника первой модели, в котором оптимальное решение остается неизменным.
- интервал изменения прибыли от продажи радиоприемника первой модели, в котором оптимальное решение остается неизменным, определяется неравенством 
$/шт.
6. Определите аналогичный интервал для приемника второй модели.
- интервал изменения прибыли от продажи радиоприемника второй модели, в котором оптимальное решение остается неизменным, определяется неравенством $/шт.
Решение данной задачи помогло более глубоко и основательно изучить и укрепить на практике все тонкости и моменты графического метода решения задач линейного программирования, а так же разобраться с основами анализа на чувствительность модели к полученному оптимальному решению.
Список литературы
1. АстафуровВ.Г., Колодникова Н. - Компьютерное учебное пособие, раздел “Анализ на чувствительность с помощью двойственной задачи”, Томск-2002.
2. Алесинская Т.В. - Задачи по исследованию операций с решениями.
3. Смородинский С.С., Батин Н.В. - Оптимизация решений на основе методов и моделей математического программирования: Учебное пособие.
4. Кононов В.А. - Исследование операций. Для продвинутых математиков.
Похожие работы
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... задачи f1(x)=max[g1(x)]=g1(x) – для первого предприятия; - для остальных предприятий. Решение задачи оптимального распределения средств между предприятиями методом динамического программирования Таблица 12 Средства с, тыс. гр. Предприятие 1 2 3 4 G1(x) G2(x) G3(x) G4(x) 20 11 13 12 10 40 21 20 22 27 60 40 42 34 33 80 54 45 55 57 100 62 62 ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
0 комментариев