Навигация
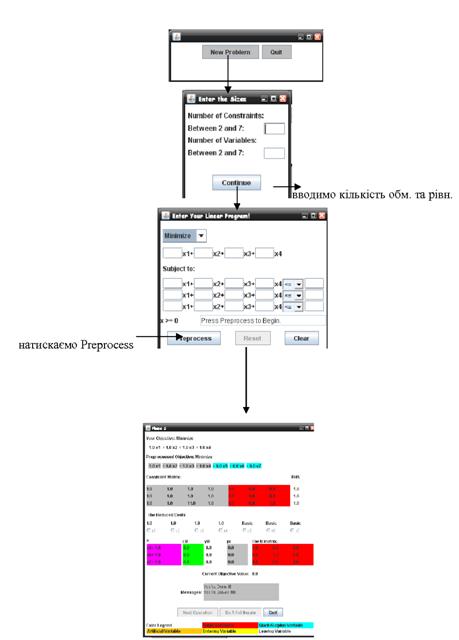
Вибір методу розв’язку задачі
1.6 Вибір методу розв’язку задачі
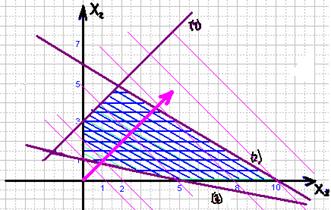
Так як симплекс-метод є універсальним, будь-яку задачу лінійного програмування можна з легкістю вирішити як за допомогою програмного забезпечення так і вручну, то для вирішення заданої задачі він підійде найкраще. За допомогою програми можна буде вирішувати велику кількість схожих задач.
2 Опис метода розв’язку задачі
Нехай у задачі представлено n видів виробничої діяльності, інтенсивності використання котрих (шукані величини) складають ![]() . Для здійснення усіх видів виробничої діяльності є в наявності видів ресурсів, можливі обсяги споживання яких обмежені значеннями
. Для здійснення усіх видів виробничої діяльності є в наявності видів ресурсів, можливі обсяги споживання яких обмежені значеннями ![]() . Витрати і-го ресурсу на одиницю продукції j-го виду виробництва дорівнюють
. Витрати і-го ресурсу на одиницю продукції j-го виду виробництва дорівнюють ![]() . Тому сума, яка являє собою загальний обсяг і-го ресурсу, що використовується n видами виробництва, не може перевищувати величини
. Тому сума, яка являє собою загальний обсяг і-го ресурсу, що використовується n видами виробництва, не може перевищувати величини ![]() .
.
Структура цільової функції ![]() відбиває внесок кожного виду виробничої діяльності в загальний результат. У випадку максимізації величина
відбиває внесок кожного виду виробничої діяльності в загальний результат. У випадку максимізації величина ![]() являє собою прибуток від j-го виду виробничої діяльності на одиницю відповідної продукції, а у випадку мінімізації
являє собою прибуток від j-го виду виробничої діяльності на одиницю відповідної продукції, а у випадку мінімізації ![]() характеризує питомі витрати. Зауважимо, що «корисність» деякого виду виробничої діяльності не можна встановити тільки за значенням відповідного коефіцієнта цільової функції, оскільки обсяг споживання обмежених ресурсів також є важливим чинником. Оскільки усі види виробничої діяльності, подані в моделі, претендують на використання обмежених ресурсів, відносна корисність деякого виду виробництва (у порівнянні з іншими видами виробничої діяльності) залежить як від величини коефіцієнта цільової функції
характеризує питомі витрати. Зауважимо, що «корисність» деякого виду виробничої діяльності не можна встановити тільки за значенням відповідного коефіцієнта цільової функції, оскільки обсяг споживання обмежених ресурсів також є важливим чинником. Оскільки усі види виробничої діяльності, подані в моделі, претендують на використання обмежених ресурсів, відносна корисність деякого виду виробництва (у порівнянні з іншими видами виробничої діяльності) залежить як від величини коефіцієнта цільової функції ![]() , так і від інтенсивності споживання ресурсів
, так і від інтенсивності споживання ресурсів ![]() . Тому можлива ситуація, коли через занадто великі витрати обмежених ресурсів деякий j-й вид виробничої діяльності, що характеризується високим прибутком, використовувати недоцільно (тобто в оптимальному розв’язку відповідна змінна виявиться небазисною).
. Тому можлива ситуація, коли через занадто великі витрати обмежених ресурсів деякий j-й вид виробничої діяльності, що характеризується високим прибутком, використовувати недоцільно (тобто в оптимальному розв’язку відповідна змінна виявиться небазисною).
В основі симплекс-методу є процес побудови початкової симплекс-таблиці, та перехід від однієї симплекс-таблиці до наступної згідно певних правил. Такі переходи виконуються доти, доки не буде виконано критерій оптимальності або не стане зрозумілим, що розв’язку не існує. Перехід від однієї симплекс-таблиці до наступної здійснюється наступним чином. Згідно певних критеріїв вибирається провідний елемент таблиці (bk,l), який стоїть на перетині рядка, який виводиться з базису, та стовпчика, який буде введено до базису. Елементи таблиці перераховуються так:
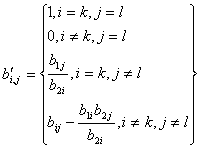 . (2.
. (2.
)
Очевидним чином дану формулу можна спростити до наступної:
![]()
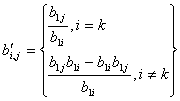 . (2.2)
. (2.2)
тобто всі елементи нової таблиці матимуть вигляд ai,j / x, де х – провідний елемент попередньої таблиці (зауваження: якщо дроби можна скоротити, то цього НЕ слід робити для правильності подальших міркувань).
Нехай тепер маємо симплекс-таблицю, що складається з цілих чисел (тобто коефіцієнти рівнянь цілі чи раціональні, що зводяться до цілих). Після першого кроку перетворень отримується така таблиця (провідний елемент дорівнює х):
Таблиця 2.1 – Симплекс-таблиця
| ¼ | ¼ | ||
| ¼ | a/x | b/x | ¼ |
| ¼ | c/x | d/x | ¼ |
| ¼ | ¼ |
Нехай на другому кроці провідним буде елемент d/x. Тоді елемент a/x перераховується за загальним правилом:
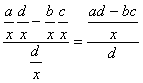 (2.3)
(2.3)
причому легко переконатися, що чисельник (ad-bc)/x буде цілим числом.
Отже, після другого кроку всі елементи знову мають загальний вигляд зі спільним знаменником, що дорівнює чисельнику провідного елемента попередньої таблиці. А в наступній таблиці чисельники будуть знову скорочуватись на цей знаменник і будуть цілими.
Якщо більш розгорнуто записати декілька переходів від однієї таблиці до іншої, то можна помітити, що числа у чисельниках та знаменниках є мінорами різних порядків, які складені з елементів початкової таблиці. Позначимо через ![]() мінор, що складений з елементів перетину рядків
мінор, що складений з елементів перетину рядків ![]() зі стовпцями
зі стовпцями ![]() початкової таблиці. Сама таблиця матиме вигляд:
початкової таблиці. Сама таблиця матиме вигляд:
Таблиця 2.2 – Симплекс-таблиця
| A11 | A21 | ... | An1 |
| A12 | A22 | ... | An2 |
| ... | ... | ... | ... |
| A1m | A2m | ... | Anm |
Процес переходу від попередньої таблиці до наступної взагалі спрощується: достатньо дописати номер рядка та стовпчика провідного елемента до всіх мінорів таблиці, що стоять у чисельниках, крім елементів того ж рядка, та до всіх мінорів знаменників (в початковій таблиці знаменник рівний одиниці).
Але слід звернути увагу на такий випадок: якщо провідний елемент опинився у тому ж рядку, що і раніше введений елемент, то “більш застарілий” слід викинути з мінору, а новий загальним чином дописати в кінець списку рядків та стовпчиків мінору відповідно. Звідси випливає, що рядки в мінорі не можуть повторюватись, тобто їх не може бути більше, ніж рівнянь обмежень, і мінори не будуть нескінченно розростатись. Але може зустрітися випадок, коли в списку стовпців, з яких складається мінор, зустрінуться однакові стовпці, тобто мінор рівний нулю. Це якраз відповідає нульовим елементам таблиці на відповідному кроці і вписується в загальне правило.
За допомогою даного методу можна набагато точніше обчислювати розв’язки задач лінійного програмування без накопичування похибки (при використанні комп’ютера), яка виникає при діленні. Цього можна досягти, якщо зберігати чисельники окремо, а знаменники взагалі завжди однакові.
Похожие работы
... зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення. Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних, Розглянемо розв' ...
... і (усі сj’ ≥0), але не задовільняє критерії допуску (не всі ві ≥0). Варіант симплекс метода, який приміняється для рішення таких задач, називається двоїстим симплекс методом. За його допомоги рішаються задачі лінійного програмування виду: (4.3.1) де система обмежень має такий вигляд і всі приведені коефіцієнти цільової функції сj’ ≥0, і=1,n. При цьому умова ві ≥0, ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
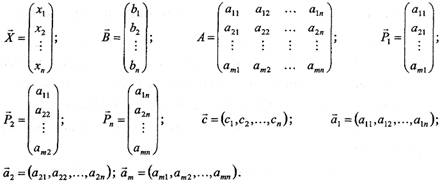
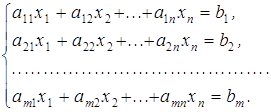
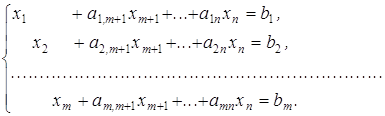
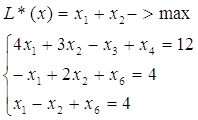
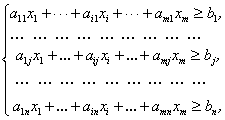
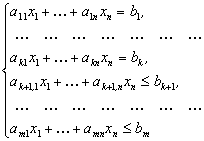
0 комментариев