Навигация
Опис вхідних та вихідних даних
35075
знаков
5
таблиц
7
изображений
4.3 Опис вхідних та вихідних даних
Дана програма написана в Excel. В ній задаються обмеження і значення цільової функції, які можна змінювати. Потім програма проводить розрахунки і в клітинках, яким попередньо були присвоєнні спеціальні імена, записує розв’язок функції мети і значення змінних, при яких цей оптимальний розв’язок був отриманий. Розглянемо всі введення даних детальніше.
Вхідними даними для даної задачі є виражені з обмежень значення кожної змінної 
та вираз для обчислення цільової функції. Значення змінних вводяться в поле «Ограничения» в меню інструменту Пошук розв'язку. Вираз значення цільової функції вводиться в комірку робочого аркуша.
Вихідними даними є значення кожної змінної та максимальне значення цільової функції, які будуть записані у визначених клітинках робочої таблиці.
4.4 Розробка структури програми
Щоб отримати розв'язок задачі лінійного програмування за допомогою Excel потрібно виконати наступні дії:
1. В заданій задачі три змінних, тому клітинкам 
потрібно присвоїти імена відповідно 
- витрати на рекламу по телебаченню; 
- витрати на радіорекламу; 
- витрати на рекламу у газетах. Для цього викликаємо команду Вставка → Имя → Присвоить. У вікні, що появилося записуємо ім’я, яке хочемо присвоїти клітинці, для першої клітинки це буде , і натиснути Enter. Для двох решти клітинок, що залишилися виконуємо аналогічні дії у присвоєнні імені. Після цього у клітинці 
аналогічно, як і для змінних, присвоюємо ім’я 
, в ній програма запише розв’язок даної задачі (рисунок 4.4.1):
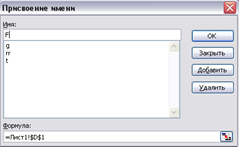
Рисунок 4.4.1 – Вікно для присвоєння імені для комірки цільової функції
2. Після цього у цій же комірці записуємо формулу для обчислення значення цільової функції у наступному вигляді: 
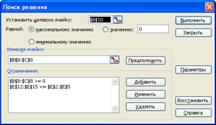
3. Запускаємо програму. Спочатку натискаємо на вкладку Сервис, що знаходиться на панелі інструментів, і в меню, що появилося, вибираємо Поиск решения (рисунок 4.4.2):
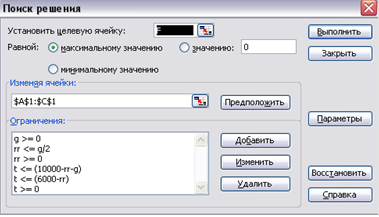
Рисунок 4.4.2 – Заповнення вікна Поиск решения
В даному діалоговому вікні встановлюємо значення цільової клітинки та зазначаємо пошук максимуму цільової функції. Задаємо клітинки, в яких буде розв'язок даної задачі — діапазон клітинок від 
до 
. За допомогою кнопки Добавить додаємо обмеження у вигляді восьми обмежень (рисунок 4.4.3):
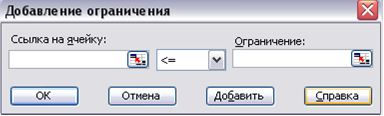
Рисунок 4.4.3 – Вікно для додавання обмежень
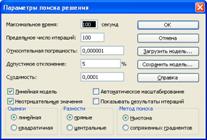
В меню Параметры відмічаємо, що модель лінійна (рисунок 4.4.4):
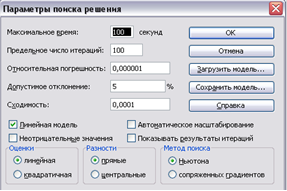
Рисунок 4.4.4 – Вікно для визначення параметрів
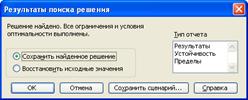
Натиснувши на кнопку Вьполнить отримуємо розв'язок задачі (рисунок 4.4.5):
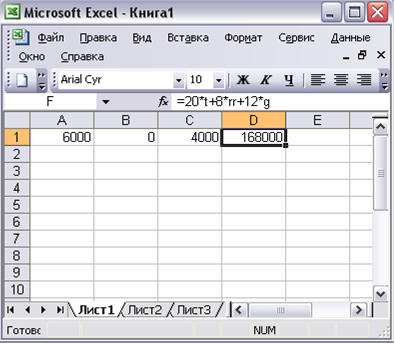
Рисунок 4.4.5 – Розв’язок даної задачі
В комірках отримали відповідні значення , а в комірці максимальне значення цільової функції.
4.5 Розробка схеми алгоритму
На рисунку 4.5.1 приведена схема алгоритму програми:
Рисунок 4.5.1 – Схема алгоритму програми
4.6 Розробка тестів
У якості тесту будемо використовувати розв'язок задачі, отриманий вручну. Для цього отриману у третьому розділі даної роботи модель заносимо до симплекс таблиці (таблиця 4.6.1):
Таблиця 4.6.1 – Ітерація 1
|
|
|
|
|
|
|
| |
|
| 1 | 1 | 1 | 1 | 0 | 0 | 10000 |
|
| 1 | 1 | 0 | 0 | 1 | 0 | 6000 |
|
| 0 | 2 | -1 | 0 | 0 | 1 | 0 |
|
| 20 | 8 | 12 | 0 | 0 | 0 | 0 |
Знаходимо базисний елемент: шукаємо стовпчик з максимальним коефіцієнтом 
і рядок з мінімальним відношенням 
/
.
Отриманий елемент є базисним елементом. Тепер змінну 
виводимо з базису, а 
вводимо в базис. Кожний елемент вибраного рядка ділимо на базисний елемент і перераховуємо таблицю за правилом прямокутника.
Елементи перераховуємо за коефіцієнтами. Отримуємо симплекс-таблицю 4.6.2.
Таблиця 4.6.2 – Ітерація 2
|
|
|
|
|
|
|
| |
|
| 0 | 0 | 1 | 1 | -1 | 0 | 4000 |
|
| 1 | 1 | 0 | 0 | 1 | 0 | 6000 |
|
| 0 | 2 | -1 | 0 | 0 | 1 | 0 |
|
| 0 | -12 | 12 | 0 | -20 | 0 | -120000 |
Перевіряємо елементи рядка . Оскільки вони всі не від’ємні і не нульові, продовжуємо розрахунок далі. Отримуємо базисний елемент. Перераховуємо таблицю, як було показано раніше. Отримуємо симплекс-таблицю 4.6.3.
Таблиця 4.6.3 – Ітерація 3
|
|
|
|
|
|
|
| |
|
| 0 | 0 | 1 | 1 | -1 | 0 | 4000 |
|
| 1 | 1 | 0 | 0 | 1 | 0 | 6000 |
|
| 0 | 2 | 0 | 1 | -1 | 1 | 4000 |
|
| 0 | -12 | 0 | -12 | -8 | 0 | -168000 |
Як бачимо, всі елементи від’ємні або дорівнюють нулю. Отже, знайдений розв’язок. Запишемо його у вигляді:
Значення змінних: 
.
Так як за умовою задачі необхідно було знайти максимум функції, але симплекс-метод дозволяє знайти лише мінімум і тому було попередньо змінено знак цільової функції, то отриманий розв’язок задачі знову потрібно помножити на -1, тому ми отримаємо наступне значення:
Цільова функція: 
.
Похожие работы
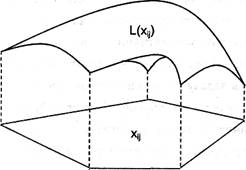
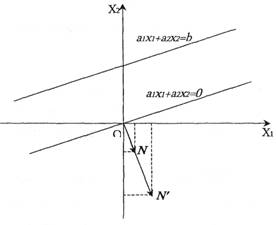
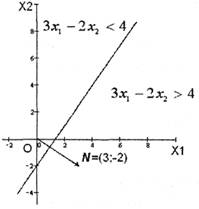
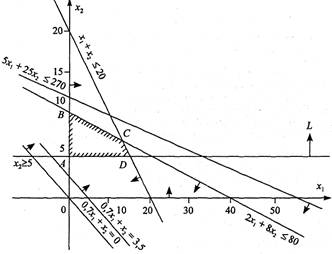
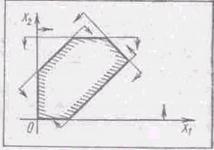
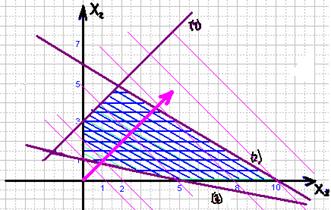
... зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення. Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних, Розглянемо розв' ...
... і (усі сj’ ≥0), але не задовільняє критерії допуску (не всі ві ≥0). Варіант симплекс метода, який приміняється для рішення таких задач, називається двоїстим симплекс методом. За його допомоги рішаються задачі лінійного програмування виду: (4.3.1) де система обмежень має такий вигляд і всі приведені коефіцієнти цільової функції сj’ ≥0, і=1,n. При цьому умова ві ≥0, ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
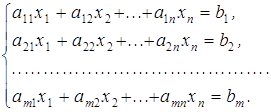
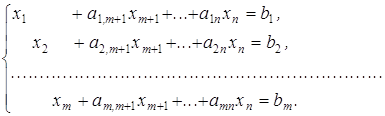
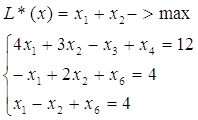
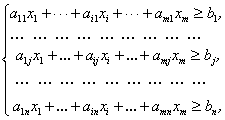
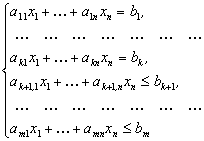
0 комментариев