Навигация
Аналіз результатів тестування
4.7 Аналіз результатів тестування
Проаналізувавши отримані результати бачимо, що значення цільової функції однакове як при вирішені задачі вручну так i при обрахунку програми.
За звичай, при обрахунку вручну появляється деяка похибка, але в даній задачі цього не відбувається, так як числа за умовою досить прості і при обрахунку ніяких заокруглень не робимо, тому отримаємо точно такі самі значення, що і при розрахунку з використання програми.
4.8 Інструкція користувачеві
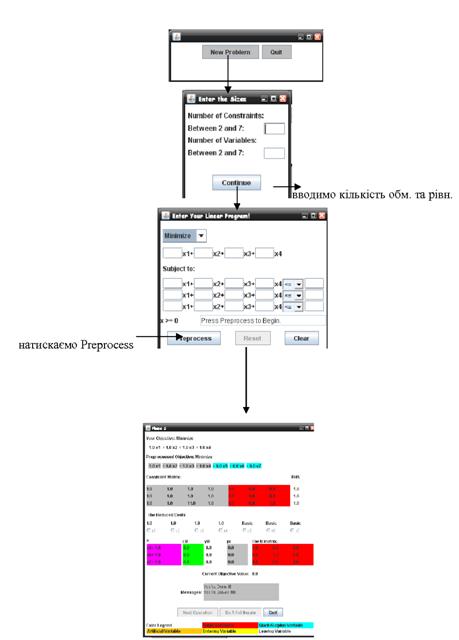
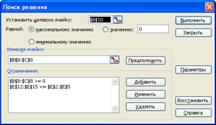
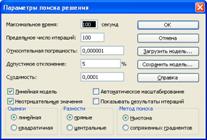
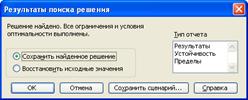
Для вирішення заданої задачі відкриваємо файл «Kursach.xls». Перед користувачем відкриється на перший погляд майже чистий лист робочої таблиці Excel, лише в комірці ![]() буде записаний нуль, але це не так. Потрібно натиснути на вкладку Сервис, що знаходиться на панелі інструментів, і в меню, що появилося, вибрати Поиск решения (див. рисунок 4.4.2). Потім у вікні, що появилося натиснути на кнопку Выполнить(див. рисунок 4.4.4) і програма все зробить сама.
буде записаний нуль, але це не так. Потрібно натиснути на вкладку Сервис, що знаходиться на панелі інструментів, і в меню, що появилося, вибрати Поиск решения (див. рисунок 4.4.2). Потім у вікні, що появилося натиснути на кнопку Выполнить(див. рисунок 4.4.4) і програма все зробить сама.
Перед користувачем з’явиться розв’язок даної задачі у вигляді як це показано на рисунку 4.4.5.
При необхідності можна змінити цільову функцію і значення параметрів. Для того, щоб змінити цільову функцію необхідно в комірці ![]() ввести ту формулу, яку необхідно. А якщо необхідно змінити обмеження, то це можна зробити у вікні Поиск решения так, як це було описано у пункті 4.4.
ввести ту формулу, яку необхідно. А якщо необхідно змінити обмеження, то це можна зробити у вікні Поиск решения так, як це було описано у пункті 4.4.
Висновки
В процесі написання даної роботи я усвідомила різницю в трактуванні понять “модель” і “метод”, необхідність поглибленого оволодіння математичними та статистичними знаннями. Приведені в роботі приклади з застосуванням математичних моделей, на мою думку, досить добре проілюстрували весь процес прийняття рішення з боку даної методології.
Незалежно від обраної професії, незалежно від життєвої ситуації людина повинна приймати раціональне рішення. Для того щоб запобігти помилок і отримати необхідну користь, потрібно розуміти весь процес прийняття рішення. Отже стає зрозуміло, що методи науки управління підвищують якість рішень, що приймаються за рахунок використання наукового підходу, системної орієнтації та моделей.
Дана курсова робота складається з багатьох розділів, що дозволяють повність зрозуміти суть проблеми, зв’язаної з оптимізацією, а також розібратися з програмним забезпеченням, що вирішує задану задачу.
Метою виконаної курсової роботи є вирішення конкретної задачі та створення програми для обчислення даних. Робота виконана з детальним описом кожного з розділів. Також приведений опис аналітичного розв'язку задачі, та порівняння результатів з розрахунком вручну.
При розв’язку задачі як в ручну так і за допомогою програми було отримано значення цільової функції та значення шуканих змінних. Тобто визначивши всі витрати на рекламу, можна отримати максимальний прибуток фірмі.
Результатом виконання даної курсової роботи є розроблена програма у найпоширенішому програмного пакеті Excel, що вирішує задачу симплекс-методом та виводить результат.
Програму можна використовувати для розрахунку різних видів оптимізації і не тільки витрат, а інших коштів, що проходять через будь-яку організацію.
Література
1. http://www.kgtu.runnet.ru/WD/TUTOR/lp/lp01.html#$lp01.1;
2. http://semenets.by.ru/public/graphic.html;
3. http://dl.sumdu.edu.ua/e-pub/mo/rus/m_simpl.html;
4. http://www.kgtu.runnet.ru/WD/TUTOR/lp/lp05.html;
5. http://dl.sumdu.edu.ua/e-pub/mo/rus/m_excel.html - Приклад розв’язку задач лінійного програмування в Excel;
6. Гавриленко В., Пархоменко Л., "Решение задач аппроксимации средствами MS EXCEL", "Компьютеры+программы", №12/2002р., с.42.http://imcs.dvgu.ru/lib/nurmi/finmath/node42.html.
Додаток А
Міністерство освіти і науки України
Вінницький національний технічний університет
Інститут автоматики, електроніки і комп’ютерних систем управління
Факультет управління та комп’ютерних систем управління
Кафедра комп’ютерних систем управління
ТЕХНІЧНЕ ЗАВДАННЯ
на виконання курсової роботи на тему:
“ Розв’язок задач лінійного програмування ”з дисципліни
“Математичне програмування та дослідження операцій”
Мета: Метою курсової роботи є розробка програмного забезпечення для розв’язку симплекс задачі
Для цього необхідно виконати наступні етапи:
1.1 Найменування та галузь застосування об’єкта розробки: Дана робота присвячена розробці програмного забезпечення для розв’язку симплекс задачі .
1.2 Підстава для проведення робіт: Підставою для розробки програмного забезпечення є навчальний план спеціальності 7.091401, робоча програма для
33
дисципліни “Математичне програмування та дослідження операцій”, індивідуальне завдання.
1.3 Дата початку роботи: “__” “______”2007р.
1.4 Дата закінчення роботи: “__” “_______”2007р.
1.5 Мета призначення розробки: Метою даної роботи є розробка програмного забезпечення для автоматизації роботи симплекс задачі.
1.6 Вимоги до надійності: Надійність даного проекту забезпечується використанням структурного програмування; а також тим, що програма працює під керівництвом єдиного меню; в ній передбачені переривання, тобто програма реагує на невірні дії користувача, вказуючи на дії, які необхідно виконати.
Все програмне забезпечення та супроводжуюча техніка документація повинні задовольняти наступним ГОСТам:
ГОСТ 19.701-90
ІСО 5807 – 85 ГОСТ на розробку програмних документів, схем, алгоритмів програм, даних та систем.
ГОСТ 19.781 – 74 – Вимоги до розробки програмного забезпечення
ГОСТ 19.101-77(СТ СЭВ 1626 - 79) – Держстандарт на розробку програмної документації, видів програм та програмних документів.
ГОСТ 29.401-78- Текст програми. Вимоги до змісту та оформлення.
ГОСТ 19.106-78- Вимоги до програмної документації.
ГОСТ 7.1- 84 та ДСТУ 3008- 95- Розробка технічної документації.
1.7 Стадії та етапи розробки:
1. Уточнення постановки задачі та розробка технічного завдання на виконання курсової роботи “Розв’язок симплекс задачі” (до 14.09.07).
2. Варіантний аналіз існуючих методів розв’язання поставленої задачі та вибір програмного середовища для вирішення задачі курсової роботи “Розв’язок симплекс задачі” (до28.09.07).
3. Розробка структури програми та наповнення файлів бази даних для розв’язку симплекс задачі (до 12.10.07).
34
4. Розробка програмного забезпечення для розв’язку симплекс задачі (до 2.11.07).
5. Розробка інтерфейсу , планування, тестування розробленої програми та створення бази даних для розв’язку симплекс задачі (до 20.11.07).
6. Демонстрація програмного забезпечення для розв’язку симплекс (до 30.11.07).
7. Розробка пояснювальної записки (до 7.12.07).
8. Захист курсової роботи (до 21.12.07).
1.8 Вимоги до безпеки: Розроблене програмне забезпечення повинно відповідати сучасним вимогам СНІП та ДЕСТів до робочого місця операторів ЕОМ.Похожие работы
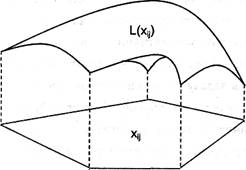
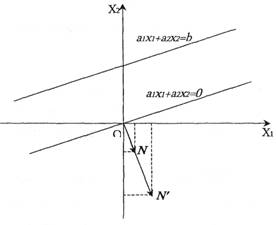
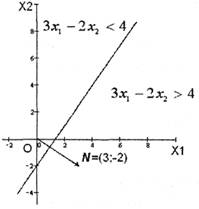
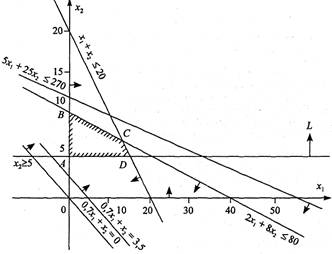
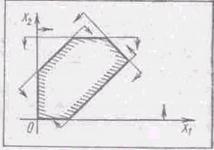
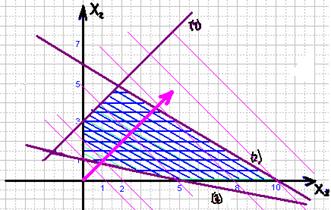
... зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення. Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних, Розглянемо розв' ...
... і (усі сj’ ≥0), але не задовільняє критерії допуску (не всі ві ≥0). Варіант симплекс метода, який приміняється для рішення таких задач, називається двоїстим симплекс методом. За його допомоги рішаються задачі лінійного програмування виду: (4.3.1) де система обмежень має такий вигляд і всі приведені коефіцієнти цільової функції сj’ ≥0, і=1,n. При цьому умова ві ≥0, ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
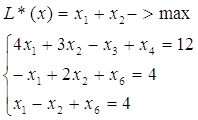
0 комментариев