Законы логики Базовые понятия

2. Законы логики Базовые понятия

Понятие, суждение, умозаключение. Истинность, ложность суждений и умозаключений. Законы логики как возведенные в принципы харак­терные черты мышления.

Обязательно изложить

Предметом логики является структура мышления, его формы и законы. Выделяются три формы мышления: понятие, суждение, умозаключение. Понятие — это форма мышления, в которой фиксируются существен­ные признаки отдельного предмета или класса однород­ных предметов. Понятия выражаются словами или груп­пами слов. Примером понятия является термин "пап­ка", обозначающий один из элементов файловой систе­мы большинства ОС. Суждение — форма мышления^ в которой что-либо утверждается или отрицается о пред­метах, их свойствах или отношениях. Суждение выра­жается в форме повествовательного предложения. Суж­дение может быть простым или сложным. Пример сужде­ния — "Папка не является файлом". Умозаключение — форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по опре­деленным правилам получается заключение.

Закон в логике понимается как требование или прин­цип, которому необходимо следовать, чтобы мышле­ние было правильным. Из многих возможных требо­ваний были выделены те, которые наиболее тесно свя­заны с такими свойствами мышления, как последова­тельность, определенность, непротиворечивость и обос­нованность: закон тождества, закон непротиворечия, закон исключенного третьего, закон достаточного ос­нования. Рассмотрим каждый из них более подробно.

Закон тождества формулируется следующим образом: "В процессе определенного рассуждения всякое поня­тие или сркдение должны быть тождественны самим себе". В мышлении этот закон выступает в качестве нор­мативного правила: в процессе рассуждения нельзя под­менять одну мысль другой, одно понятие другим. Нельзя выдавать тождественные мысли за различные, а различ­ные — за тождественные. Нарушение закона тождества приводит к двусмысленности. Например: "Откуда бе­рется хлеб? Отвечай! — Это я знаю, он печется... — Печется? О ком это он печется? — Не о ком, а из чего... Берешь зерно, мелешь его... — Не зерно ты мелешь, а чепуху!" (Л.Кэрролл. "Алиса в Зазеркалье").

Закон непротиворечия утверждает: "Два противо­положных суждения не могут быть истинными в одно и то же время и в одном и том же отношении". На­пример, суждения "Петя Иванов учится в нашем клас­се" и "Петя Иванов не учится в нашем классе" явля­ются противоречивыми, и истинным может быть лишь одно из них. Суждения "Петя Иванов учится в нашем классе" и "Петя Иванов не учился в нашем классе" могут быть непротиворечивыми, а значит, могут быть истинными или ложными одновременно.

Закон исключенного третьего формулируется следую­щим образом: "Из двух противоречащих друг другу срк-дений одно истинно, другое ложно, а третьего не дано". Действие этого закона оказывается неограниченным лишь в "жестких" предсказуемых ситуациях. Например, суж­дения "Завтра в 15 часов будет солнечное затмение" и "Завтра в 15 часов не будет солнечного затмения" под­чиняются этому закону, поскольку день и час очередного

БИЛЕТ № 10

Представление целых и вещественных чисел

I в памяти персонального компьютера.

| 2. Логическая схема триггера. Использование

I триггеров в оперативной памяти.

г 3. Задача. Разработка алгоритма (программы),

.содержащего команду (оператор) ветвления.

1. Представление целых и вещественных чисел в памяти персонального компьютера

Базовые понятия

Целые и вещественные числа.

Знаковый разряд. Дополнительный код.

Переполнение — получение результата, для сохране­ния которого в машине недостаточно двоичных разрядов.

Представление с плавающей запятой; мантисса и порядок. Нормализованные числа.

Обязательно изложить

Числовая информация была первым видом инфор­мации, который начали обрабатывать ЭВМ, и долгое время она оставалась единственным видом. Поэтому неудивительно, что в современном компьютере суще­ствует большое разнообразие типов чисел.

Целые числа. Для того чтобы различать положитель­ные и отрицательные числа, в их двоичном представле­нии выделяется знаковый разряд. По традиции исполь­зуется самый старший бит, причем нулевое значение в нем соответствует знаку плюс, а единичное — минусу.

Из сказанного следует, что положительные числа представляют собой обычное двоичное изображение числа (с нулем в знаковом бите). А вот для записи отрицательных чисел используется специальный код, называемый в, литературе дополнительным. Для прак­тического получения кода отрицательных чисел исполь­зуется Следующий алгоритм:

• модуль числа перевести в двоичную форму;

• проинвертировать каждый разряд получившегося кода, т.е. заменить единицы нулями, а нули — единицами;

• к полученному результату обычным образом при­бавит единицу.

Вещественные числа. Для хранения этого типа данных в памяти современных ЭВМ обычно использу­ется представление чисел с плавающей запятой. Оно фактически взято из математики, где любое число А в

системе счисления с основанием О предлагается запи­сывать в виде

А = (±М) • Q±f,

где М называют мантиссой, а показатель степени Р — порядком числа. Для десятичной системы это выгля­дит очень привычно, например: заряд электрона ра­вен — 1,6 • 1СГ'19 Кл, а скорость света в вакууме состав­ляет 3 • 108 м/с.

Арифметика чисел с плавающей запятой оказывается заметно сложнее, чем для целых. Тем не менее вычисли­тельные машины со всем этим великолепно умеют авто­матически справляться. Заметим, что для процессоров Intel все операции над вещественными числами вынесе­ны в отдельный функциональный узел, который принято называть математическим сопроцессором; до 486-й мо­дели он представлял собой отдельную микросхему.

Таким образом, при использовании метода представ­ления вещественных чисел с плавающей запятой в памя­ти фактически хранятся два числа: мантисса и порядок. Разрядность первой части определяет точность вычисле­ний, а второй — диапазон представления чисел.

К описанным выше общим принципам представле­ния вещественных чисел необходимо добавить прави­ла кодирования мантиссы и порядка. Эти правила могут отличаться для различных машин, и мы не будем их здесь рассматривать.

Таким образом, если сравнить между собой представ­ление целых и вещественных чисел, то станет отчетливо видно, как сильно различаются числа, скажем, 3 и 3.0.

Желательно изложить

Беззнаковые целые числа. Хотя в математиче­ских задачах не так часто встречаются величины, прин­ципиально не имеющие отрицательных значений, без­знаковые типы данных получили в ЭВМ большое рас­пространение. Причина состоит в том, что в самой машине и программах для нее имеется много такого рода объектов: прежде всего адреса ячеек, а также всевозможные счетчики (количество повторений цик­лов, число параметров в списке или символов в текс­те) . К этому списку добавим наборы чисел, обозначаю­щие дату и время, размеры графических изображений в пикселях. Все перечисленное выше принимает толь­ко целые и неотрицательные значения.

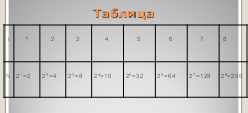
Минимальное значение для данного числового типа по определению равно 0, а максимальное состоит из единиц во всех двоичных разрядах, а потому зависит от их количества:

max- 2N- I, — где N — разрядность чисел.

Результат вычислений, например после умножения, при определенных условиях может потребовать для своего размещения большего количества разрядов, чем имеется на практике. Проблема выхода за отведен­ную разрядную сетку машины называется переполне­нием. Факт переполнения всегда фиксируется путем установки в единицу специального управляющего бита, который последующая программа имеет возможность проанализировать. Образно говоря, процессор заме­тит переполнение, но предоставляет программному обеспечению право принять решение реагировать на него или проигнорировать.

При сохранении вещественного числа некоторое неудобство вносит тот факт, что представление числа в плавающей форме не является единственным:

3 • 108= 30 • 107 = 0,3 • 109 = 0,03 • 1010 = ...

Поэтому договорились для выделения единственно­го варианта записи числа считать, что мантисса всегда меньше единицы (т.е. целая часть отсутствует), а пер­вый разряд содержит отличную от нуля цифру — в нашем примере обоим требованиям удовлетворит толь­ко число 0,3 • 109. Описанное представление чисел на­зывается нормализованным и является единственным. Любое число легко нормализуется с помощью фор­мального алгоритма.

Все сказанное о нормализации можно применять и к двоичной системе:

А = (±Л4) • 2±р, причем 1/2 < М < 1.

Существенно, что двоичная мантисса всегда начи­нается с единицы (М > 1/2). Поэтому во многих ЭВМ эта единица даже не записывается в ОЗУ, что позволяет сохранить вместо нее еще один дополни­тельный разряд мантиссы (так называемая "скрытая единица").

Примечание для учителей

Изложение, приведенное ранее в полных материа­лах билета (см. ссылку после вопроса), гораздо под­робнее, чем это необходимо для ответа на экзамене, зато представляет собой достаточно полное систе­матическое описание вопроса. Автор надеется, что знание деталей будет полезно учителю при подго­товке рассказа на уроке. В данной публикации сде­лана попытка выделить тот самый минимум, кото­рый ученику необходимо включить в свой ответ на экзамене.

Примечания для учеников

При ответе надо быть готовым к дополнительным вопросам об обосновании тех или иных утверждений. Например, каковы максимальное и минимальное зна­чения 8-битного целого числа со знаком и почему их модули не равны.

Как обычно, при подготовке вопроса необходимо продумать и подобрать примеры к своему рассказу.

Ссылка на материалы по вопросу

Полный текст материалов вопроса опубликован в "Информатике" № 11, 2003, с. 9 — 13.

Похожие работы

Различные подходы к определению количества информации. Единицы измерения количества информации

Скачать

45481

18

23

... подходе; Формы и методы: фронтальная, индивидуальная, объяснительно – иллюстративный, решение задач. Оборудование урока: демонстрационная презентация «Содержательный подход к определению количества информации. Единицы измерения количества информации» (презентация находится самом конспекте). Литература: 1.  Лапчик М.П. и др. Методика преподавания информатики: Учеб. пособие для студ. пед. вузов ...

Количество информации

Скачать

14659

4

5

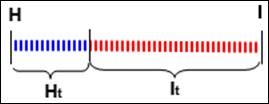
... (негэнтропия). Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H. При частичном снятии неопределенности, полученное количество информации и оставшаяся неснятой неопределенность составляют в сумме исходную неопределенность. Ht + It = H. По этой причине, формулы, которые будут представлены ниже для расчета энтропии H ...

Готовимся к экзамену по информатике

Скачать

225204

6

0

... полезно учителю при подготовке рассказа на уроке. В данной публикации сделана попытка выделить тот самый минимум, который ученику необходимо включить в свой ответ на экзамене. Примечания для учеников При ответе надо быть готовым к дополнительным вопросам об обосновании тех или иных утверждений. Например, каковы максимальное и минимальное значения 8-битного целого числа со знаком и почему их ...

Билеты и ответы по Информатике за 11-й класс

Скачать

257002

0

22

... быть выведены на печать. На экране рисунки могут быть статическими (неподвижными) или динамическими (движущимися). В последнее время машинная графика выделилась в самостоятельный раздел информатики с многочисленными приложениями. Средствами машинной графики создается не только печатная продукция, но и рекламные ролики на телевидении, мультфильмы. Объясним, как кодируется изображение в памяти ...