Математическое описание задачи перемножения сигнала и вейвлета

2.1.4.2. Математическое описание задачи перемножения сигнала и вейвлета

Анализируемый сигнал и вейвлет представляют собой массивы чисел. Размер вейвлета должен быть меньше размера сигнала, иначе результатом перемножения будет массив из нулей. Перемножение сигнала и вейвлета происходит следющим образом: вейвлет сдвигается в некоторую точку  и усредняет в данной точке значение сигнала по следующей формуле:

(2.3)

где ,  – исходный сигнал;

,  – вейвелет;

 – модуль (длина) вектора.

Полученное усреднение располагается в результате со смещением, равным половине размера вейвлета , следовательно, элементы, расположенные по краям результата на  будут равны нулю.

 

2.1.4.3. Математическое описание задачи вейвлет-анализа

Собственно сам вейвлет-анализ представляет собой процесс последовательного масштабирования исходного вейвлета и перемножения его с сигналом. В отличие от предыдущей задачи в качестве результата мы будем иметь не массив чисел, а матрицу, функция расчета точек которой уже зависит от двух параметров:

, (2.4)

где ,  – исходный сигнал;

,  – вейвлет с маштабом ;

 – модуль (длина) вектора.

Масштаб  уменьшается от  до 1.

2.2. Описание алгоритма передискретизации сигнала 2.2.1. Назначение и характеристика алгоритма передискретизации сигнала

Данный алгоритм предназначен для масштабирования дискретного сигнала (в частности вейвлета). Суть масштабирования заключается в изменении шага дискретизации с соответствующим усреднением значения сигнала.

2.2.2. Используемая информация

При реализации алгоритма используются размерные характеристики исходного и результирующего сигнала, а также собственно значения исходного сигнала.

2.2.3. Результаты решения Результатом решения является сигнал, полученный из исходного путем масштабирования. Полученный сигнал отличается от исходного тем, что его значения представлены вещественными, а не целыми числами.
2.2.4. Математическое описание алгоритма передискретизации сигнала

Математическое описание передискретизации сигнала приведено в п.

2.1.4.1. Результирующий сигнал рассчитывается по формуле (2.2).

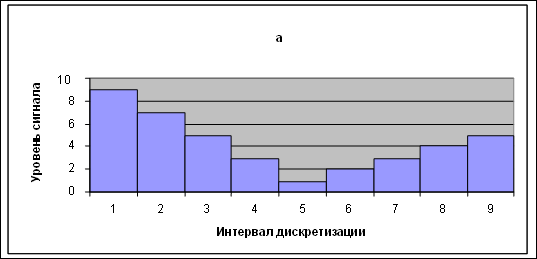
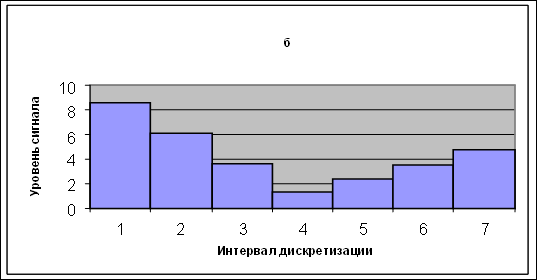
Пример передискретизации сигнала изображен на рис. 2.1.

Пример передискретизации сигнала

	а – дискретизация сигнала на 9 интервалов б – дискретизация сигнала на 7 интервалов Рис. 2.1

2.2.5. Алгоритм передискретизации сигнала

1.    i ::= 0; offs ::= 0;

2.    Если i ≥ res_size, то переход к п. 7;

3.    res_i ::= 0; j :: = 0;

4.    Если j ≥ src_size, то переход к п. 6;

5.    res_i ::= res_i + src_{](offs + j) / res_size[}; j ::= j + 1; переход к п. 4;

6.    res_i ::= res_i / src_size; i ::= i + 1; offs ::= offs + src_size; переход к п. 2;