Навигация
Вычисление статистических характеристик способом произведений
3. Вычисление статистических характеристик способом произведений.
Результаты измерений толщины кожи в мм:
| 1.23 | 1.23 | 1.28 | 1.26 |
| 1.22 | 1.25 | 1.24 | 1.24 |
| 1.26 | 1.24 | 1.21 | 1.22 |
| 1.20 | 1.25 | 1.23 | 1.25 |
| 1.21 | 1.27 | 1.25 | 1.21 |
| 1.25 | 1.24 | 1.24 | 1.27 |
| 1.28 | 1.22 | 1.20 | 1.24 |
| 1.24 | 1.23 | 1.24 | 1.26 |
| 1.26 | 1.24 | 1.27 | 1.24 |
| 1.24 | 1.26 | 1.25 | 1.24 |
При числе испытаний n=40 применяем упрощённый способ подсчёта среднего арифметического, среднего арифметического отклонения и коэффициента вариации, результаты первичных наблюдений разбиваем на разряды с определённым интервалом и определяем частоту встречаемости результатов наблюдений в каждом разделе.
По таблице 2 определяем кол-во классов, т.к. n=40, то выбираем 10 классов.
Таблица 2
| Число испытаний | 25 | 50 | 100 | 200 | 500 | более 500 |
| Количество классов | 7…11 | 8…13 | 9…14 | 10…16 | 12…18 | 14…20 |
Определяем размах результатов испытаний R. Для этого из всей совокупности результатов выбирает наибольшую Хmaxи наименьшую Хmin величины и определяем разницу между ними:
![]()
Далее определяем интервал класса (разряда):

После определения интервала класса первичные результаты группируют по разрядам и определяют частоту ni (табл.3).
Таблица 3
| Номер разрядов | Границы разрядов | Частота | Условное отклонение | Сумма S1 | Сумма S2 |
| 1 | 1.20…1.208 | 2 | -5 | -10 | 50 |
| 2 | 1.208…1.216 | 3 | -4 | -12 | 48 |
| 3 | 1.216…1.224 | 3 | -3 | -9 | 27 |
| 4 | 1.224…1.232 | 4 | -2 | -8 | 16 |
| 5 | 1.232…1.240 | 4 | -1 | -4 | 4 |
| 6 | 1.240…1.248 | 8 | 0 | 0 | 0 |
| 7 | 1.248…1.256 | 6 | +1 | 6 | 6 |
| 8 | 1.256…1.264 | 5 | +2 | 10 | 20 |
| 9 | 1.264…1.272 | 3 | +3 | 9 | 27 |
| 10 | 1.272…1.280 | 2 | +4 | 8 | 32 |
| 10 | 40 | 10 | 230 |
Определяем условное среднее значение x0 как полусумму значений нижней границы класса:
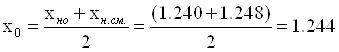
Среднее арифметическое результатов испытаний:
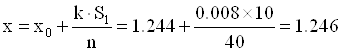
Определяем сумму квадратов отклонений![]() :
:

Вычисляем среднеквадратическое отклонение:
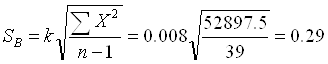
Далее определяем коэффициент вариации:
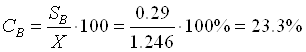
Выводы: в процессе выполнения лабораторной работы были изучены принципы и методы отбора образцов, проб и выборок при исследовании свойств текстильных материалов, способы вычисления основных статистических характеристик.
Были определены структурные характеристики, поверхностная плотность и толщина кожи классическим и упрощённым методом. При оценке толщины кожи упрощённым методом получили высокий показатель коэффициента вариации СВ. Это можно объяснить тем, что при измерении толщины был большой размах результатов испытаний R. При этом в процессе статистической обработки были удалены случайные и грубые ошибки, которые могли появиться в результате невнимательного снятия и записи показаний толщиномера, наличия погрешности в измерении прибора, неровноты толщины кожи.
Лабораторная работа №2.
Тема: Однофакторный эксперимент. Определение линейного уравнения регрессии первого порядка
Цель работы
Освоение методов математической обработки результатов исследования свойств текстильных материалов; определение уравнения регрессии по данным однофакторного эксперимента.
Пособия и инструменты: таблицы значений критериев Кочрена, Стьюдента, Фишера; микрокалькулятор.
Содержание работы
1. Статистическая обработка первичных результатов эксперимента.
2. Расчет критерия Кочрена и проверка однородности дисперсии в опытах матрицы.
3. Определение средней дисперсии выходного параметра в опытах матрицы.
4. Определение коэффициентов регрессии и составление уравнения регрессии.
5. Определение адекватности уравнения регрессии. Расчет критерия Фишера.
6. Оценка значимости коэффициентов регрессии.
7. Определение доверительных интервалов средних и индивидуальных значений выходного параметра.
8. Построение графика полученного уравнения регрессии.
9. Анализ результатов работы. Формулировка выводов.
Общие сведения
В настоящее время при исследовании свойств текстильных материалов и других видов продукции широкое применение получили математико-статистические методы планирования экспериментов.
В задачу планирования эксперимента входят: выбор необходимых для эксперимента опытов, т.е. построение матрицы планирования, выбор методов математической обработки результатов эксперимента.
Существует два вида планирования активного эксперимента: традиционное (классическое) однофакторное и многофакторное (факторное).
В традиционном однофакторном планировании изучается влияние на выходной параметр одного входного параметра (фактора).
В результате обработки экспериментальных данных определяют взаимосвязь между выходным параметром (Y) и варьируемым на нескольких уровнях фактором (X). Математическая модель в общем виде описывается функцией отклика:
y = f(x) (1)
При существовании линейной связи между входными и выходными параметрами уравнение регрессии имеет следующий вид:
y = do+d1(x-x̃), (2)
где d0,d1 – коэффициенты уравнения регрессии.
Адекватность уравнения регрессии проверяется по критерию Фишера [1,4]. Если расчетное значение критерия Фишера (Fp) меньше табличного (Fm), то гипотеза об адекватности линейной модели не отвергается.
Выполнение работы
Похожие работы
... Но, дешевые товары не всегда имеют пониженное качество. Ряд товаров повседневного спроса устанавливаются определенное ограничение цен или торговых надбавок. Б (4/1) Классификация как метод товароведения: иерархический, фасетный методы классификации, правила классификации. Классификация - разделения множества объектов на подмножества по сходству или различию в соответствии с принятыми методами. ...
0 комментариев