Навигация
Оценка значимости коэффициентов регрессии
6. Оценка значимости коэффициентов регрессии
Для определения значимости полученных коэффициентов d0 и d1 уравнения (8) используется критерий Стьюдента [1], расчетное значение которого определяем по формуле
tp=|di|/S{di}=3,114 (12)
где S {di} - оценка среднеквадратического отклонения коэффициента регрессии di.
Дисперсию коэффициентов регрессии S2{do} и S2{d1} рассчитываем по формулам:
![]() (13)
(13)
 (14)
(14)
В формулы (13) и (14) входит дисперсия S2{y}, которая является сводной оценкой дисперсии случайной величины Yu выходного параметра при условии линейной связи. Эту дисперсию определяем по формуле
![]() (15)
(15)
далее определяют число степеней свободы этой дисперсии:
f{S2}=mN-2=58(16)
Сравниваем табличное и расчётное значения критерия Стьюдента. Если tp>tт, то коэффициенты уравнения регрессии значимы и, следовательно, связь между Y и Х значима.
В нашем случае tр=3,114, а tt=2,0. Следовательно, связь между Y и Х значима.
После этого определяем абсолютные ошибки коэффициентов регрессии ε{di}:
ε {di}=S{di}·tT[α,f{S2}]. (17)
ε {d0}=2,314
ε {d1}=0,035
Тогда для истинных значений коэффициентов регрессии δ0 и δ1 в линейном уравнении (8) доверительные интервалы определяются неравенством
di-ε{di}≤ δi≤ds+ ε{di}. (18)
6,961≤ δ0≤5,289
-0,036967≤ δ1≤-0,033
7. Определение доверительных интервалов средних и индивидуальных значений выходного параметра
Чтобы определить степень отклонения расчетных значений выходного параметра YRu от истинного его значения при каждом уровне фактора Xu, определяем доверительные ошибки ε{YRu} расчетного значения выходного параметра и доверительные интервалы средних и индивидуальных значений выходного параметра.
Доверительные ошибки расчетных значений выходного параметра для каждого уровня фактора рассчитывают по формуле
εm{YRu}=Sm{yRu}·tT[α,f{S2}] (19)
где Sm{yRu} – оценка среднеквадратического отклонения расчетного значения выходного параметраYRu для каждого значения xu.
Оценку среднеквадратического отклонения рассчитывают по формуле
![]() (20)
(20)
Расчеты εm{YRu} и Sm{YRu} заносим в табл.4.
Далее в таблицу заносят расчетные значения yRu, полученные по уравнению регрессии (8).
Зная ошибки расчетной величины, определяем доверительные интервалы для испытанных средних значений выходного параметра.
Нижний доверительный интервал определяют:
Ym(н)=yRu- εm,(21)
верхний доверительный интервал :
Ym(в)=yRu+ εm, (22)
Значения верхних и нижних значений доверительных интервалов для каждого опыта заносим в табл. 4.
Таблица 4
Доверительные интервалы средних значений
| u | xu | (xu- x̃)2 | Sm2 | Sm | εm | YRu | Ym(н) | Ym(в) |
| 1. | 4 | 12225.06 | 4.871e | 0.070 | 8.096 | 9.492 | 1.397 | 17.588 |
| 2. | 12 | 10519.99 | 4.192e | 0.065 | 7.510 | 9.477 | 1.967 | 16.987 |
| 3. | 20 | 8942.91 | 3.563e | 0.060 | 6.924 | 9.461 | 2.537 | 16.385 |
| 4. | 27 | 7667.98 | 3.055e | 0.055 | 6.412 | 9.447 | 3.035 | 15.859 |
| 5. | 35 | 6331.38 | 2.523e | 0.050 | 5.826 | 9.431 | 3.605 | 15.258 |
| 6. | 43 | 5121.84 | 2.041e | 0.045 | 5.241 | 9.416 | 4.175 | 14.656 |
| 7. | 50 | 4168.89 | 1.661e | 0.041 | 4.728 | 9.402 | 4.674 | 14.130 |
| 8. | 58 | 3199.83 | 1.275e | 0.036 | 4.142 | 9.386 | 5.244 | 13.529 |
| 9. | 66 | 2358.75 | 9.401e | 0.031 | 3.557 | 9.370 | 5.814 | 12.927 |
| 10. | 73 | 1727.82 | 6.888e | 0.026 | 3.044 | 9.357 | 6.312 | 12.401 |
| 11. | 81 | 1126.74 | 4.493e | 0.021 | 2.459 | 9.341 | 6.882 | 11.800 |
| 12. | 88 | 705.81 | 2.816e | 0.017 | 1.947 | 9.327 | 7.381 | 11.274 |
| 13. | 96 | 344.73 | 1.377e | 0.012 | 1.361 | 9.312 | 7.950 | 10.673 |
| 14. | 104 | 111.66 | 4.488e | 0.0067 | 0.777 | 9.296 | 8.519 | 10.073 |
| 15. | 111 | 12.72 | 5.467e | 0.002338 | 0.271 | 9.282 | 9.011 | 9.553 |
| 16. | 119 | 19.65 | 8.228e | 0.002868 | 0.333 | 9.266 | 8.934 | 9.599 |
| 17. | 126 | 130.71 | 5.247e | 0.007244 | 0.840 | 9.253 | 8.412 | 10.093 |
| 18. | 134 | 377.64 | 1.509e | 0.012 | 1.425 | 9.237 | 7.812 | 10.662 |
| 19. | 141 | 698.70 | 2.788e | 0.017 | 1.937 | 9.223 | 7.286 | 11.160 |
| 20. | 149 | 1185.63 | 4.728e | 0.022 | 2.522 | 9.207 | 6.685 | 11.729 |
| 21. | 156 | 1716.69 | 6.843e | 0.026 | 3.035 | 9.194 | 6.159 | 12.228 |
| 22. | 164 | 2443.62 | 9.739e | 0.031 | 3.620 | 9.178 | 5.558 | 12.798 |
| 23. | 171 | 3184.68 | 1.269e | 0.036 | 4.133 | 9.164 | 5.031 | 13.297 |
| 24. | 179 | 4151.61 | 1.654e | 0.041 | 4.718 | 9.148 | 4.430 | 13.867 |
| 25. | 186 | 5102.67 | 2.033e | 0.045 | 5.231 | 9.135 | 3.904 | 14.365 |
| 26. | 194 | 6309.60 | 2.514e | 0.050 | 5.816 | 9.119 | 3.302 | 14.935 |
| 27. | 201 | 7470.66 | 2.977e | 0.055 | 6.329 | 9.105 | 2.776 | 15.434 |
| 28. | 209 | 8917.59 | 3.553e | 0.060 | 6.915 | 9.089 | 2.175 | 16.004 |
| 29. | 216 | 10288.65 | 4.099e | 0.064 | 7.427 | 9.076 | 1.648 | 16.503 |
| 30. | 224 | 11975.58 | 4.771e | 0.069 | 8.013 | 9.060 | 1.047 | 17.073 |
Далее определяем границы доверительного интервала для индивидуальных значений выходного параметра Y при каждом уровне фактора.
Верхняя граница интервала:
yl(в)=yRu+Sl·tт[α,f{S2}]. (23)
Нижняя граница интервала:
yl(в)=yRu-Sl·tт[α,f{S2}]. (23)
Предварительно определяем ошибку:
![]() (25)
(25)
Используя значения Sm из табл. 4 и ранее определенные по уравнению (15) значения S2{у} и критерий Стьюдента, определяем верхние и нижние границы искомой зоны по формулам (23) и (24), сводя все расчеты в табл. 5,
Таблица 5
| u | xu | Sm2 | Sl2 | Sl | YRu | tт· Sl | Yl(н) | Yl(в) |
| 1. | 4 | 4.871e | 0.107 | 0.328 | 9.492 | 0.656 | 8.837 | 10.148 |
| 2. | 12 | 4.192e | 0.107 | 0.327 | 9.477 | 0.653 | 8.823 | 10.130 |
| 3. | 20 | 3.563e | 0.106 | 0.326 | 9.461 | 0.652 | 8.809 | 10.112 |
| 4. | 27 | 3.055e | 0.106 | 0.325 | 9.447 | 0.650 | 8.797 | 10.097 |
| 5. | 35 | 2.523e | 0.105 | 0.324 | 9.431 | 0.648 | 8.783 | 10.080 |
| 6. | 43 | 2.041e | 0.105 | 0.323 | 9.416 | 0.647 | 8.769 | 10.063 |
| 7. | 50 | 1.661e | 0.104 | 0.323 | 9.402 | 0.646 | 8.756 | 10.048 |
| 8. | 58 | 1.275e | 0.104 | 0.322 | 9.386 | 0.644 | 8.742 | 10.031 |
| 9. | 66 | 9.401e | 0.103 | 0.322 | 9.370 | 0.643 | 8.727 | 10.014 |
| 10. | 73 | 6.888e | 0.103 | 0.321 | 9.357 | 0.643 | 8.714 | 9.999 |
| 11. | 81 | 4.493e | 0.103 | 0.321 | 9.341 | 0.642 | 8.699 | 9.983 |
| 12. | 88 | 2.816e | 0.103 | 0.321 | 9.327 | 0.641 | 8.686 | 9.969 |
| 13. | 96 | 1.377e | 0.103 | 0.320 | 9.312 | 0.641 | 8.671 | 9.952 |
| 14. | 104 | 4.488e | 0.103 | 0.320 | 9.296 | 0.641 | 8.655 | 9.936 |
| 15. | 111 | 5.467e | 0.103 | 0.320 | 9.282 | 0.640 | 8.642 | 9.923 |
| 16. | 119 | 8.228e | 0.103 | 0.320 | 9.266 | 0.640 | 8.626 | 9.907 |
| 17. | 126 | 5.247e | 0.103 | 0.320 | 9.253 | 0.641 | 8.612 | 9.893 |
| 18. | 134 | 1.509e | 0.103 | 0.320 | 9.237 | 0.641 | 8.596 | 9.878 |
| 19. | 141 | 2.788e | 0.103 | 0.321 | 9.223 | 0.641 | 8.582 | 9.864 |
| 20. | 149 | 4.728e | 0.103 | 0.321 | 9.207 | 0.642 | 8.565 | 9.849 |
| 21. | 156 | 6.843e | 0.103 | 0.321 | 9.194 | 0.643 | 8.551 | 9.836 |
| 22. | 164 | 9.739e | 0.104 | 0.322 | 9.178 | 0.644 | 8.534 | 9.821 |
| 23. | 171 | 1.269e | 0.104 | 0.322 | 9.164 | 0.644 | 8.520 | 9.808 |
| 24. | 179 | 1.654e | 0.104 | 0.323 | 9.148 | 0.646 | 8.503 | 9.794 |
| 25. | 186 | 2.033e | 0.105 | 0.323 | 9.135 | 0.647 | 8.488 | 9.781 |
| 26. | 194 | 2.514e | 0.105 | 0.324 | 9.119 | 0.648 | 8.471 | 9.767 |
| 27. | 201 | 2.977e | 0.106 | 0.325 | 9.105 | 0.650 | 8.455 | 9.755 |
| 28. | 209 | 3.553e | 0.106 | 0.326 | 9.089 | 0.651 | 8.438 | 9.741 |
| 29. | 216 | 4.099e | 0.107 | 0.327 | 9.076 | 0.653 | 8.422 | 9.729 |
| 30. | 224 | 4.771e | 0.107 | 0.328 | 9.060 | 0.655 | 8.405 | 9.715 |
Выводы: в процессе выполнения лабораторной работы были изучены методы математической обработки результатов исследования свойств текстильных материалов, приведён расчёт критерия Кочрена и проверка однородности дисперсии в опытах матрицы, определена средняя дисперсия выходного параметра в опытах матрицы, коэффициенты регрессии, адекватность уравнения регрессии, расчёт критерия Фишера, определены уравнения регрессии по данным однофакторного эксперимента, доверительные интервалы средних и индивидуальных значений выходного параметра, построен график полученного уравнения регрессии.
Лабораторная работа №3 часть 1
Постановка полного факторного эксперимента при исследовании качества швейных изделий. Определение многофакторных регрессионных моделей I и II порядков при исследовании качества швейных изделий
Цель работы:
Освоить математические методы планирования полного факторного эксперимента (ПФЭ); научиться определять математические модели I и II порядков при исследовании качества швейных изделий
Содержание работы
1 .Планирование полного факторного эксперимента и обработка результатов.
2. Определение линейной модели ПФЭ.
3. Проверка адекватности уравнения I порядка.
4. Планирование многофакторного эксперимента II порядка.
5. Определение уравнения регрессии II порядка.
6. Проверка адекватности уравнения II порядка.
7. Анализ результатов работы. Формулировка выводов.
Пособия и инструменты: таблицы значений критериев Стьюдента, Фишера; микрокалькулятор.
Вариант №4
Определяли воздухопроницаемость тканей с различными значениями плотности нитей по основе (Х1)(П0=180), и коэффициентом уплотненности (Х2)(С0=0,7) с интервалами изменения соответственно 50 и 0,2. Определить уровни варьирования факторов, построить рабочую матрицу планирования. Провести обработку ПФЭ, найти уравнение регрессии, проверить его адекватность, результаты расчёта представить графически.
Матрица эксперимента
| № опыта | Х0 | Х1 | Х2 | Х1Х2 | Y дм/м ·с |
| 1 2 3 4 | + + + + | + - + - | - - + + | - + + - | 200 380 150 300 |
Общие сведения
Качество швейных изделий зависит от целого ряда факторов (свойства используемых материалов, швейных ниток, качество соединений и др.). Поэтому при исследовании качества швейных изделий решают многофакторную задачу, в которой изучаемое свойство объекта (Y) зависит от нескольких факторов (Х1 , Х2, Х3, Х4 и т.д.).
С той целью проводится полный факторный эксперимент (ПФЭ), в котором реализуются все возможные комбинации рассматриваемых уравнений факторов, а результаты оцениваются с помощью статистического анализа.
Планирование ПФЭ связано с построением линейных моделей вида
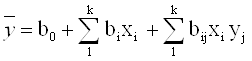
где ![]() - значение критерия;
- значение критерия;
bi - линейные коэффициенты;
bij— коэффициенты двойного взаимодействия факторов.
Многофакторный эксперимент представляет собой сложную задачу, поэтому очень часто линейная математическая модель является неадекватной реальному процессу.
В данном случае переходят к планированию второго и более высоких порядков. Уравнение регрессии при этом представляет полином второй или более высокой степени. Так, при планировании второго порядка изучаемый процесс описывается уравнением второго порядка, общий вид которого представлен ниже
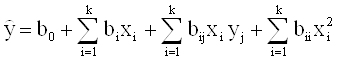
Порядок статистической обработки результатов эксперимента при многофакторном планировании соответствует последовательности обработки при однофакторном планировании.
Выполнение работы
1.1. Определение коэффициентов уравнения регрессии.
1.1.1. Свободный член уравнения регрессии определяем по формуле:
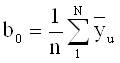
![]()
где n - число опытов;
![]() - средний результат в каждом опыте.
- средний результат в каждом опыте.
1.1.2. Линейные коэффициенты определяют по формуле:
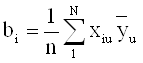
![]()
![]()
где хiu - кодированное значение i-го фактора в каждом отдельном опыте.
1.1.3. Коэффициенты парного взаимодействия.
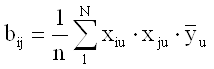
![]()
1.2. Оценка значимости коэффициентов уравнения регрессии.
1.2.1 Определение дисперсии результатов эксперимента:

где  – сумма среднеквадратических отклонений результатов эксперимента от среднего значения в каждом определенном опыте;
– сумма среднеквадратических отклонений результатов эксперимента от среднего значения в каждом определенном опыте;
N - повторность опытов.
![]()
1.2.2 Определение дисперсии (ошибки) коэффициентов уравнения регрессии по формуле
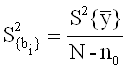
1.2.3. Определение доверительного интервала для коэффициентов уравнения.
![]()
где tT= 3,18-табличное значение критерия Стьюдента для n=4.
![]()
![]()
После определения доверительного интервала сравниваем его величину с коэффициентами регрессии. Величина доверительного интервала меньше (по модулю) величины коэффициента, следовательно, данный коэффициент уравнения значим и не исключается из уравнения регрессии.
Похожие работы
... Но, дешевые товары не всегда имеют пониженное качество. Ряд товаров повседневного спроса устанавливаются определенное ограничение цен или торговых надбавок. Б (4/1) Классификация как метод товароведения: иерархический, фасетный методы классификации, правила классификации. Классификация - разделения множества объектов на подмножества по сходству или различию в соответствии с принятыми методами. ...
0 комментариев