Навигация
Расчёт критерия Кочрена и проверка однородности дисперсии в опытах матрицы
2. Расчёт критерия Кочрена и проверка однородности дисперсии в опытах матрицы
Для проверки однородности дисперсии и воспроизводимости эксперимента при одинаковой повторности (m) всех опытов рассчитываем значение критерия Кочрена Gp по формуле
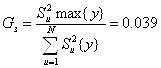 (3)
(3)
где ![]() - максимальная дисперсия из всех опытов;
- максимальная дисперсия из всех опытов;
![]() - сумма всех дисперсий эксперимента.
- сумма всех дисперсий эксперимента.
Далее расчётное значение Gp сравниваем с табличным значением GT. Дисперсии однородны и число повторных опытов одинаково, т.к. Gp< GT(0.039<0.3632).
3. Определение средней дисперсии выходного параметра в опытах матрицы
Т.к. в опытах матрицы дисперсии однородны и число повторных опытов одинаково, то среднюю дисперсию определяют по формуле
 (4)
(4)
После этого определяем число степеней свободы средней дисперсии;
F(S2(1){y})=N(m-1)=30 (5)
Средняя дисперсия характеризует средний разброс значений выходного параметра относительно его средних значений, т.е. ошибку опытов в эксперименте.
4. Определение коэффициентов регрессии и составление уравнения регрессии
Дисперсии выходного параметра для каждого уровня фактора однородны, следлвательно, применяем метод наименьших квадратов.
Коэффициенты уравнения регрессии определяем по формулам:
 (6)
(6)
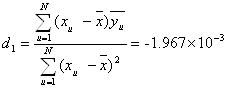 (7)
(7)
где ![]() - среднее значение результата эксперимента;
- среднее значение результата эксперимента;
xu - значение фактора на определенном u-уровне;
![]() - среднее значение фактора.
- среднее значение фактора.
Для удобства все промежуточные расчеты сводят в табл. 2.
Таблица 2
Расчет коэффициентов уравнения регрессии
| № опыта u | Фактор xu | xu- x̃ | (xu- x̃)2 | Ỹu | (xu- x̃) Ỹu |
| 1. | 4 | -110.567 | 12225.06 | 9.70 | -1072.49 |
| 2. | 12 | -102.567 | 10519.99 | 9.56 | -980.54 |
| 3. | 20 | -94.567 | 8942.91 | 9.48 | -896.49 |
| 4. | 27 | -87.567 | 7667.98 | 9.45 | -827.51 |
| 5. | 35 | -79.567 | 6331.38 | 9.42 | -749.52 |
| 6. | 43 | -71.567 | 5121.84 | 9.39 | -672.01 |
| 7. | 50 | -64.567 | 4168.89 | 9.37 | -604.99 |
| 8. | 58 | -56.567 | 3199.83 | 9.34 | -528.34 |
| 9. | 66 | -48.567 | 2358.75 | 9.32 | -452.64 |
| 10. | 73 | -41.567 | 1727.82 | 9.32 | -387.40 |
| 11. | 81 | -33.567 | 1126.74 | 9.30 | -312.17 |
| 12. | 88 | -26.567 | 705.81 | 9.29 | -246.81 |
| 13. | 96 | -18.567 | 344.73 | 9.27 | -172.12 |
| 14. | 104 | -10.567 | 111.66 | 9.26 | -97.85 |
| 15. | 111 | -3.567 | 12.72 | 9.24 | -32.96 |
| 16. | 119 | 4.433 | 19.65 | 9.23 | 40.92 |
| 17. | 126 | 11.433 | 130.71 | 9.22 | 105.41 |
| 18. | 134 | 19.433 | 377.64 | 9.21 | 178.98 |
| 19. | 141 | 26.433 | 698.70 | 9.21 | 243.45 |
| 20. | 149 | 34.433 | 1185.63 | 9.20 | 316.78 |
| 21. | 156 | 41.433 | 1716.69 | 9.18 | 380.35 |
| 22. | 164 | 49.433 | 2443.62 | 9.18 | 453.79 |
| 23. | 171 | 56.433 | 3184.68 | 9.17 | 517.49 |
| 24. | 179 | 64.433 | 4151.61 | 9.15 | 589.56 |
| 25. | 186 | 71.433 | 5102.67 | 9.14 | 652.89 |
| 26. | 194 | 79.433 | 6309.60 | 9.14 | 726.60 |
| 27. | 201 | 86.433 | 7470.66 | 9.13 | 489.13 |
| 28. | 209 | 94.433 | 8917.59 | 9.13 | 862.17 |
| 29. | 216 | 101.433 | 10288.65 | 9.13 | 926.08 |
| 30. | 224 | 109.433 | 11975.58 | 9.12 | 998.02 |
После определения коэффициентов составляют искомое уравнение регрессии:
yR = do+d1(x-x̃). (8)
5. Определение адекватности уравнения регрессии. Расчеты критерия Фишера. Для определения адекватности полученного уравнения (8) используют критерий Фишера, расчетное значение которого определяем по формуле
 (9)
(9)
где S2(1) – средняя дисперсия или дисперсия воспроизводимости, определяемая но формуле (4);
S2(2) – дисперсия, характеризующая рассеивание средних экспериментальных значений уu относительно прямой линии, определяемой по формуле (8) (дисперсия адекватности).
Дисперсия S2(2) характеризует точность аппроксимации зависимости ỹ=f(X) прямой линией, ее определяют по формуле
![]() (10)
(10)
где ![]() и
и ![]() экспериментальное и расчетное значения выходного параметра.
экспериментальное и расчетное значения выходного параметра.
После этого определяют число степеней свободы дисперсии адекватности
F{S2(2)}=N-2=28 (11)
Далее подставляем в формулу (9) значения дисперсии S2(1){y} и S2(2){y} рассчитывают критерий Фишера. Fp сравниваем с табличным значением критерия Фишера FT, которое определяют из [1.4] при доверительной вероятности α=0,95 и число степеней свободы f {S2(2)} и f { S2(1)}
FT=2.38, а Fр = 0.029
Fр < FT
Т.к. Fр < FT, то линейное уравнение адекватно.
Расчет суммы в формуле (10) сводим в табл. 3. Расчетные значения выходного параметра ![]() определяем из уравнения (8), подставляя значения Хu.
определяем из уравнения (8), подставляя значения Хu.
Таблица 3
Расчёт дисперсии адекватности
| u | xu | d1xu | YRu | ỹu | ỹu- YRu | (ỹu- YRu)2 |
| 1. | 4 | -7.864×10-3 | 9.492 | 9.70 | 0.208 | 0.043 |
| 2. | 12 | -0.024 | 9.477 | 9.56 | 0.083 | 6.950×10-3 |
| 3. | 20 | -0.039 | 9.461 | 9.48 | 0.019 | 3.645×10-4 |
| 4. | 27 | -0.053 | 9.447 | 9.45 | 2.853× 10-3 | 8.140×10-6 |
| 5. | 35 | -0.069 | 9.431 | 9.42 | -0.011 | 1.304×10-4 |
| 6. | 43 | -0.085 | 9.416 | 9.39 | -0.026 | 6.601×10-4 |
| 7. | 50 | -0.098 | 9.402 | 9.37 | -0.032 | 1.020×10-3 |
| 8. | 58 | -0.114 | 9.386 | 9.34 | -0.046 | 2.135×10-3 |
| 9. | 66 | -0.130 | 9.370 | 9.32 | -0.050 | 2.548×10-3 |
| 10. | 73 | -0.144 | 9.357 | 9.32 | -0.037 | 1.348×10-3 |
| 11. | 81 | -0.159 | 9.341 | 9.30 | -0.041 | 1.680×10-3 |
| 12. | 88 | -0.173 | 9.327 | 9.29 | -0.037 | 1.386×10-3 |
| 13. | 96 | -0.189 | 9.312 | 9.27 | -0.042 | 1.722×10-3 |
| 14. | 104 | -0.204 | 9.296 | 9.26 | -0.036 | 1.280×10-3 |
| 15. | 111 | -0.218 | 9.282 | 9.24 | -0.042 | 1.765×10-3 |
| 16. | 119 | -0.234 | 9.266 | 9.23 | -0.036 | 1.317×10-3 |
| 17. | 126 | -0.248 | 9.253 | 9.22 | -0.033 | 1.058×10-3 |
| 18. | 134 | -0.263 | 9.237 | 9.21 | -0.027 | 7.180×10-4 |
| 19. | 141 | -0.277 | 9.223 | 9.21 | -0.013 | 1.699×10-4 |
| 20. | 149 | -0.293 | 9.207 | 9.20 | -7.308×10-3 | 5.340×10-5 |
| 21. | 156 | -0.307 | 9.194 | 9.18 | -0.014 | 1.835×10-4 |
| 22. | 164 | -0.322 | 9.178 | 9.18 | 2.181×10-3 | 4.756×10-6 |
| 23. | 171 | -0.336 | 9.164 | 9.17 | 5.942×10-3 | 3.531×10-5 |
| 24. | 179 | -0.352 | 9.148 | 9.15 | 1.669×10-3 | 2.786×10-6 |
| 25. | 186 | -0.366 | 9.135 | 9.14 | 5.430×10-3 | 2.949×10-5 |
| 26. | 194 | -0.381 | 9.119 | 9.14 | 0.021 | 4.476×10-4 |
| 27. | 201 | -0.395 | 9.105 | 9.13 | 0.025 | 6.210×10-4 |
| 28. | 209 | -0.411 | 9.089 | 9.13 | 0.041 | 1.652×10-3 |
| 29. | 216 | -0.425 | 9.076 | 9.13 | 0.054 | 2.960×10-3 |
| 30. | 224 | -0.440 | 9.060 | 9.12 | 0.060 | 3.616×10-3 |
Похожие работы
... Но, дешевые товары не всегда имеют пониженное качество. Ряд товаров повседневного спроса устанавливаются определенное ограничение цен или торговых надбавок. Б (4/1) Классификация как метод товароведения: иерархический, фасетный методы классификации, правила классификации. Классификация - разделения множества объектов на подмножества по сходству или различию в соответствии с принятыми методами. ...
0 комментариев