Навигация
Определение коэффициентов уравнения регрессии
2.1. Определение коэффициентов уравнения регрессии
2.1.1 Свободный член уравнения определяем по формуле:
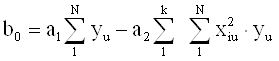
![]()
где yu- среднее экспериментальное значение в каждом u-том опыте;
x - кодированное значение уровня k-го фактора в u-том опыте;
k - количество факторов;
а1, а2 - числовые константы, берутся из таблицы.
| Число факторов (k) | Число опытов | Коэффициенты | ||||||
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | ||
| 2 | 13 | 0,200 | 0,100 | 0,125 | 0,250 | 0,125 | 0,0187 | 0,100 |
| 3 | 20 | 0,1663 | 0,0568 | 0,0732 | 0,1250 | 0,0625 | 0,0069 | 0,0568 |
| 4 | 31 | 0,1428 | 0,0357 | 0,0417 | 0,0625 | 0,0312 | 0,0037 | 0,0357 |
| 5 | 32 | 0,1591 | 0,0341 | 0,0417 | 0,0625 | 0,0312 | 0,0028 | 0,0341 |
2.1.2 Линейные коэффициенты определяем по формуле:
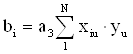
![]()
![]()
2.1.3. Коэффициенты парного взаимодействия:
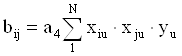
![]()
где xiu, xju-кодированные значения уровней i-го и j-го факторов соответственно и в u-том опыте.
2.1.4 Коэффициенты при квадратичных членах уравнения регрессии определяют:

![]()
![]()
После вычисления коэффициентов уравнения регрессии переходят к оценке их значимости.![]()
2.2. Оценка значимости коэффициентов уравнения регрессии.
2.2.1 Определяем дисперсию воспроизводимости S2{y} по формуле (дублирование опытов проводится только в нулевой точке).
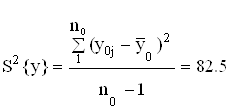
где n0 = 5 – число опытов в нулевой точке;
![]() = 252 – средний результат в нулевой точке;
= 252 – средний результат в нулевой точке;
y0j - каждый отдельный результат в нулевой точке.
2.2.2 Дисперсию (среднеквадратическую ошибку) в определении коэффициентов определяют для свободного члена:
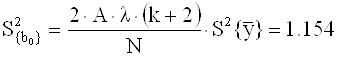
для линейных коэффициентов:
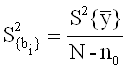
![]()
для коэффициентов парного взаимодействия:
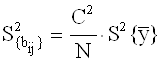
![]()
для квадратичных коэффициентов:
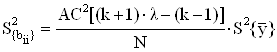
![]()
![]()
Формулы для подсчёта постоянных С, А, λ приведены ниже:
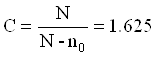

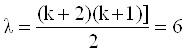
где N – общее число опытов;
k – число факторов в эксперименте.
Похожие работы
... Но, дешевые товары не всегда имеют пониженное качество. Ряд товаров повседневного спроса устанавливаются определенное ограничение цен или торговых надбавок. Б (4/1) Классификация как метод товароведения: иерархический, фасетный методы классификации, правила классификации. Классификация - разделения множества объектов на подмножества по сходству или различию в соответствии с принятыми методами. ...
0 комментариев