Навигация
Методика расчета энергосиловых параметров прокатки
7. Методика расчета энергосиловых параметров прокатки
Расчет энергосиловых параметров выполним по ходу прокатки. Для начала выполним расчет коэффициентов вытяжки и скоростного режима прокатки [3].
Площадь полосы в калибре определим по:
ω = В×d + 2 ((ao + bo) ho/2 + (aз + bз) hз/2) мм2, (1)
где В-ширина калибра;
d – толщина стенки калибра;
ao – толщина открытого фланца у вершины калибра;
bo – толщина открытого фланца у основания калибра;
ho – высота открытого фланца;
aз – толщина закрытого фланца у вершины калибра;
bз – толщина закрытого фланца у основания калибра;
hз – высота закрытого фланца.
Для расчета скоростного режима и энергосиловых параметров прокатки фасонные полосы пересчитываем на соответственные прямоугольные по методу приведенной высоты:
Нс = ω/В мм, (2)
где ω – площадь полосы в калибре;
В-ширина калибра.
Определим катающие диаметры валков. Расчет следует вести при максимальных диаметрах валков, чтобы определить максимальную энергосиловую загрузку оборудования стана.
Dк = D0 – Нс мм, (3)
где D0 – максимальный диаметр бочки валков (см. табл. 2.1);
Нс – приведенная высота фасонной полосы.
Коэффициент вытяжки в разрезном калибре:
λi = ωi-1/ ωi, (4)
где ωi-1 – площадь полосы задаваемой в калибр;
ωi – площадь полосы выходящей из калибра.
Конечную скорость прокатки определим, исходя из максимально допустимой скорости валков в чистовой клети с учетом запаса на регулирование в связи с переточкой валков в размере 8%:
![]() м/с, (5)
м/с, (5)
где Dк – катающий диаметр валков;
n – максимальная чистота вращения валков;
k – коэффициент запаса на регулирование в связи с переточкой валков.
Частота вращения валков:
![]() об/мин, (6)
об/мин, (6)
где V – скорость вращения валков;
Dк – катающий диаметр.
Найденную частоту вращения валков нужно сравнить с допустимой (см. табл. 2.1).
Найдем скорости в остальных калибрах из условия постоянства секундных объемов металла, проходящих через калибры этих клетей:
![]() м/с, (7)
м/с, (7)
где V – скорость вращения валков;
λ – коэффициент вытяжки.
Выполняем расчет энергосиловых параметров. Определим значения усилия, крутящие моменты и температурный режим прокатки.
Определим абсолютное изменение приведенной высоты:
ΔНс = (Н0с – Н1с) мм. (8)
Определим среднее значение приведенных высот в калибре:
Нср = (Н0с + Н1с)/2 мм, (9)
где Н0с – приведенная высота в предыдущем калибре;
Н1с – приведенная высота в данном калибре.
Относительное обжатие:
![]() , (10)
, (10)
где ΔН1 – абсолютное изменение приведенной высоты;
Н0с – приведенная высота в предыдущем калибре.
Скорость деформации металла:
![]() с-1, (11)
с-1, (11)
где n – частота вращения валков;
ε – относительное обжатие;
Dк – катающий диаметр;
Нс – приведенная высота в калибре.
Длина очага деформации:
![]() мм. (12)
мм. (12)
Рассчитаем контактную площадь прокатки:
F1 = 0.5×(B0 + B1)×lc мм2, (13)
где B0 – ширина раската перед входом в данный калибр;
B1 – ширина раската;
lc – длина очага деформации.
Найдем длину раската по проходам. При длине исходной заготовки 5 метров из описания технологии прокатки на данном стане.
Длины раската по проходам:
Li = Li-1×λi мм, (14)
где Li-1 – длина предыдущего раската;
λi – коэффициент вытяжки.
Определим сопротивление деформации стали 70 по методу термомеханических коэффициентов В.И. Зюзина:
σ = σод×Кt×Кε×Кu МПа, (15)
где σод – базисное значение сопротивления деформации, определяемое для данной марки стали при t = 1000 0C, ε = 0,1 и u = 10 с-1;
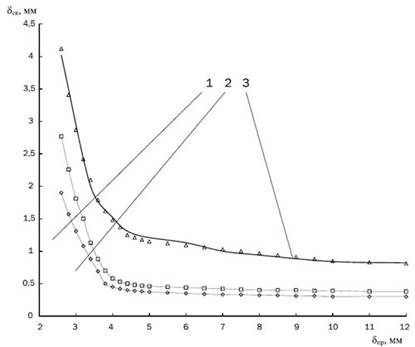
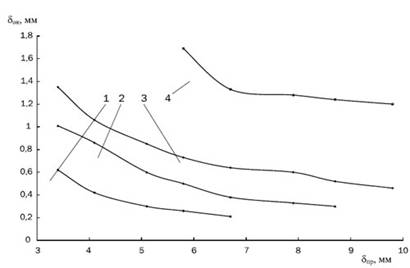
Кt, Кε, Кu – термомеханические коэффициенты, учитывающие соответственно влияние температуры прокатываемого металла, степени и скорости деформации. Эти коэффициенты определяются по формулам или кривым, построенным для каждой марки стали. В нашем случае для стали 10 пс определим эти коэффициенты по рисункам 7.1 и 7.2.
Рис. 7.1. Температурный Кt и степенной Кε коэффициенты стали 20ПС
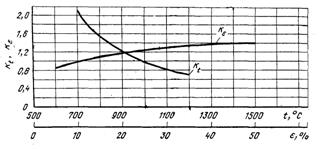
Рис. 7.2. Скоростной Кu коэффициент стали 20ПС
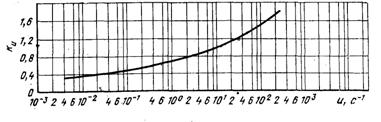
Для стали 20 пс σод = 82,32 МПа. [12]
Определяем температуру раската перед входом во вторую клеть. Для этого рассчитаем время охлаждения раската, которое складывается из паузы на передачу раската от одной клети к другой и машинного времени прокатки.
Рассчитаем время охлаждения раската:
![]() сек, (16)
сек, (16)
где Lp – длина рольганга;
Vр – скорость рольганга;
L1 – длина раската;
Lш – длина шлепера;
Vш – скорость шлепера;
V1 – скорость прокатки в данной клети.
Найдем повышение температуры металла вследствие перехода механической энергии деформации в теплоту:
Δtд = 0,183×σ×lnλ 0C, (17)
где σ – сопротивление деформации стали;
λ – коэффициент вытяжки.
Рассчитаем периметр поперечного сечения раската после прохода:
П = 2×(Нс + В) мм, (18)
где Нс – приведенная высота в калибре;
B – ширина раската.
Тогда на основе использования метода А.И. Целикова изменение температуры раската за время прокатки в калибре и перемещения к следующему калибру составит:
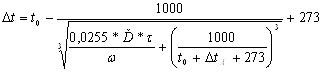 0С, (19)
0С, (19)
где t0 – температура раската перед входом в рассматриваемый калибр;
П – периметр поперечного сечения раската после прохода;
τ – время охлаждения раската;
ω – площадь поперечного сечения раската после прохода;
Δtд – повышение температуры металла вследствие перехода механической энергии деформации в теплоту.
Температура металла перед заходом в следующую клеть:
ti = ti-1 – Δt 0С, (20)
где ti-1 – температура прокатки в предшествующей клети;
Δt – изменение температуры раската за время прокатки в калибре и перемещения к следующему калибру составит.
Рассчитаем контактное давление прокатки по методу В.С. Смирнова:
р = 1,08×nσ×nж×nф×σ МПа, (21)
где nσ – коэффициент напряженного состояния, учитывающий влияние на контактное давление внешнего трения;
nж – коэффициент, учитывающий влияние внешних зон по отношению к геометрическому очагу деформации;
nф – коэффициент формы профиля.
Найдем коэффициент напряженного состояния:
nσ = ![]() , (22)
, (22)
где δ – коэффициент учитывающий влияние контактного трения на форму очага деформации;
ε – относительное обжатие.
Определим коэффициент учитывающий влияние контактного трения на форму очага деформации:
![]() , (23)
, (23)
где μ – коэффициент внешнего трения;
lc – длина очага деформации;
ΔНс – абсолютное изменение приведенной высоты.
Коэффициент внешнего трения:
μ = 0,55 – 0,00024×t, (24)
где t – температура деформируемого металла.
Найдем отношение длины очага деформации к среднему значению приведенной высоты: ![]() .
.
Определим значение коэффициента, учитывающего влияние внешних зон по отношению к геометрическому очагу деформации:
nж = ![]() , (25)
, (25)
где ![]() – фактор формы очага деформации.
– фактор формы очага деформации.
Найдем коэффициент формы профиля:
nф = ![]() , (26)
, (26)
где lc – длина очага деформации;
μ – коэффициент внешнего трения;
ΔНс – абсолютное изменение приведенной высоты.
Рассчитаем усилие прокатки:
Р = р×F×10-6 МН, (27)
где р – контактное давление прокатки;
F – контактная площадь прокатки.
Определим коэффициент плеча приложения усилия прокатки по формуле М.А. Зайкова – Н.А. Федорова:
φп = 5,85 – 11∙![]() + 7,35∙
+ 7,35∙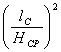 – 1,58∙
– 1,58∙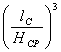 , (28)
, (28)
где ![]() – фактор формы очага деформации.
– фактор формы очага деформации.
Рассчитаем крутящий момент деформации:
Мвал = 2×Р×lc× φп кН×м, (29)
Ограничения по скоростному режиму прокатки проверяем по формулам (26) и (27) с учетом коэффициента загрузки электродвигателей стана.
Коэффициент загрузки электродвигателей стана по усилию прокатки:
![]() , (30)
, (30)
где Р – усилие прокатки;
Рmax – максимально допустимое усилие прокатки.
![]() м/с; (31)
м/с; (31)
![]() м/с, (32)
м/с, (32)
где Dк – катающий диаметр;
nmax, nmax – соответственно максимально возможные и минимальные частоты вращения валков (см. табл. 2.1);
k – коэффициент загрузки электродвигателей стана.
Определим часовую производительность стана:
![]() , (33)
, (33)
где G – масса заготовки;
Тт – такт прокатки;
Ки – коэффициент использования;
Принимаем Ки = 095.
Похожие работы
... конструкциях металл следует применять лишь в тех случаях, когда замена его другими видами материалов (в первую очередь железобетоном) нерациональна. Транспортабельность. В связи с изготовлением металлических конструкций, как правило, на заводах с последующей перевозкой на место строительства в проекте должна быть предусмотрена возможность перевозки их целиком пли по частям (отправочными ...
... исходными материалами и продуктами производства, которые и создают основные предпосылки для проектирования промышленных зданий, которые идеально впишутся в своеобразные решения планировки территори, их застройки и архитектурно-пространственной композиции. ПРОИЗВОДСТВЕННЫЕ ЗДАНИЯ ИЗ ЛЕГКИХ МЕТАЛЛИЧЕСКИХ КОНСТРУКЦИЙ ТИПА КАНСК Стальные рамные конструкции из прокатных широкополочных и сварных ...
... геометрией и пожарной нагрузкой с целью минимизации затрат на огнезащиту. Математическая модель расчета огнестойкости металлических строительных конструкций. Для определения температур внутри стенки металлических конструкций с нанесенным огнезащитным вспучивающимся покрытием решается уравнение теплопроводности: где ρ – плотность материала конс трукции; с – удельная теплоемкость материала ...
... , асбестоцементных, полимерных, рулонных кровельных и гидроизоляционных материалов и строительного стекла 2. Строительные конструкции Номенклатура показателей качества каменных и армокаменных, бетонных и железобетонных, металлических, асбестоцементных и деревянных конструкций 3. Инженерное оборудование зданий и сооружений Номенклатура показателей качества санитарно-технического ...
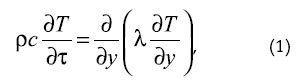
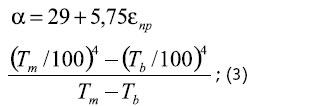
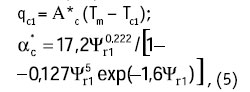
0 комментариев