Навигация
Проверяем рабочие контактные напряжения по формуле
1. Проверяем рабочие контактные напряжения по формуле
σН = ZН · ZМ · ZЕ· 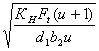 < σНР , (26)
< σНР , (26)
где ZН – коэффициент, учитывающий форму сопряженных поверхностей зубьев (ZН = 1,76 по [3, табл. 3]);
ZМ – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес (ZМ = 274 · 103 Па1/2 по [3, табл. П22]);
ZЕ – коэффициент, учитывающий суммарную длину контактных линий;
КН – коэффициент нагрузки;
Ft– окружная сила, Н;
u – передаточное число;
d – делительный диаметр шестерни, мм;
b – ширина венца зубчатого колеса, мм;
σНР – допускаемое контактное напряжение, МПа (σНР = 420МПа).
Согласно [3, стр.96] коэффициент ZЕ, учитывающий суммарную длину контактных линий, определяется по формуле
ZЕ = ![]() , (27)
, (27)
где Еα – коэффициент торцового перекрытия, определяется по формуле
Еα = [1,88 – 3,2∙ (1/ z1 + 1/ z2)] ∙ cosβ, (28)
где z1 – число зубьев шестерни;
z2 – число зубьев зубчатого колеса.
Подставляем числовые значения в формулу (28) и определяем коэффициент торцового перекрытия
Еα = [1,88 – 3,2∙ (1/ 46 +1/ 74)] ∙ cos0○ = 1,77.
Подставляем значение коэффициента торцового перекрытия в формулу (27)
ZЕ = ![]() = 0,86
= 0,86
Коэффициент нагрузки определяем по формуле
KH = KHβ· KHυ, (29)
где KHβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (KHβ = 1,02 по [3, табл. П25]);
KHυ – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении (KHυ = 1,13 по [3, табл. П26]).
Подставляем коэффициенты KHυ, KHβ в формулу (29) и находим коэффициент нагрузки
KH = 1,02 · 1,13 = 1,15.
По формуле (26) проверяем контактную выносливость зубьев:
σН = 1,76·274·103·0, 86· = 393·106 Па < σНР = 420Мпа.
= 393·106 Па < σНР = 420Мпа.
2. Проводим проверочный расчет зубьев на их выносливость при изгибе. Согласно рекомендациям [3, с. 307], выносливость зубьев по напряжениям изгиба
проверим по уравнению
σF = ![]() < σFР (30)
< σFР (30)
где YF – коэффициент формы зубьев;
KF – коэффициент нагрузки;
Ft– окружная сила, Н;
b – ширина венца зубчатого колеса, мм;
mn – нормальный модуль, мм;
σFP – допускаемое напряжение при расчете на выносливость зубьев при изгибе, Мпа.
(σFP =110 Мпа).
Коэффициент нагрузки определяем по формуле
KF = KFβ· KFυ (31)
где KFβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (KFβ = 1,04 по [3, табл. П25]);
KFυ – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении; для прямозубых колес (KFυ = 1,26 по [3, табл.П26];
Следовательно, подставляем коэффициенты KFυ, KFβ в формулу (31) и находим коэффициент нагрузки
KF = 1,04 · 1,26= 1,31.
Согласно рекомендациям [3, с. 110], вычисляем эквивалентные числа зубьев шестерни и колеса по формуле
zυ= z/cos3β, (32)
где z – число зубьев шестерни (z1) или колеса (z2);
β – угол наклона линии зуба.
Тогда по формуле (34) получаем
z′υ= 46/cos3(0) = 46;
z′′υ= 74/ cos3(0) = 74.
Согласно рекомендациям [3, табл. П27], интерполируя, определяем коэффициент формы зуба шестерни Y′F = 3,52 при z′υ = 46 и колеса Y′′F = 3,72
при z′′υ= 74.
Сравнительная оценка прочности зуба шестерни и колеса при изгибе:
σ′FP/Y′F = 130/3,52 = 36,9 МПа,
σ′′FP/ Y′′F = 110/3,72 = 29,56 МПа.
Прочность зубьев колеса оказалась ниже, чем зубьев шестерни, поэтому проверку на выносливость по напряжениям изгиба следует выполнить для зубьев колеса.
По формуле (30) проверяем выносливость зубьев при изгибе:
σF = ![]() =
= ![]() 108 МПа < σFP = 110 МПа.
108 МПа < σFP = 110 МПа.
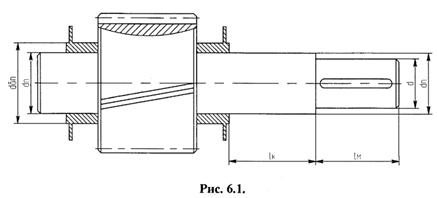
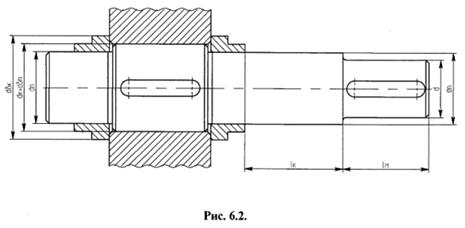
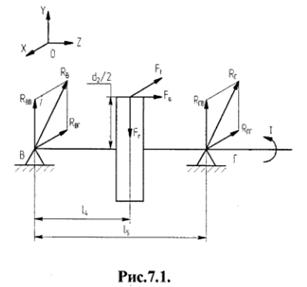
Диаметр выходного конца вала определим грубо приближенно (ориентировочный расчет) из расчета на прочность при кручении по заниженным допускаемым касательным напряжениям: [τК] = 20…40 МПа. Согласно рекомендациям [3, с. 307], принимаем [τК]' = 25 МПа для стали 45 (при df1 = 65,25мм целесообразно изготовить быстроходный вал вместе с шестерней) и [τК]'' = 20 МПа для стали 35, которую назначаем для изготовления тихоходного вала.
Похожие работы
... напряжения σэкв = 1, 3 Fр / А (109) σэкв = 1, 3 *1780, 08 / 84, 2 = 27, 48 Н/мм2 [σ] 27, 48 75 Проверить прочность стяжных винтов подшипниковых узлов быстроходного вала цилиндрического редуктора. Rу – большая из реакций в вертикальной плоскости в опорах подшипников быстроходного вала, Rу = 2256, 08 Н. Диаметр винта d2 = 12 мм, шаг резьбы Р = 1, 75 мм. Класс прочности 5.6 ...
... с синхронной частотой вращения 750 об/мин. 2. Кинематический и энергетический расчёт привода 2.1 Кинематический расчёт Требуемое передаточное число привода при принятом электродвигателе: Разобьём передаточное число привода между редуктором и ремённой передачей. Примем: передаточное число ремённой передачи ирп = 3,55, тогда передаточное число редуктора: Частота вращения ...
Определяем действительное передаточное число привода u0 по формуле 3.8[1] (7) Рассчитываем действительное передаточное число открытой цилиндрической передачи u89 (8) Нагрузочные характеристики каждого из валов привода (мощность Pj, частота вращения nj, крутящий момент Tj) приведены в таблице 1.1, заполненной на основании таблицы 1.2.6.[2]. Таблица 1.1 – Силовые и ...
... 1.6 Задаёмся передаточным отношением открытой передачи u = 2¸ 3 1.7 Определяем передаточное отношение редуктора Передаточное отношение редуктора должно входить в промежуток для конической прямозубой передачи U=2¸ 3 , где U - передаточное отношение двигателя Uоп - передаточное отношение открытой передачи ...
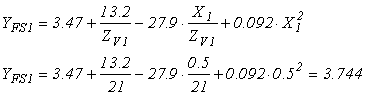
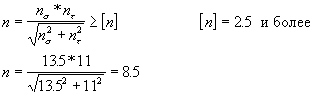
0 комментариев