Навигация
Вычисляем наибольшие напряжения изгиба и кручения для опасного сечения С. Суммарный изгибающий момент по [3, с. 311], определяется по формуле
4. Вычисляем наибольшие напряжения изгиба и кручения для опасного сечения С. Суммарный изгибающий момент по [3, с. 311], определяется по формуле
МИ = ![]() , (78)
, (78)
где МFr и MFt – изгибающие моменты, Н ∙ м.
Тогда
МИ = ![]() = 20,2 Н∙м.
= 20,2 Н∙м.
Напряжение изгиба по [3, с. 311], определяется по формуле
σИ = МИ/WX = 32 МИ/(πdf13), (79)
где МИ – суммарный изгибающий момент, Н∙м;
WX – осевой момент сопротивления круглого сечения вала, м3;
WX = πdf13/32, (80)
df1 – диаметр впадин шестерни, мм.
Подставив известные величины в формулы (79) и (80) получим
σИ = 32 МИ/(πdf13) = 32·20,2 / (3,14· (65,25·10-3)3) = 0,74·106 Па.
Допускаемое касательное напряжение на кручение определяется по формуле
τК = Т/ WР, (81)
где Т – крутящий момент, Н∙м;
WР – полярный момент сопротивления круглого сечения вала, м3;
WР = πdf13/16 (82)
df1 – диаметр впадин шестерни, мм.
Подставив известные величины в формулы (81) и (82) получим
τК = 16·41,8 / (3,14· (65,25·10-3)3) = 0,77·106 Па.
5. Согласно рекомендациям [3, с. 194], определяем эквивалентное напряжение по гипотезе наибольших касательных напряжений:
σЭ = ![]() ≤ [σИ]-1, (83)
≤ [σИ]-1, (83)
где σИ – напряжение изгиба, Па;
τК – касательное напряжение на кручение, Па;
[σИ]-1 – допускаемое напряжение, МПа.
Тогда
σЭ = ![]() = 1,7 МПа,
= 1,7 МПа,
что значительно меньше [σИ]-1 = 62,1 МПа.
Тихоходный вал.
1. Материал для изготовления тихоходного вала – сталь 35 , для которой по [3, табл. П3] при d < 100 мм предел прочности σВ = 510 МПа.
Предел выносливости, согласно рекомендациям [3, с.195] определяется по формуле
σ-1 = 0,43σВ, (84)
σВ – предел прочности, МПа.
Тогда по формуле (84) предел выносливости
σ-1 = 0,43 ∙510 = 219МПа.
2. Допускаемое напряжение изгиба при симметричном цикле напряжений, согласно рекомендациям [3, с. 195], определяется по формуле
[σИ]-1 = [σ-1 / ([n]Kσ] kРИ, (85)
где σ-1 – предел выносливости, МПа;
n – коэффициент запаса прочности (n = 2,2);
Kσ – эффективный коэффициент концентрации напряжений (Kσ = 2,2 по [3, с. 310]); kРИ – коэффициент режима нагрузки при расчете на изгиб (kРИ = 1 по [3, с. 310]).
Тогда по формуле (85) получаем
[σИ]-1 = [219/(2,2 ∙ 2,2)] ∙1 = 45,25 МПа.
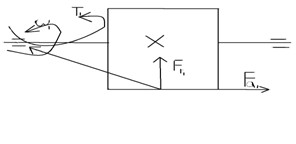
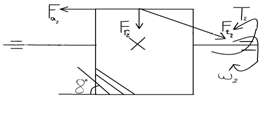
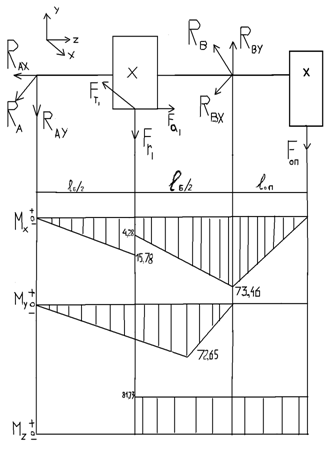
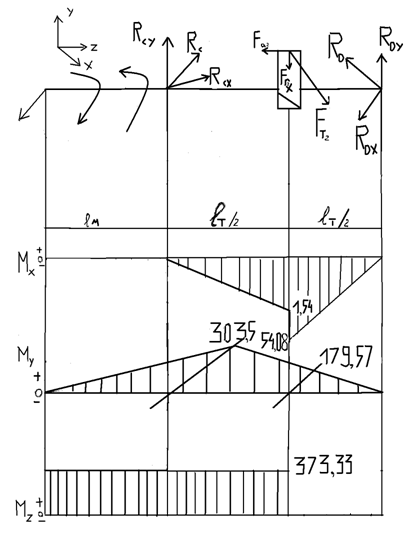
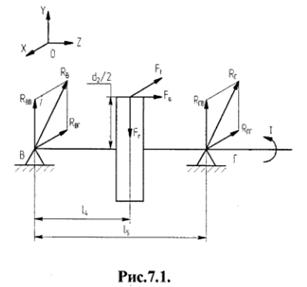
3. Вычерчиваем схему нагружения вала и строим эпюры изгибающих и крутящих моментов (рис. 3.):
а) определяем реакции опор в вертикальной плоскости yOz от сил Fr и Fа
∑МА = – Fr a2 – Fa0,5d2 + YB·2 a2 = 0, (86)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Fr – радиальная сила, сжимающая зуб, Н;
Fa – осевая сила, Н.
Тогда из уравнения (86) следует, что
YB = ![]() (87)
(87)
Подставив известные величины в формулу (87) получим
YB = ![]() = 200 Н
= 200 Н
∑МВ = – YА·2 a2 – Fa0,5d2 + Fr a2 = 0, (88)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Fr – радиальная сила, сжимающая зуб, Н; Fa – осевая сила, Н.
Выразив из уравнения (88) YА получим
YА = ![]() (89)
(89)
Подставив известные величины в формулу (89) получим
YА = ![]() = 200 Н.
= 200 Н.
б) определяем реакции опор в горизонтальной плоскости xOz от силы Ft:
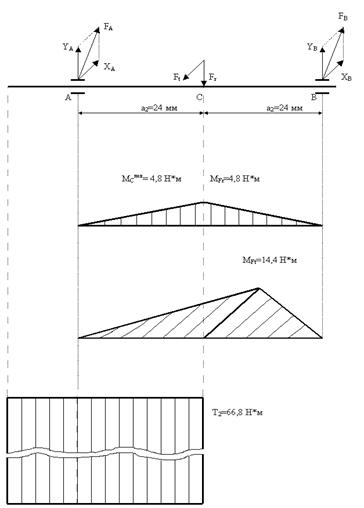
Рис. 3.
∑МА = – Ft a2 + ХB·2 a2 = 0, (90)
a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Ft – окружная сила, изгибающая зуб, Н.
Выразив из уравнения (90) ХВ получаем
ХВ = Ft a2/2 a2 (91)
Подставив известные величины в формулу (91) получим
ХВ = 1200/2 = 600 Н,
ХА = ХВ = 600 Н;
в) для построения эпюр определяем размер изгибающих моментов в характерных точках (сечениях) А, С и В;
в плоскости yOz
МА = МВ = 0; (92)
МСЛЕВ = YА· a2, (93)
МСПРАВ = YВ· a2, (94)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
YА , YВ – опорные реакции, Н.
Тогда по формуле (93) получаем
МСЛЕВ = 200 ∙ 0,024 = 4,8 Н ∙ м;
По формуле (94) имеем
МСПРАВ = 200 · 0,024 = 4,8 Н ∙ м;
(МFrFa)max = 4,8 Н ∙ м;
в плоскости хOz
МА = МВ = 0; (95)
МС = ХА· a2, (96)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
ХА – опрная реакция, Н.
Тогда по формуле (96) получаем
МС = 600 · 0,024 = 14,4 Н ∙ м;
МFt = 14,4 Н ∙ м;
г) крутящий момент Т = Т2 = 66,8 Н∙м;
д) выбираем коэффициент масштаба и строим эпюры (рис. 3.).
4. Вычисляем наибольшие напряжения изгиба и кручения для опасного сечения С. Суммарный изгибающий момент, согласно рекомендациям [3, с. 311], определяется по формуле
МИ = ![]() , (97)
, (97)
где МFrFaи MFt – изгибающие моменты, Н ∙ м.
Подставляем значения изгибающих моментов в формулу (97) получаем
МИ = ![]() = 15,1Н∙м.
= 15,1Н∙м.
Диаметр вала в опасном сечении d2''' = 38 мм ослаблен шпоночной канавкой. Поэтому в расчет вводим значение d, меньшее на 8…10% d2'''. Принимаем расчетный диаметр вала в опасном сечении d = 35 мм.
Напряжение изгиба по [3, с. 311], определяется по формуле
σИ = МИ/WX (98)
где МИ – суммарный изгибающий момент, Н•м;
WX – осевой момент сопротивления круглого сечения вала, м3
WX - расчетный диаметр вала в сечении С, мм.
WX = πd 3/32, d (99)
Тогда подставляя значения суммарного изгибающего момента и расчетного диаметра вала в формулу (98) и (99) получаем
σИ = 32·15,1∙103/ (3,14∙ (35)3) = 3,58 МПа.
Допускаемое касательное напряжение на кручение определяется по формуле
τК = Т / WР, (100)
где Т – крутящий момент, Н∙м;
WР – полярный момент сопротивления круглого сечения вала, м3;
WР = πd3/16 (101)
d – расчетный диаметр вала в сечении С, мм.
Тогда подставляя значения крутящего момента и расчетного диамера вала в формулы (100) и (101) получаем
τК = 16·66,8·103/ (3,14· (35)3) = 7,9 МПа.
5. Согласно рекомендациям [3, с. 194], определяем эквивалентное напряжение по гипотезе наибольших касательных напряжений и сравниваем его значение с допускаемым:
σЭ = ![]() ≤ [σИ]-1, (102)
≤ [σИ]-1, (102)
где σИ – напряжение изгиба, Па;
τК – касательное напряжение на кручение, Па;
[σИ]-1 – допускаемое напряжение, МПа.
Тогда по формуле (102) получаем
σЭ = ![]() = 16,2 МПа,
= 16,2 МПа,
что значительно меньше [σИ]-1 = 45,25 МПа.
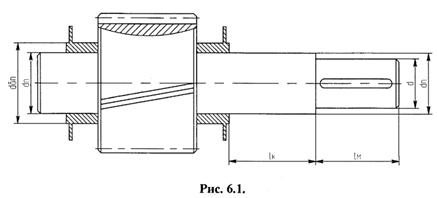
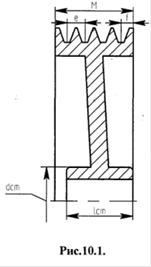
2.11 Второй этап эскизной компоновки редуктораЗадача второго этапа компоновки – конструктивно оформить механизм редуктора (шестерню, зубчатое колесо, валы, корпус, подшипники) для последующей проверки прочности валов и других деталей (рис.П.1.2). Вычерчивание производится в одной проекции (разрез по осям валов при снятой крышке редуктора в масштабе 1:2).
1. Оформляем конструкции шестерни и зубчатого колеса (разрез) по конструктивным размерам, найденным ранее.
2. Разрабатываем конструкцию узла ведущего вала:
а) оставив неизменным зазор y = 6 мм между торцом шестерни и внутренней стенкой корпуса, очерчиваем часть этой стенки, разрывая ее в соответсвующих местах на величину, равную наружному диаметру подшипников;
б) вычерчиваем подшипники в разрезе. Для экономии времени в разрезе вычерчиваем одну половину подшипника, а для второй наносим лишь габариты;
в) далее вычерчиваем вал, крышки подшипников и т.д.
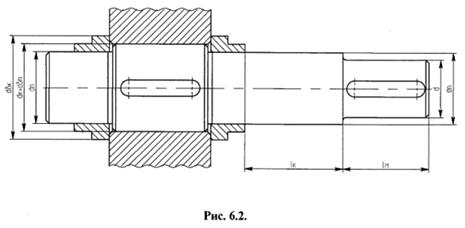
3. Разрабатываем конструкцию узла ведомого вала:
а) для фиксации зубчатого колеса от осевых перемещений предусматриваем утолщение вала с одной стороны и установку распорного кольца – с другой;
б) сохраняя намеченный в первом этапе компоновки зазор между торцом ступицы зубчатого колеса и внутренней стенкой корпуса, очерчиваем часть этой стенки, разрывая ее в соответсвующих местах на величину, равную наружному диаметру подшипников;
в) вычерчиваем вал, подшипники, крышки подшипников с болтами крепления крышек и.т.д.
2.12 Подбор шпонок и проверочный расчет шпоночных соединенийШпонки подбираем по таблицам ГОСТа в зависимости от диаметра вала и проверяем расчетом соединения на смятие.
Быстроходный вал. Для консольной части вала при dВ1 = 24 мм по [3, табл. П49] подбираем призматическую шпонку b × h = 8 × 7 мм. Длину шпонки принимаем из ряда стандартных длин так, чтобы она была меньше длины посадочного места вала l1 = 42 мм на 3…10 мм и находилась в границах предельных размеров длин шпонок.
Согласно рекомендациям [3, с 312], принимаем l = 36 мм – длина шпонки со
скругленными торцами. Расчетная длина шпонки определяется по формуле
lР = l – b, (103)
где l – длина шпонки, мм;
b – ширина шпонки, мм.
Тогда по формуле (103) получаем
lР = 36 – 8 = 28 мм.
Допускаемые напряжения смятия в предположении посадки полумуфты, изготовленной из стали, [σСМ] = 100…150 МПа.
Согласно рекомендациям [3, с. 234] вычисляем расчетное напряжение смятия по формуле
σСМ = 4,4Т1/(d lР h), (104)
где Т1 – крутящий момент, Н∙м;
d – диаметр вала, мм;
lР – расчетная длина шпонки, мм;
h – высота шпонки, мм.
Тогда подставляя значения крутящего момента, диаметра вала, длины и высоты шпонки в формулу (104) получаем
σСМ = 4,4Т1/(d lР h) = 4,4·41,8 / (24·28·7·10 –9) = 39 МПа < [σСМ].
Итак, принимаем шпонку 8×7×36 (СТ СЭВ 189 – 75).
Тихоходный вал. 1.Для выходного конца вала при dВ2 = 28 мм по [3, табл. П49] подбираем призматическую шпонку b × h = 8 × 7 мм. Длину шпонки принимаем из ряда стандартных длин так, чтобы она была меньше длины посадочного места вала l2 =48 мм на 3…10 мм и находилась в границах предельных размеров длин шпонок.
Согласно рекомендациям [3, с 312], принимаем l = 40 мм – длина шпонки со скругленными торцами. Расчетная длина шпонки определяется по формуле (103)
lР = 40 – 8 = 32 мм.
Допускаемые напряжения смятия в предположении посадки полумуфты, изготовленной из стали, [σСМ] = 100…150 МПа.
Согласно рекомендациям [3, с. 234] вычисляем расчетное напряжение смятия по формуле
σСМ = 4,4Т2/(d lР h), (105)
где Т2 – крутящий момент, Н∙м;
d – диаметр вала, мм;
lР – расчетная длина шпонки, мм;
h – высота шпонки, мм.
Тогда по формуле (108) имеем
σСМ = 4,4·66,8 / (28·32·7·10 –9) = 46,8 МПа < [σСМ].
Принимаем шпонку 8×7×40 (СТ СЭВ 189 – 75).
2. Для вала под ступицу зубчатого колеса при d2''' = 38 мм по [3, табл. П49] подбираем призматическую шпонку b × h = 10 × 8 мм. Так как lСТ = 36 мм, то принимаем длину призматической шпонки l = 30 мм со скругленными торцами. Расчетная длина шпонки определяется по формуле (103)
lР = 30 – 10 = 20 мм.
Допускаемые напряжения смятия в предположении посадки полумуфты, изготовленной из стали, [σСМ] = 100…150 МПа. Согласно рекомендациям [3, с. 234] вычисляем расчетное напряжение смятия по формуле (105)
σСМ = 4,4Т2/( d2'''lР h) d2'''= 4,4·66,8 / (38·20·8·10 –9) = 48,3 МПа < [σСМ].
Под ступицу колеса принимаем шпонку 10×8×30 (СТ СЭВ 189 – 75).
2.13 Подбор подшипниковПодшипники качения подбираем по таблицам ГОСТа в зависимости от размера и направления действующих на подшипник нагрузок; диаметра цапфы, на которую насаживается подшипник; характера нагрузки; угловой скорости вращающегося кольца подшипника; желательного срока службы подшипника и его наименьшей стоимости.
Быстроходный (ведущий) вал.
1 Определяем нагрузки, действующие на подшипники:
осевая сила
Fa = 0 Н;
определяем результирующие радиальные реакции подшипников, согласно рекомендациям [3, с. 313], по формулам
FrA = ![]() , (106)
, (106)
FrВ = ![]() , (107)
, (107)
где XA и YA – опорные реакции, Н.
Тогда по формулам (106) и (107) получаем
FrA = ![]() = 632 Н.
= 632 Н.
FrВ = ![]() = 632Н.
= 632Н.
2. Выбираем тип подшипников. Так как у нас отсутсвует осевая сила Fa ,а присутствует только радиальная, то следует применить родиальные роликоподшипники с кароткими цилиндрическими роликами [3, с. 208].
3. Согласно рекомендациям [3, с. 313], вычисляем требуемую динамическую грузоподъемность подшипника по формуле
СТР = (XVFr )KбKT(6·10 –5nLh)1/α, (108)
где X, Y – коэффициенты радиальной и осевой нагрузок соответственно;
Fr – фактическая радиальная нагрузка подшипника, Н;
Fа – осевая нагрузка подшипника, Н;
V – коэффициент вращения;
Kб – коэффициент безопасности, зависящий от типа механизма, в котором подшипник установлен;
KT – температурный коэффициент;
n – частота вращения, мин -1;
Lh – требуемая долговечность подшипника, ч;
α – величина, зависящая от формы кривой контактной усталости.
Принимаем: V = 1 по [3, табл. П45]; Kб = 1,2 по [3, табл. П46]; KT = 1 по [3, табл. П47]; согласно рекомендациям [3, с. 213], коэффициент радиальной нагрузки X = 1; для роликовых подшипников по [3, с. 214] α = 10/3; требуемая долговечность подшипников Lh = 20000 ч.
По формуле (108) вычисляем динамическую грузоподъемность подшипника:
СТР = (1·1·632)·1,2·1·(6·10-5·960·20·103)0,3= = 6285,4 Н = 6,3 кН.
Согласно рекомендациям [3, табл. П41], окончательно принимаем роликоподшипник 2206 легкой серии для которого d = 30 мм, D = 62, Тmax = 16 мм,
С = 16,9 кН., что >> СТР требуемой.
Тихоходный (ведомый) вал.
1 Определяем нагрузки, действующие на подшипники:
осевая сила
Fa = 0 Н;
определяем результирующие радиальные реакции подшипников, согласно рекомендациям [3, с. 313], по формулам (106) и (107)
FrA = ![]() = 632 Н.
= 632 Н.
FrВ = ![]() = 632 Н
= 632 Н
2. Выбираем тип подшипников. Так как у нас отсутсвует осевая сила Fa ,а присутствует только радиальная, то следует применить родиальные роликоподшипники с кароткими цылиндрическими роликами [3, с. 208].
3. Согласно рекомендациям [3, с. 313], вычисляем требуемую динамическую грузоподъемность подшипника по формуле (108).
Принимаем: V = 1 по [3, табл. П45]; Kб = 1,2 по [3, табл. П46]; KT = 1 по [3, табл. П47]; согласно рекомендациям [3, с. 213], коэффициент радиальной нагрузки X = 1; для роликовых подшипников по [3, с. 214] α = 10/3; требуемая долговечность подшипников Lh = 20000 ч.
По формуле (108) вычисляем динамическую грузоподъемность подшипника:
СТР = (1·1·632)·1,2·1·(6·10-5·600·20·103)0,3 = 15458,8 Н =5,4 кН.
Согласно рекомендациям [3, табл. П41], принимаем конический роликоподшипник 2207 легкой серии для которого d = 35 мм, D = 72, Тmax = 17 мм, С = 25 кН. ,что>> СТР требуемой.
2.14 Уточненный расчет валовОпределение коэффициентов запаса прочности производим для особо опасных сечений каждого из валов, принимая при этом, что нормальные напряжения изменяются по симметричному циклу, а касательные по пульсирующему.
Ведущий вал
Так как быстроходный вал изготовляют вместе с шестерней, то его материал известен – сталь 45, для которой предел выносливости σ-1 = 301 МПа.
Определяем предел выносливости при симметричном цикле кручения по формуле
τ-1 = 0,58 σ-1, (109)
где σ -1 – предел выносливости, МПа.
Тогда подставляя значение предела выносливости в формулу (109) получаем
τ-1= 0,58∙301 = 174,158МПа.
1. Рассмотрим сечение в точке А (рис.2). Считаем, что эта часть вала при передаче вращающего момента через муфту от электродвигателя работает только на кручение. Концентрацию напряжений вызывает наличие шпоночной канавки.
Коэффициент запаса прочности по касательным напряжениям определяется по формуле
n = nτ = 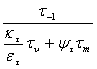 , (110)
, (110)
где τ-1 – предел выносливости при симметричном цикле кручения, МПа;
τυи τm – амплитуда и среднее напряжение цикла касательных напряжений;
ψτ – коэффициент, отражающий соотношения пределов выносливости при пульсирующем цикле кручения [ 2, с. 166];
κτ – коэффициент концентрации напряжения кручения [2,табл.8.5];
ετ – масштабный фактор для нормальных и касательных напряжений [2, табл. 8.1].
Амплитуда и среднее напряжение цикла касательных напряжений определяются по формуле
τυ= τm= Т1 / 2Wк нетто, (111)
где Т1 – крутящий момент, Н∙м;
Wк нетто – момент сопротивления кручению по сечению нетто, м3.
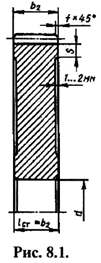
Момент сопротивления кручению по сечению нетто определяется по формуле
Wк нетто = ![]() , (112)
, (112)
где b – ширина шпоночной канавки, мм;
d – диаметр вала, мм;
t – глубина шпоночной канавки в ведущем вале, мм.
Тогда подставляя значения ширины, высоты шпоночной канавки и значение диаметра вала в формулу (112) получаем
Wк нетто = ![]() = 2,3·10 –6 м3.
= 2,3·10 –6 м3.
По формуле (111) определяем амплитуду и среднее напряжение цикла касательных напряжений
τυ= 41,8/(2·2,3·10-6) = 9,1 МПа.
Согласно рекомендациям [2, с.345], принимаем коэффициенты снижения пределов выносливости: ψτ = 0,1 по [2, с. 158]; ετ = 0,88 по [2, табл. 8.1]; κτ = 1,6 по [2, табл. 8.5].
Тогда по формуле (110) определяем коэффициент запаса прочности
n = nτ = 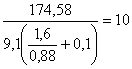
Ведомый вал.
Материал для изготовления тихоходного вала – сталь 35 , для которой предел выносливости σ-1 = 219МПа. Определяем предел выносливости при симметричном цикле кручения по формуле (109)
τ-1 = 0,58 σ-1 = 0,58·219 = 127 МПа.
Рассмотрим сечение в точке А (рис.3). В этом сечении возникает наибольший изгибающий момент. Концентрация напряжений в данном сечении обусловлена наличием шпоночной канавки.
1. Суммарный изгибающий момент МИ = 15,1 Н·м.
2. Определяем момент сопротивления сечения нетто по формуле
Wнетто = ![]() , (113)
, (113)
где b – ширина шпонки, мм;
d – диаметр вала, мм;
t – глубина шпоночной канавки, мм.
Тогда по формуле (113) получаем
Wнетто = ![]() 1,8·10-6 м3.
1,8·10-6 м3.
3. Амплитуда номинальных напряжений изгиба определяется по формуле
συ= σmax= МИ / Wнетто, (114)
где МИ – суммарный изгибающий момент, Н∙м; Wнетто – момент сопротивления сечения нетто, м3.
Тогда по формуле (114) получаем
συ= 15,1/1,8·10-6 = 8,39 МПа.
Похожие работы
... напряжения σэкв = 1, 3 Fр / А (109) σэкв = 1, 3 *1780, 08 / 84, 2 = 27, 48 Н/мм2 [σ] 27, 48 75 Проверить прочность стяжных винтов подшипниковых узлов быстроходного вала цилиндрического редуктора. Rу – большая из реакций в вертикальной плоскости в опорах подшипников быстроходного вала, Rу = 2256, 08 Н. Диаметр винта d2 = 12 мм, шаг резьбы Р = 1, 75 мм. Класс прочности 5.6 ...
... с синхронной частотой вращения 750 об/мин. 2. Кинематический и энергетический расчёт привода 2.1 Кинематический расчёт Требуемое передаточное число привода при принятом электродвигателе: Разобьём передаточное число привода между редуктором и ремённой передачей. Примем: передаточное число ремённой передачи ирп = 3,55, тогда передаточное число редуктора: Частота вращения ...
Определяем действительное передаточное число привода u0 по формуле 3.8[1] (7) Рассчитываем действительное передаточное число открытой цилиндрической передачи u89 (8) Нагрузочные характеристики каждого из валов привода (мощность Pj, частота вращения nj, крутящий момент Tj) приведены в таблице 1.1, заполненной на основании таблицы 1.2.6.[2]. Таблица 1.1 – Силовые и ...
... 1.6 Задаёмся передаточным отношением открытой передачи u = 2¸ 3 1.7 Определяем передаточное отношение редуктора Передаточное отношение редуктора должно входить в промежуток для конической прямозубой передачи U=2¸ 3 , где U - передаточное отношение двигателя Uоп - передаточное отношение открытой передачи ...
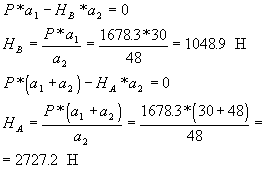
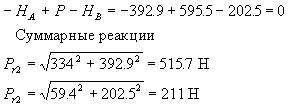
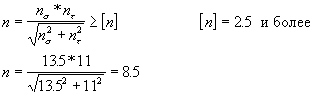
0 комментариев