Навигация
Преобразование произвольной системы сил
35662
знака
9
таблиц
28
изображений
1.7.2. Преобразование произвольной системы сил.
Применить правило параллелограмма сил непосредственно к произвольной системе сил нельзя, так как линии действия сил не пересекаются в одной точке. Предварительно систему сил приводят к одному центру на основании теоремы о параллельном переносе силы.
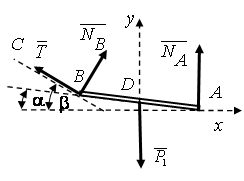
Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится (рис.1.22).
В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов - суммарным моментом. Суммарный вектор 
* называют главным вектором системы сил, суммарный момент 
*
- главным моментом системы сил.
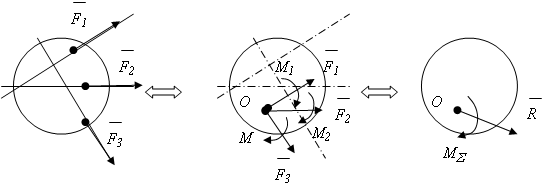
Рис.1.22
Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору * и главному моменту * системы сил.
Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат
, ( 1.8 )
. (1.9)
1.8 Условия равновесия систем сил
1.8.1. Равновесие системы сходящихся силПо определению (см.п.1.1) действие системы сходящихся сил эквивалентно действию одной равнодействующей силы 
. Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю 
= 0.
Из формулы (1.7) следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю
å Fkx = 0
å Fky = 0 ( 1.10) åFkz = 0
Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю
å Fkx = 0
å Fky = 0 ( 1.11 )
1.8.2. Равновесие произвольной системы сил.
Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия
* = 0 (1.12 )
* = 0
Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю.
åFkx = 0
åFky = 0
åFkz = 0 (1.13)
åМх (
k) = 0
åМy (k) = 0
åМz (k) = 0
Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю.
åFkx = 0
åFky = 0 (1.14)
åМо (k) = 0
1.9. Вопросы для самоконтроля по разделу
1. Дайте определение абсолютно твердого тела, материальной точки, силы, линии действия силы, системы сил (плоской, пространственной, сходящейся) произвольной систем сил.
2. Что называется проекцией силы на ось, на плоскость?
3. Что называется моментом силы, как определяется момент силы относительно точки?
4. Изменяется ли момент силы относительно данной точки при переносе силы вдоль линии ее действия?
5. В каком случае момент силы относительно данной точки равен нулю?
6. Какая система сил называется парой сил, чему равен момент пары сил?
7. Что называют связью? В чем заключается принцип освобождения от связей? Перечислите основные типы связей, покажите их реакции.
8. Каковы условия и уравнения равновесия системы сходящихся и произвольной систем сил, расположенных в пространстве и в плоскости?
9. Сформулируйте порядок решения задач статики.
2. Кинематика
Кинематика- раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела. Соответственно, изучение делят на кинематику точки и кинематику твердого тел
2.1 Основные понятия кинематики
Закон движения точки (тела) – зависимость положения точки (тела) в пространстве от времени.
Траектория точки – геометрическое место положений точки в пространстве при ее движении.
Скорость точки (тела) – характеристика изменения во времени положения точки (тела) в пространстве.
Ускорение точки (тела) – характеристика изменения во времени скорости точки (тела)
Похожие работы
... , а в ходе решения обрести уверенность, что ответ получен правильный. Для этого решение необходимо проверить, специалисты сказали бы – «провести экспертизу проекта». В пособии показано, как в задачах статики можно провести подобную экспертизу, то есть путем проверки убедиться в правильности решения. Общие методические указания Основная практическая задача статики - определение реакций связей, ...
... : Составить кинетические соотношения: Вычислим кинетическую энергию системы в конечном положении: Найдем сумму работ всех внешних сил на заданном перемещении: Для определения скорости воспользуемся уравнением: Ответ: 4. D19. Применение общего управления динамики к исследованию движения механической системы с одной степенью свободы Дано: ...
... Сербо «Сборник задач по теоретической механике», - М.: «Наука», 1977 г., - 320 с. И.В. Мещерский «Сборник задач по теоретической механике», - М.: «Наука», 1986 г., - 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», - М.: «Высшая школа» 1984 г., - 319 с. Студент-практикант: Филатов А.С.7 “Согласовано” “Утверждено” Преподаватель Джежеря ...
... условий взаимной уравновешенности системы сил является одной из основных задач статики. На основе изложенной в первой главе курсовой работы алгоритм конструкции языка программирования Паскаль составим и решим ряд задач по прикладной механике. Сформулируем задачу по статике первому разделу прикладной механики. Задача. Найти центр тяжести тонкого круглого однородного стержня изогнутого по дуге ...
0 комментариев