Навигация
2.3. Кинематика твердого тела
В отличие от кинематики точки в кинематике твердых тел решаются две основные задачи:
- задание движения и определение кинематических характеристик тела в целом;
- определение кинематических характеристик точек тела.
Способы задания и определения кинематических характеристик зависят от типов движения тел.
В настоящем пособии рассматриваются три типа движения: поступательное, вращательное вокруг неподвижной оси и плоско-параллельное движение твердого тела
2.3.1. Поступательное движение твердого тела
Поступательным называют движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению (рис.2.8).
Доказана теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения (рис.2.8).
Вывод: Поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
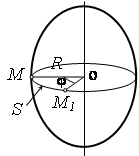
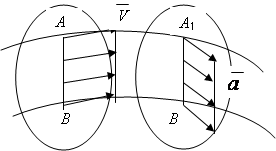
Рис. 2.8 Рис. 2.9
2.3.2 Вращательное движение твердого тела вокруг неподвижной оси.
Вращательным вокруг неподвижной оси называют движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
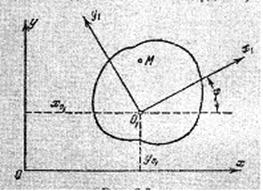
Положение тела определяется углом поворота j (рис.2.9 ). Единица измерения угла – радиан. (Радиан - центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2p радиана.)
Закон вращательного движения тела вокруг неподвижной оси j = j(t). Угловую скорость и угловое ускорение тела определим методом дифференцирования
![]() - угловая скорость, рад/с; (2.10)
- угловая скорость, рад/с; (2.10)
 - угловое ускорение, рад/с2 (2.11)
- угловое ускорение, рад/с2 (2.11)
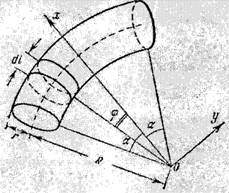
При вращательном движении тела вокруг неподвижной оси его точки, не лежащие на оси вращения, движутся по окружностям с центром на оси вращения.
Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точка М, то точка М будет описывать вокруг точки С окружность радиуса R (рис. 2.9). За время dt происходит элементарный поворот на угол ![]() , при этом точка М совершит перемещение вдоль траектории на расстояние
, при этом точка М совершит перемещение вдоль траектории на расстояние ![]() .Определим модуль линейной скорости:
.Определим модуль линейной скорости:
 ( 2.12 )
( 2.12 )
Ускорение точки М при известной траектории определяется по его составляющим, см.(2.8)
![]() ,
,
где: ![]() ;
; 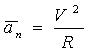 .
.
Подставляя в формулы выражение (2.12) получим:
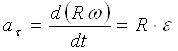 , .
, .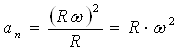 , (2.13)
, (2.13)
где: ![]() - тангенциальное ускорение,
- тангенциальное ускорение,
![]() -нормальное ускорение.
-нормальное ускорение.
2.3.3. Плоско - параллельное движение твердого тела
Плоскопараллельным называется движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости (рис.2.10). Для изучения движения тела достаточно изучить движение одного сечения S этого тела плоскостью, параллельной неподвижной плоскости. Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений: а) поступательного и вращательного; б) вращательного относительно подвижного (мгновенного) центра.
В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса (рис.2.11). В качестве полюса может быть принята любая точка сечения.
 | |||
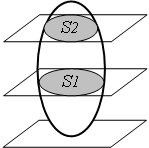 | |||
Рис. 2.10 Рис. 2.11
Уравнения движения запишутся в виде:
![]() ХА = ХА (t)
ХА = ХА (t)
YА = YА (t) ( 2.14 )
jА = jА (t)
Кинематические характеристики полюса определяют из уравнений его движения.
Скорость любой точки плоской фигуры, движущейся в своей плоскости слагается из скорости полюса (произвольно выбранной в сечении точки А) и скорости вращательного движения вокруг полюса (вращение точки В вокруг точки А).
Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса.
![]()
![]() (2.15 )
(2.15 )
![]() (2.16 )
(2.16 )
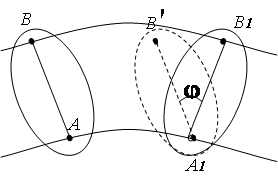
Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P (рис.1.12). В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения
![]() (2.17 )
(2.17 )
Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.
 (2.18)
(2.18)
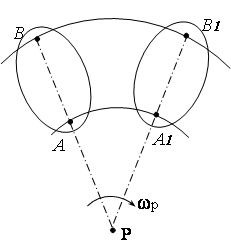
Рис.2.12
Положение мгновенного центра вращения может быть определено на основании следующих свойств:
- вектор скорости точки перпендикулярен радиусу;
- модуль скорости точки пропорционален расстоянию от точки до центра вращения ( V= w ∙R) ;
- скорость в центре вращения равна нулю.
Рассмотрим некоторые случаи определения положения мгновенного центра.
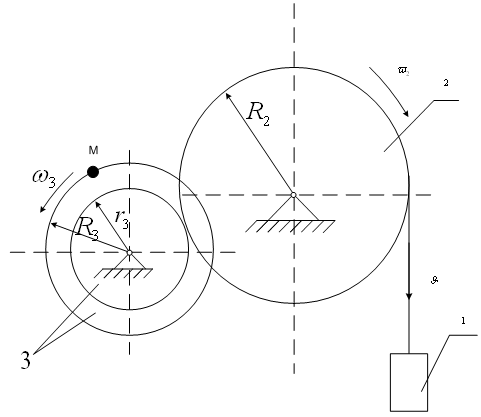
1. Известны направления скоростей двух точек плоской фигуры (рис.2.13). Проведем линии радиусов. Мгновенный центр вращения Р находится на пересечении перпендикуляров, проведенных к векторам скоростей.
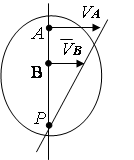
2. Скорости точек А и В известны, причем вектора ![]() и
и ![]() параллельны друг другу, а линия АВ перпендикулярна
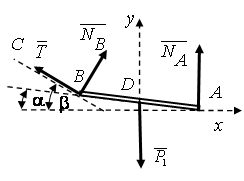
параллельны друг другу, а линия АВ перпендикулярна ![]() (рис. 2. 14). В этом случае мгновенный центр вращения лежит на линии АВ. Для его нахождения проведем линию пропорциональности скоростей на основании зависимости V= wR.
(рис. 2. 14). В этом случае мгновенный центр вращения лежит на линии АВ. Для его нахождения проведем линию пропорциональности скоростей на основании зависимости V= wR.
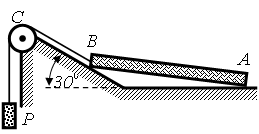
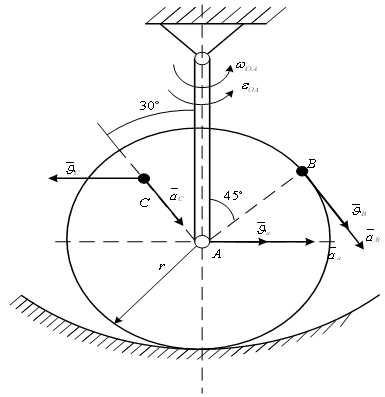
3. Тело катится без скольжения по неподвижной поверхности другого тела (рис.2.15). Точка касания тел в данный момент имеет нулевую скорость в то время, как скорости других точек тела не равны нулю. Точка касания Р будет мгновенным центром вращения.
 | |||||
 | |||||
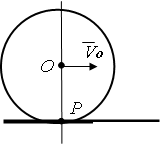 | |||||
Рис. 2.13 Рис. 2.14 Рис. 2.15
Кроме рассмотренных вариантов скорость точки сечения может быть определена на основании теоремы о проекциях скоростей двух точек твердого тела.
Теорема: проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены.
Доказательство: расстояние АВ изменяться не может, следовательно,
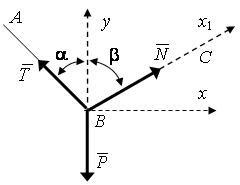
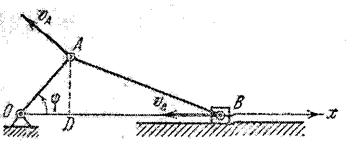
VА cosa не может быть больше или меньше VВ cosb (рис.2.16 ).
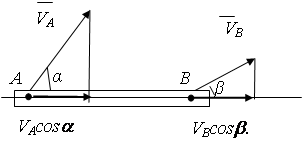 | |||
Рис. 2.16
Вывод: VАcosa =VВcosb. (2.19 )
Похожие работы
... , а в ходе решения обрести уверенность, что ответ получен правильный. Для этого решение необходимо проверить, специалисты сказали бы – «провести экспертизу проекта». В пособии показано, как в задачах статики можно провести подобную экспертизу, то есть путем проверки убедиться в правильности решения. Общие методические указания Основная практическая задача статики - определение реакций связей, ...
... : Составить кинетические соотношения: Вычислим кинетическую энергию системы в конечном положении: Найдем сумму работ всех внешних сил на заданном перемещении: Для определения скорости воспользуемся уравнением: Ответ: 4. D19. Применение общего управления динамики к исследованию движения механической системы с одной степенью свободы Дано: ...
... Сербо «Сборник задач по теоретической механике», - М.: «Наука», 1977 г., - 320 с. И.В. Мещерский «Сборник задач по теоретической механике», - М.: «Наука», 1986 г., - 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», - М.: «Высшая школа» 1984 г., - 319 с. Студент-практикант: Филатов А.С.7 “Согласовано” “Утверждено” Преподаватель Джежеря ...
... условий взаимной уравновешенности системы сил является одной из основных задач статики. На основе изложенной в первой главе курсовой работы алгоритм конструкции языка программирования Паскаль составим и решим ряд задач по прикладной механике. Сформулируем задачу по статике первому разделу прикладной механики. Задача. Найти центр тяжести тонкого круглого однородного стержня изогнутого по дуге ...




0 комментариев