Навигация
2.4. Сложное движение точки
В предыдущих параграфах рассматривалось движение точки относительно неподвижной системы отсчета, так называемое абсолютное движение. В практике встречаются задачи, в которых известно движение точки относительно системы координат, которая движется относительно неподвижной системы. При этом требуется определить кинематические характеристики точки относительно неподвижной системы.
Принято называть: движение точки относительно подвижной системы – относительным, движение точки вместе с подвижной системой – переносным, движение точки относительно неподвижной системы – абсолютным. Соответственно называют скорости и ускорения:
-относительные;
- переносные; 
-абсолютные.
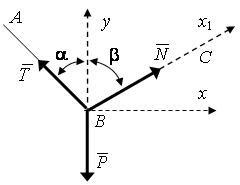
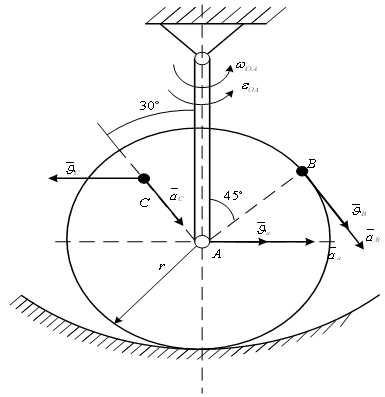
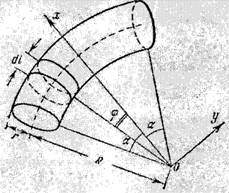
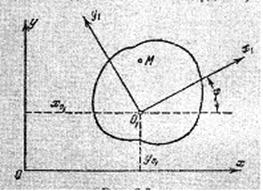
Согласно теореме о сложении скоростей абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (рис.).
, (2.20)
Абсолютное значение скорости определяется по теореме косинусов
, (2.21)
Рис.2.17
Ускорение по правилу параллелограмма определяется только при поступательном переносном движении
, (2.22)
При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым.
, (2.23)
где 
Кориолисово ускорение численно равно
,
где a – угол между векторами 
и 
Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор 
спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.
2.5 Вопросы для самоконтроля по разделу
1. В чем состоят основные задачи кинематики? Назовите кинематические характеристики.
2. Назовите способы задания движения точки и определение кинематических характеристик.
3. Дайте определение поступательного, вращательного вокруг неподвижной оси, плоскопараллельного движения тела.
4. Как задается движение твердого тела при поступательном, вращательном вокруг неподвижной оси и плоскопараллельном движении тела и как определяется скорость и ускорение точки при этих движениях тела?
3. Динамика
3.1 Задачи динамики
В динамике решаются два типа задач. Первая состоит в определении действующих сил при заданном законе движения материального объекта (точки или системы). Вторая задача обратная первой: определяется закон движения материального объекта при известных действующих на него силах.
3.2. Основные понятия динамики
Инерционность - свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.
Масса - количественная мера инерционности тела. Единица измерения массы - килограмм (кг).
Материальная точка - тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.
Центр масс механической системы - геометрическая точка, координаты которой определяются формулами.
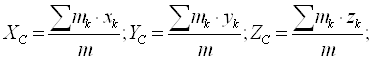(3.1 )
где mk, xk, yk, zk- масса и координаты k - той точки механической системы,
m - масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.
Момент инерции материального тела относительно оси – количественная мера инертности при вращательном движении.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси.
JZ = m×r2 (3.2)
Момент инерции системы (тела ) относительно оси равен арифметической сумме моментов инерции всех точек.
JZ = åmk×rk2 (3.3 )
Сила инерции материальной точки - векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения
(3.4)
Сила инерции материального тела - векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс
, (3.5)
где 
- ускорение центра масс тела.
Элементарный импульс силы - векторная величина 
, равная произведению вектора силы 
на бесконечно малый промежуток времени dt
, (3.6)
Полный импульс силы за Dt равен интегралу от элементарных импульсов
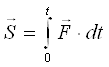(3.7)
Элементарная работа силы - скалярная величина dA, равная скалярному произведению вектора силы 
на бесконечно малое перемещение d
.
Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов.
dA = F×ds×cosa, (3.8)
где a - угол между направлениями векторов перемещения и силы.
Работа силы 
на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению.
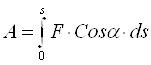(3.9)
Единица измерения работы - Джоуль (1 Дж=1 Н×м).
Количество движения материальной точки - векторная величина 
, равная произведению массы m на её скорость 
.
= 
(3.10)
Количество движения механической системы 
равно векторной сумме количества движения её точек.
(3.11)
или с учетом формул ( 3.1 ).
, (3.12)
где: m- масса механической системы,
- вектор скорости центра масс системы.
Кинетическая энергия материальной точки - скалярная величина Т, равная половине произведения массы точки на квадрат её скорости.
T=
(3.13)
Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек.
(3.14)
Похожие работы
... , а в ходе решения обрести уверенность, что ответ получен правильный. Для этого решение необходимо проверить, специалисты сказали бы – «провести экспертизу проекта». В пособии показано, как в задачах статики можно провести подобную экспертизу, то есть путем проверки убедиться в правильности решения. Общие методические указания Основная практическая задача статики - определение реакций связей, ...
... : Составить кинетические соотношения: Вычислим кинетическую энергию системы в конечном положении: Найдем сумму работ всех внешних сил на заданном перемещении: Для определения скорости воспользуемся уравнением: Ответ: 4. D19. Применение общего управления динамики к исследованию движения механической системы с одной степенью свободы Дано: ...
... Сербо «Сборник задач по теоретической механике», - М.: «Наука», 1977 г., - 320 с. И.В. Мещерский «Сборник задач по теоретической механике», - М.: «Наука», 1986 г., - 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», - М.: «Высшая школа» 1984 г., - 319 с. Студент-практикант: Филатов А.С.7 “Согласовано” “Утверждено” Преподаватель Джежеря ...
... условий взаимной уравновешенности системы сил является одной из основных задач статики. На основе изложенной в первой главе курсовой работы алгоритм конструкции языка программирования Паскаль составим и решим ряд задач по прикладной механике. Сформулируем задачу по статике первому разделу прикладной механики. Задача. Найти центр тяжести тонкого круглого однородного стержня изогнутого по дуге ...
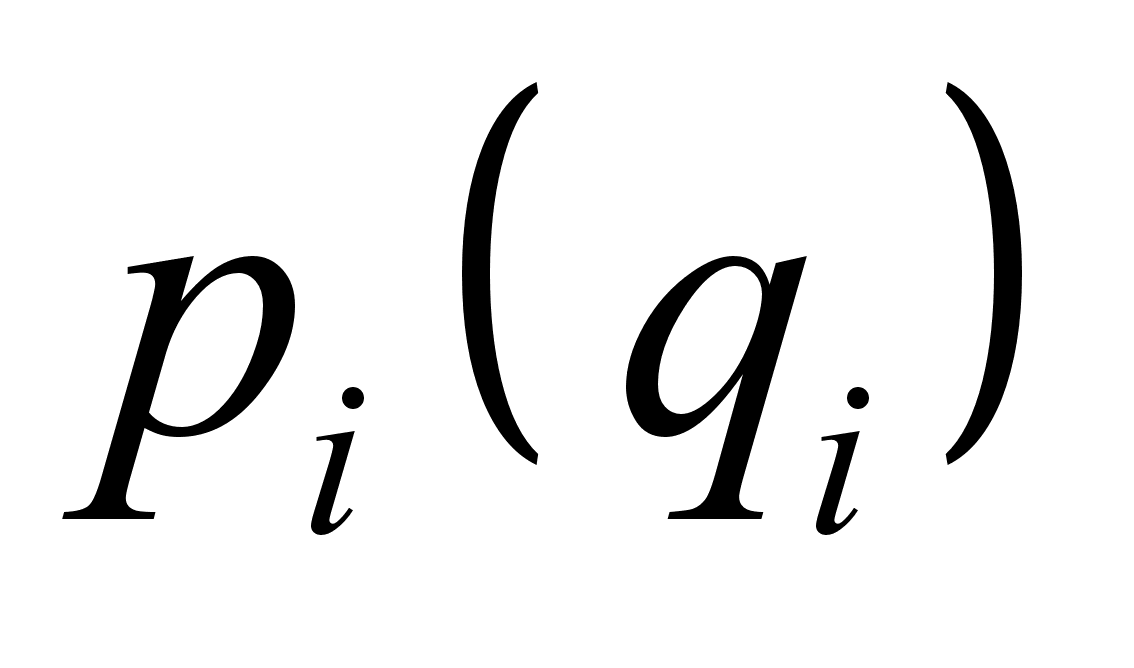
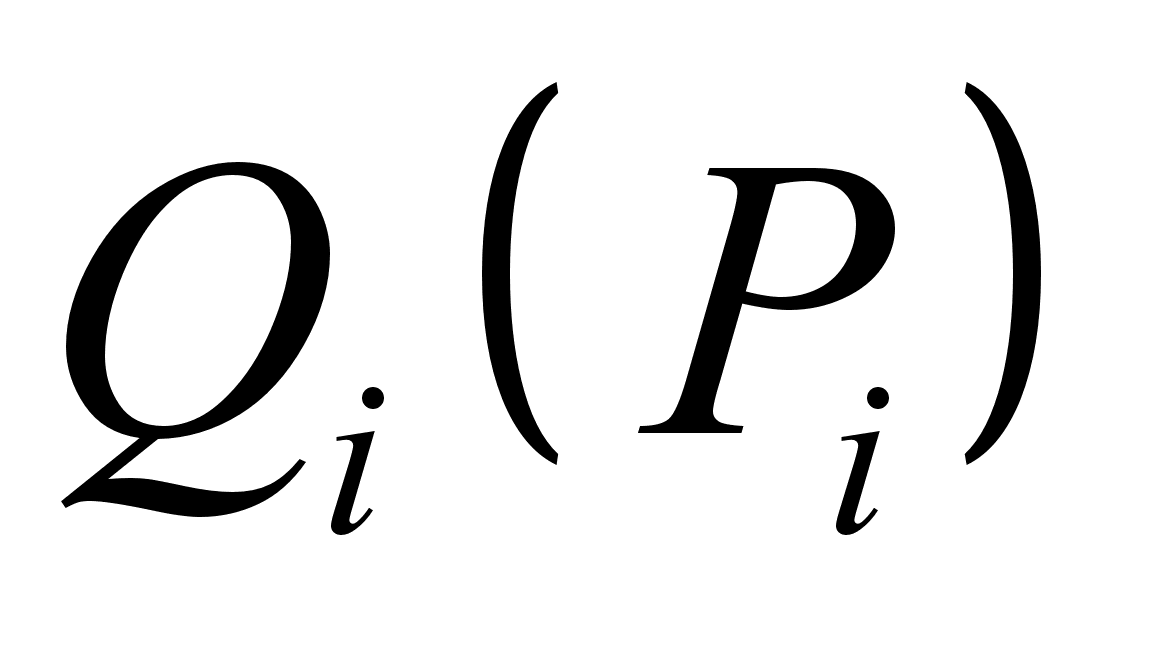
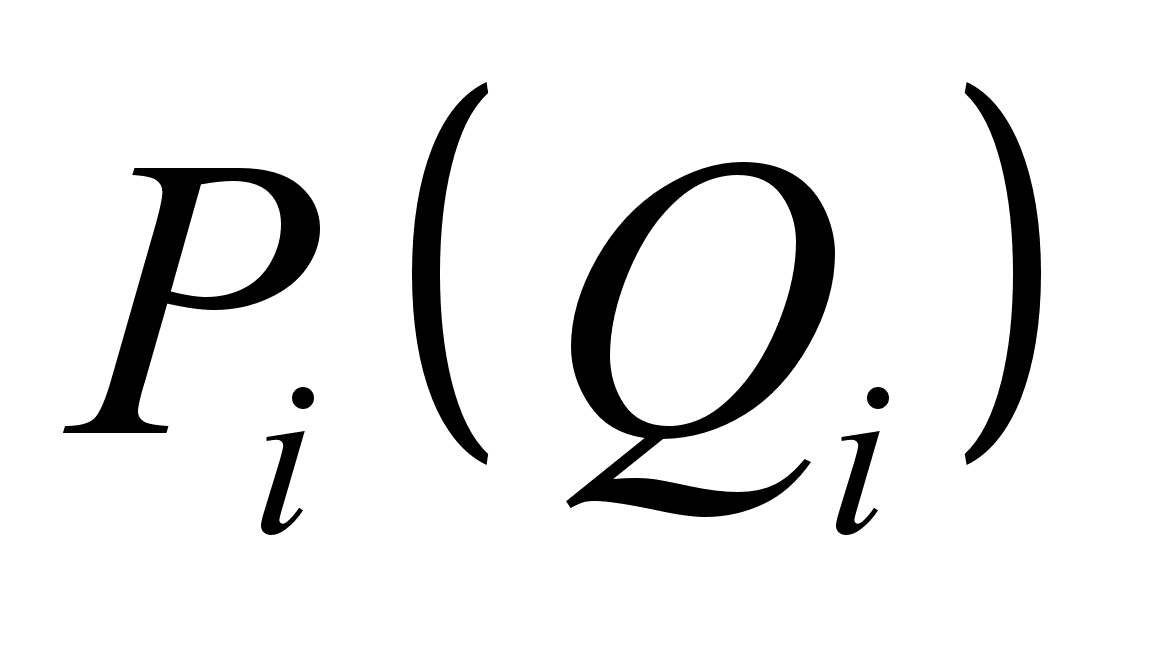
0 комментариев