Навигация
Обертання площини поляризації
4. Обертання площини поляризації
При проходженні лінійно-поляризованого світла через оптично активні речовини (кварц, розчин цукру) площина поляризації світла обертається навколо напрямку поширення променя. Кут повороту ![]() пропорційний шляху
пропорційний шляху ![]() , пройденому променем в речовині:
, пройденому променем в речовині:
![]() (5.43)
(5.43)
Коефіцієнт ![]() називають постійною обертання.
називають постійною обертання.
В розчинах кут повороту площини поляризації пропорційний шляху променя в розчині ![]() і концентрації розчину С:
і концентрації розчину С:
![]() (5.44)
(5.44)
де ![]() – питома постійна обертання.
– питома постійна обертання.
Залежність (5.44) використовується для вимірювання невідомої концентрації ![]() за відомою концентрацією розчину
за відомою концентрацією розчину ![]()
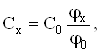 (5.45)
(5.45)
де ![]() – кут повороту для невідомої концентрації,
– кут повороту для невідомої концентрації, ![]() – кут повороту для відомої концентрації.
– кут повороту для відомої концентрації.
Явище оптичної активності покладене в основу роботи цукрометрів – приладів для вимірювання концентрації розчинів.
§ 5.6. Квантова природа випромінювання. Теплове випромінювання
Нагріті тіла випромінюють електромагнітні хвилі. Це відбувається внаслідок перетворення енергії теплового руху молекул тіла в енергію випромінювання. Теплове випромінювання знаходиться в рівновазі з випромінюючим тілом, тобто розподіл енергії між тілом і випромінюванням лишається незмінним для кожної довжини хвилі. Таке випромінювання називається рівноважним.
Розглянемо закони теплового випромінювання. Введемо випромінювальну здатність ![]() – кількість енергії, яка випромінюється одиницею площі поверхні тіла за одиницю часу в одиничному інтервалі частот. Енергетична світність, або інтегральна випромінювальна здатність
– кількість енергії, яка випромінюється одиницею площі поверхні тіла за одиницю часу в одиничному інтервалі частот. Енергетична світність, або інтегральна випромінювальна здатність ![]() – це кількість енергії, яка випромінюється одиницею площі за одиницю часу у всьому спектральному діапазоні, тобто
– це кількість енергії, яка випромінюється одиницею площі за одиницю часу у всьому спектральному діапазоні, тобто
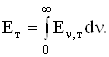 (5.46)
(5.46)
Поглинальна здатність ![]() визначає долю енергії
визначає долю енергії ![]() падаючих електромагнітних хвиль за одиницю часу на одиницю площі поверхні тіла в діапазоні частот від
падаючих електромагнітних хвиль за одиницю часу на одиницю площі поверхні тіла в діапазоні частот від ![]() до
до ![]() яка поглинається тілом:
яка поглинається тілом:
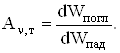 (5.47)
(5.47)
Тіло називається абсолютно чорним, якщо воно при будь-якій температурі повністю поглинає всі падаючі на нього електромагнітні хвилі:
![]() . (5.48)
. (5.48)
Для довільної частоти і температури відношення випромінювальної здатності тіла до його поглинальної здатності однакове для всіх тіл і дорівнює випромінювальній здатності ![]() абсолютно чорного тіла:
абсолютно чорного тіла:
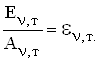 . (5.49)
. (5.49)
Це є закон Кірхгофа в диференціальній формі.
Інтегральна випромінювальна здатність ![]() абсолютно чорного тіла:
абсолютно чорного тіла:
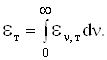 (5.50)
(5.50)
Планк у 1900р. на основі квантових уявлень про випромінювання отримав аналітичний вираз ![]() Згідно Планку енергія кванта випромінювання пропорційна частоті:
Згідно Планку енергія кванта випромінювання пропорційна частоті:
![]() (5.51)
(5.51)
де ![]() – стала Планка.
– стала Планка.
В результаті,
![]()
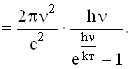 (5.52)
(5.52)
На мал.5.21 зображена залежність спектральної випромінювальної здат-ності абсолютно чорного тіла для різних температур. Площа під кривою ![]() визначає інтегральну випромінювальну здатність абсолютно чорного тіла.
визначає інтегральну випромінювальну здатність абсолютно чорного тіла.
Підставляючи (5.52) в (5.50) і інтегруючи, знайдемо
![]() (5.53)
(5.53)
Отже, інтегральна випромінювальна здатність абсолютно чорного тіла пропорційна четвертій степені абсолютної температури. Це є закон Стефана-Больцмана. У формулі (5.53) ![]() – постійна Стефана-Больцмана.
– постійна Стефана-Больцмана.
Досліджуючи вираз спектральної випромінювальної здатності на екстремум, знайдемо, що частота ![]() при якій спостерігається максимум спектральної випромінювальної здатності абсолютно чорного тіла, пропорційна температурі, або відповідна довжина хвилі
при якій спостерігається максимум спектральної випромінювальної здатності абсолютно чорного тіла, пропорційна температурі, або відповідна довжина хвилі
![]() (5.54)
(5.54)
Це – закон зміщення Віна. Стала ![]() . Згідно закону Віна, максимум спектральної випромінювальної здатності при зростанні температури тіла зміщується у високочастотну ділянку спектра.
. Згідно закону Віна, максимум спектральної випромінювальної здатності при зростанні температури тіла зміщується у високочастотну ділянку спектра.
На законах Стефана-Больцмана і Віна базується робота пірометрів – приладів, які дозволяють вимірювати високі температури.
§ 5.7. Фотоефект
Розрізняють зовнішній і внутрішній фотоефект. Внутрішній фотоефект спостерігається в напівпровідниках і полягає в тому, що під дією світла електрони відриваються від атома, але залишаються всередині кристалу, в результаті чого збільшується провідність напівпровідника.
Зовнішній фотоефект – це явище виривання електронів з поверхні металу під дією світла. Зовнішній фотоефект був відкритий Герцем у 1887 р. і досліджений Столєтовим у 1888-89 рр. Схема дослідів Столєтова приведена на мал 5.22.
Основні закономірності фотоефекту:
1. сила фотоструму прямо пропор-ційна інтенсивності світла, яке падає на катод;
2. фотоефект – безінерційний;
3. кінетична енергія вирваних елек-тронів збільшується зі збільшенням частоти падаючого світла. Існує мінімальна частота, з якої починається фотоефект. Це – червона межа фотоефекту.
Теоретичне пояснення фото-ефекту дав Ейнштейн у 1905 р. Він використав гіпотезу Планка про квантову природу випромінювання світла і припустив, що енергія поглинутого кванта йде на роботу виходу електрона з металу і на надання електрону кінетичної енергії:
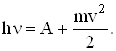 (5.55)
(5.55)
Це – рівняння Ейнштейна для фотоефекту. З рівняння (5.55) можна знайти найменшу частоту ![]() при якій починається фотоефект. Це і є червона межа фотоефекту:
при якій починається фотоефект. Це і є червона межа фотоефекту:
![]() (5.56)
(5.56)
§ 5.8. Тиск світла
Тиск світла можна пояснити з квантової точки зору. Кванти світла (фотони) мають масу та імпульс. Маса фотона ![]() визначається з релятивістського співвідношення Ейнштейна
визначається з релятивістського співвідношення Ейнштейна ![]() Звідки, враховуючи (5.51), отримаємо
Звідки, враховуючи (5.51), отримаємо
![]() (5.57)
(5.57)
Залежність маси від швидкості ![]() в застосуванні до фотона
в застосуванні до фотона ![]() має зміст лише при
має зміст лише при ![]() Це означає, що маса спокою фотона рівна нулю.
Це означає, що маса спокою фотона рівна нулю.
Імпульс фотона, з врахуванням (5.57),
![]() (5.58)
(5.58)
Нехай на одиницю поверхні тіла за одиницю часу падає n фотонів. При цьому ![]() – число відбитих фотонів (R – коефіцієнт відбивання), і (1-R)n – число поглинутих фотонів. Тоді, за другим законом Ньютона, зміна імпульсу площадки визначатиме тиск світла:
– число відбитих фотонів (R – коефіцієнт відбивання), і (1-R)n – число поглинутих фотонів. Тоді, за другим законом Ньютона, зміна імпульсу площадки визначатиме тиск світла:
![]() (5.59)
(5.59)
Враховуючи, що ![]() – інтенсивність світла, отримаємо:
– інтенсивність світла, отримаємо:
![]() . (5.60)
. (5.60)
Для дзеркальної поверхні ![]()
![]() , а для чорної (
, а для чорної (![]()
![]() . Таким чином, тиск на дзеркальну поверхню – вдвічі більший, ніж на чорну, що і спостерігав П.М.Лєбєдєв в своїх дослідах з вимірювання тиску світла.
. Таким чином, тиск на дзеркальну поверхню – вдвічі більший, ніж на чорну, що і спостерігав П.М.Лєбєдєв в своїх дослідах з вимірювання тиску світла.
§ 5.9. Ефект Комптона
Досліджуючи розсіювання рентгенівських променів в кристалах, Комптон (1923 р.) встановив, що в розсіяному випромінюванні, крім незміщеної компоненти з довжиною хвилі ![]() , існує зміщена компонента з довжиною хвилі
, існує зміщена компонента з довжиною хвилі ![]() . При розсіюванні легкими атомами (
. При розсіюванні легкими атомами (![]()
![]() В) практично все розсіяне випромінювання має зміщену довжину хвилі. По мірі збільшення атомного номера все більша частина випромінювання розсіюється без зміни довжини хвилі.
В) практично все розсіяне випромінювання має зміщену довжину хвилі. По мірі збільшення атомного номера все більша частина випромінювання розсіюється без зміни довжини хвилі.
Ефект Комптона можна пояснити з квантової точки зору, як процес непружного розсіювання рентгенівських фотонів на вільних електронах. Вільними можна вважати слабо зв’язані з атомами електрони.
Нехай ![]() і
і ![]() – значення енергії і імпульсу фотона до розсіювання. Після зіткнення енергія і імпульс фотона зменшуються:
– значення енергії і імпульсу фотона до розсіювання. Після зіткнення енергія і імпульс фотона зменшуються: ![]() і
і ![]() . Звідси випливає, що
. Звідси випливає, що ![]() . Тобто, в результаті розсіювання частота фотона зменшується (довжина хвилі збільшується). Згідно законів збереження енергії і імпульсу, зміна довжини хвилі фотона при розсіюванні
. Тобто, в результаті розсіювання частота фотона зменшується (довжина хвилі збільшується). Згідно законів збереження енергії і імпульсу, зміна довжини хвилі фотона при розсіюванні
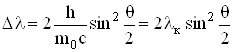 , (5.61)
, (5.61)
де  – стала величина, яка називається комптонівською довжиною хвилі тієї вільної частинки, на якій відбувається розсіювання (
– стала величина, яка називається комптонівською довжиною хвилі тієї вільної частинки, на якій відбувається розсіювання (![]() – маса спокою вільної частинки).
– маса спокою вільної частинки).
Для електрона ![]() .
.
Формула (5.61) добре узгоджується з результатами експериментальних досліджень ефекту Комптона.
Таким чином, світло одночасно має властивості неперервних електромагнітних хвиль (інтерференція, дифракція) і властивості дискретних фотонів (фотоефект, ефект Комптона). Воно являє собою діалектичну єдність цих протилежних властивостей. В прояві хвильових і корпускулярних властивостей світла є закономірність: при зменшенні довжини хвилі більш чітко проявляються квантові властивості і навпаки, у довгохвильового випромінювання основну роль відіграють його хвильові характеристики.
Можна зробити висновок, що корпускулярні і хвильові властивості світла не виключають, а, навпаки, взаємно доповнюють одна одну. Зв’язок між корпускулярними і хвильовими характеристиками світла виражається формулою
![]() , (5.62)
, (5.62)
де ![]() – довжина хвилі, p – імпульс фотона, h – стала Планка.
– довжина хвилі, p – імпульс фотона, h – стала Планка.
Квадрат амплітуди світлової хвилі в деякій точці простору являється мірою імовірності попадання фотонів в цю точку. Корпускулярні властивості зумовлені тим, що енергія, імпульс і маса випромінювання локалізовані в дискретних частинках – фотонах, хвильові – статистичними закономірностями розподілу фотонів у просторі.
§ 5.10. Гальмівне рентгенівське випромінювання
Рентгенівські промені (![]() виникають при бомбардуванні швидкими електронами твердих тіл. Такий процес реалізується в рентгені-вських трубках. У найпростішому випадку це – двоелектродна ва-куумна трубка (мал.5. 23), катод К якої є джерелом електронів, що виникають внаслідок явища термоелектронної емісії. Анод А, виготовлений із важких металів (Cu, Fe, Co, W тощо), служить мішенню.
виникають при бомбардуванні швидкими електронами твердих тіл. Такий процес реалізується в рентгені-вських трубках. У найпростішому випадку це – двоелектродна ва-куумна трубка (мал.5. 23), катод К якої є джерелом електронів, що виникають внаслідок явища термоелектронної емісії. Анод А, виготовлений із важких металів (Cu, Fe, Co, W тощо), служить мішенню.
Якщо між катодом і анодом прикладена велика напруга U, то електрони розганяються до енергій еU=104–105еВ. Попадаючи в речовину анода, електрони сильно гальмуються і тому випромінюють електромагнітні хвилі – гальмівне рентгенівське випромінювання.
Відомо, що заряд, який рухається прискорено, є джерелом електромагнітних хвиль із неперервним спектром. Спектр гальмівного рентгенівського випромі-нювання (мал.5.24) хоч і суцільний, але обмежений з боку малих довжин хвиль так званою короткохвильовою межею ![]() . З ростом прискорюючої напруги U
. З ростом прискорюючої напруги U ![]() зменшується. Класична електродинаміка не пояснює появи короткохвильової межі гальмівного випромінювання. Її існування безпосередньо випливає з квантової природи випромінювання. Якщо врахувати, що максимальна енергія рентгенівського кванта не може перевищувати кінетичної енергії електрона, то
зменшується. Класична електродинаміка не пояснює появи короткохвильової межі гальмівного випромінювання. Її існування безпосередньо випливає з квантової природи випромінювання. Якщо врахувати, що максимальна енергія рентгенівського кванта не може перевищувати кінетичної енергії електрона, то
![]() . (5.63)
. (5.63)
Звідси
![]() , (5.64)
, (5.64)
що відповідає експериментальним вимірюванням. Оскільки електрон віддає довільну частину своєї енергії, то поява електромагнітного випромінювання різних довжин хвиль цілком зрозуміла.
При достатньо великій швидкості електронів, крім гальмівного випромінювання, виникає також характеристичне випромінювання. Воно зумовлене збудженням внутрішніх електронних оболонок атомів. Рентгенівський спектр характеристичного випромінювання – дискретний.
§ 5.11. Елементи теорії відносності (релятивістська механіка)
Рух тіл зі швидкостями значно меншими від швидкості світла у вакуумі (![]() описується законами класичної механіки.
описується законами класичної механіки.
Розглянемо будь-які дві інерціальні системи відліку К і ![]() (мал.5.25). Перетворення координат Галілея для переходу від однієї інерціальної системи відліку
(мал.5.25). Перетворення координат Галілея для переходу від однієї інерціальної системи відліку ![]() до іншої К(х,у,z) у випадку, показаному на мал.5.25, мають вигляд:
до іншої К(х,у,z) у випадку, показаному на мал.5.25, мають вигляд:
 (5.65)
(5.65)
де v0 – швидкість руху системи ![]() відносно К (при t=0 початки координат систем відліку співпадають). З перетворень координат Галілея випливає правило додавання швидкостей
відносно К (при t=0 початки координат систем відліку співпадають). З перетворень координат Галілея випливає правило додавання швидкостей ![]() (5.66)
(5.66)
де ![]() – швидкість тіла у системі К,
– швидкість тіла у системі К, ![]() – його швидкість у системі відліку
– його швидкість у системі відліку ![]()
Величини відрізків і проміжки часу при переході від однієї системи відліку до іншої не змінюються:
![]() (5.67)
(5.67)
В класичній механіці простір і час розглядаються незалежно один від одного. Механічні закони незмінні (інваріантні) при переході від однієї системи відліку до іншої. Інваріантність законів механіки відносно перетворень координат Галілея є математичним виразом механічного принципу відносності: у різних інерціальних системах відліку всі механічні процеси при рівних умовах протікають однаково, тобто всі інерціальні системи відліку рівноправні між собою.
Якщо швидкість тіл наближається до швидкості світла у вакуумі, то закони класичної механіки перестають бути справедливими. У цьому випадку слід користуватись спеціальною теорією відносності – релятивістською механікою.
Спеціальна теорія відносності грунтується на двох постулатах Ейнштейна. Перший постулат: всі закони природи інваріантні при переході від однієї інерціальної системи відліку до іншої. Ейнштейн, фактично, поширив механічний принцип відносності Галілея на всі фізичні явища. Другий постулат: швидкість світла у вакуумі однакова у всіх інерціальних системах відліку і не залежить від руху джерел і приймачів світла.
Ці два принципи являють собою основу спеціальної теорії відносності, яка, в свою чергу, є теорією простору і часу.
В спеціальній теорії відносності замість перетворень Галілея слід користуватись перетвореннями Лоренца. У простому випадку, коли координатні осі 0Х і ![]() співпадають, перетворення координат Лоренца мають вигляд:
співпадають, перетворення координат Лоренца мають вигляд:
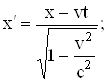
![]()
![]()
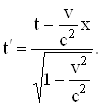 (5.68)
(5.68)
Зауважимо, що перетворення Лоренца при v<<c переходять у перетворення Галілея.
З перетворень Лоренца випливають два важливих наслідки. По-перше, довжина тіла l, виміряна в системі (К), відносно якої воно рухається, виявляється меншою довжини тіла l0, виміряної в системі (![]() ), відносно якої тіло нерухоме
), відносно якої тіло нерухоме
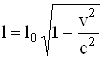 . (5.69)
. (5.69)
Систему відліку (![]() , відносно якої тіло нерухоме, називають власною системою відліку.
, відносно якої тіло нерухоме, називають власною системою відліку.
По-друге, власний проміжок часу ![]() менший проміжку часу
менший проміжку часу ![]() , відрахованого за годинником, який рухається відносно тіла
, відрахованого за годинником, який рухається відносно тіла
 . (5.70)
. (5.70)
Власний час ![]() відраховується за годинником системи відліку, яка рухається разом з тілом.
відраховується за годинником системи відліку, яка рухається разом з тілом.
Залежність маси m від швидкості його руху дається рівнянням:
m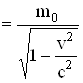 , (5.71)
, (5.71)
де m0 – маса спокою тіла.
Динаміка руху тіла в релятивістській механіці описується рівнянням
![]() , (5.72)
, (5.72)
де 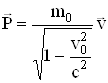 (5.73)
(5.73)
є релятивістський імпульс.
Між повною енергією тіла і його релятивістською масою існує взаємозв’язок,
W=mc2. (5.74)
Цю залежність називають законом взаємозв’язку маси і енергії.
Енергію W0=m0c2 (5.75)
називають енергією спокою тіла.
Кінетична енергія тіла
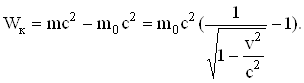 (5.76)
(5.76)
У випадку малих швидкостей ця формула переходить у відомий вираз
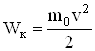 . (5.77)
. (5.77)
Зв’язок між повною енергією та імпульсом
![]() . (5.78)
. (5.78)
Головний висновок теорії відносності: простір і час органічно взаємно пов’язані і утворюють єдину форму існування матерії – простір-час. Саме тому просторово-часовий інтервал між двома подіями – абсолютний (однаковий у всіх інерціальних системах):
![]()
![]() (5.79)
(5.79)
Окремо взяті просторові і часові проміжки між подіями – відносні.
Таким чином, перетворення Лоренца і всі висновки, які з них випливають, визначають об’єктивно існуючі просторово-часові співвідношення рухомої матерії.
Розділ VI. Елементи атомної фізики, квантової механіки і фізики твердого тіла.
§ 6. 1. Ядерна модель атома. Воднеподібний атом Бора. Спектральні серії
Оскільки світло випромінюється і поглинається атомами речовини, то виникає питання: яка структура атомів забезпечує квантовий (дискретний) характер вказаних процесів? Відповідь на це питання дав Резерфорд (1911р), аналізуючи результати експериментального дослідження розсіяння ![]() -частинок на тонких металічних плівках. Він запропонував ядерну модель атома, згідно з якою в центрі атома
-частинок на тонких металічних плівках. Він запропонував ядерну модель атома, згідно з якою в центрі атома ![]() розміщене позитивно заряджене ядро
розміщене позитивно заряджене ядро ![]() , в якому сконцентрована практично вся маса атома. Навколо ядер по колових чи еліптичних орбітах рухаються електрони. Якщо в нейтральному атомі Z електронів, то заряд ядра
, в якому сконцентрована практично вся маса атома. Навколо ядер по колових чи еліптичних орбітах рухаються електрони. Якщо в нейтральному атомі Z електронів, то заряд ядра ![]() , де
, де ![]() – елементарний заряд.
– елементарний заряд.
Рух електрона по орбіті є прискореним. І тому, з точки зору класичної фізики, електрон, що рухається прискорено, повинен випромінювати електромагнітні хвилі, втрачати енергію і кінець кінцем впасти на ядро. Але атом – стійка система електричних зарядів. І тому, приймаючи ядерну модель атома, потрібно відмовитись від класичного опису орбітального руху електронів.
Перший крок в цьому напрямку зробив Н. Бор (1913 р.), сформулювавши наступні постулати:
а) із усіх можливих механічних станів (орбіт) електрона в атомі здійснюються лише такі, для яких момент імпульсу орбітального руху електрона кратний до постійної Планка h, тобто
![]() , (6.1)
, (6.1)
де ![]() – квантове число стану (номер орбіти), а
– квантове число стану (номер орбіти), а ![]() – постійна Дірака; такі стани (орбіти) називаються стаціонарними;
– постійна Дірака; такі стани (орбіти) називаються стаціонарними;
б) перебуваючи в стаціонарному стані, електрон атома не випромінює і не поглинає енергії;
в) при переході з одного стаціонарного стану на інший (мал.6.1) електрон випромінює (поглинає) квант світла з енергією, рівною різниці енергій цих станів, тобто
![]() . (6.2)
. (6.2)
Отже, основна ідея постулатів Бора полягає в квантуванні (дискретності) механічних характеристик руху електронів в атомі (моменту імпульса, енергії тощо) і в стрибкоподібній зміні цих характеристик.
Вперше ядерна модель атома з постулатами Бора була застосована до воднеподібних атомів ![]() тощо), в яких навколо ядра рухається по коловій орбіті радіусом r лише один електрон. При цьому ядро вважається нерухомим, а електрон розглядається як класична матеріальна точка. Враховуючи, що в ролі доцентрової сили виступає кулонівська сила взаємодії між електроном та ядром, тобто
тощо), в яких навколо ядра рухається по коловій орбіті радіусом r лише один електрон. При цьому ядро вважається нерухомим, а електрон розглядається як класична матеріальна точка. Враховуючи, що в ролі доцентрової сили виступає кулонівська сила взаємодії між електроном та ядром, тобто ![]() , і вираз (6.1), отримаємо для радіуса стаціонарної орбіти електрона вираз
, і вираз (6.1), отримаємо для радіуса стаціонарної орбіти електрона вираз
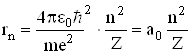 , (6.3)
, (6.3)
де ![]() – борівський радіус, який має зміст радіуса першої (
– борівський радіус, який має зміст радіуса першої (![]() орбіти електрона в атомі водню (
орбіти електрона в атомі водню (![]() . Отже, має місце квантування радіусів стаціонарних орбіт електрона, оскільки
. Отже, має місце квантування радіусів стаціонарних орбіт електрона, оскільки ![]() .
.
Для повної механічної енергії електрона ![]() легко отримати вираз
легко отримати вираз
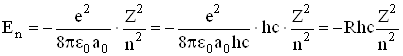 , (6.4)
, (6.4)
де ![]() – постійна Рідберга.
– постійна Рідберга.
Отже, енергія воднеподібних атомів в стаціонарних станах приймає дискретні значення, тобто квантується. Стан з найнижчою енергією ![]() називається основним, усі інші стани – збудженими. Стан з найвищою енергією
називається основним, усі інші стани – збудженими. Стан з найвищою енергією ![]() відповідає іонізації атома. Отже, енергія іонізації воднеподібних атомів
відповідає іонізації атома. Отже, енергія іонізації воднеподібних атомів
![]() , (еВ).
, (еВ).
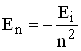 . (6.5)
. (6.5)
Зобразимо енергетичну діаграму борівського атома водню (![]() (мал.6.2). В основному стані атом може перебувати як завгодно довго. Якщо ж його перевести певним чином (теплом, світлом, ударом вільних електронів тощо) в збуджений стан, то тривалість перебування в цьому стані складає
(мал.6.2). В основному стані атом може перебувати як завгодно довго. Якщо ж його перевести певним чином (теплом, світлом, ударом вільних електронів тощо) в збуджений стан, то тривалість перебування в цьому стані складає ![]() , і атом самовільно переходить в основний чи нижчі збуджені стани (мал.6.2), випромінюючи фотони з енергіями
, і атом самовільно переходить в основний чи нижчі збуджені стани (мал.6.2), випромінюючи фотони з енергіями
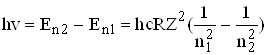 .
.
Довжини випромінюваних світлових хвиль розраховуються за серіальною формулою Бальмера:
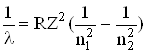 , (6.6)
, (6.6)
де n2 – квантове число стану, з якого відбувається перехід, n1 – квантове число стану, в який переходить атом.
Усі спектральні лінії можна згрупувати в наступні серії: І–серія Лаймана (![]() n2
n2![]() ; ІІ–серія Бальмера (
; ІІ–серія Бальмера (![]()
![]() ІІІ–серія Пашена (
ІІІ–серія Пашена (![]()
![]() тощо. Лінії серії Лаймана лежать в ультрафіолетовій області, серії Бальмера – у видимій області, серії Пашена – в інфрачервоній області.
тощо. Лінії серії Лаймана лежать в ультрафіолетовій області, серії Бальмера – у видимій області, серії Пашена – в інфрачервоній області.
Теорія Бора дуже добре описала положення спектральних ліній випромінювання воднеподібних атомів, але виявилась нездатною пояснити спектри випромінювання складних атомів, а також інтенсивності спектральних ліній навіть атомарного водню. Слабкість цієї теорії зумовлена її непослідовністю: вона – напівкласична, напівквантова.
§ 6.2. Корпускулярно-хвильовий дуалізм матерії; гіпотеза де Бройля. Співвідношення невизначеностей Гайзенберга
В 1924 р. Луі де Бройль висунув гіпотезу (постулат) про те, що корпускулярно-хвильовий дуалізм притаманний не тільки світлу, як це показано в розділі V, але матерії взагалі: усяка частинка, яка має імпульс ![]() і енергію Е, володіє хвильовими властивостями, її рух супроводжується хвильовим процесом з довжиною хвилі де Бройля
і енергію Е, володіє хвильовими властивостями, її рух супроводжується хвильовим процесом з довжиною хвилі де Бройля
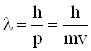 (6.7)
(6.7)
та частотою ![]() . (6.8)
. (6.8)
В залежності від величини швидкості v (чи кінетичної енергії Т) частинок, їх імпульс розраховується або за класичною формулою (при v<<c, T<<E0)
![]() , (6.9)
, (6.9)
або за релятивістською формулою (при ![]() , Т співмірна з Е0)
, Т співмірна з Е0)
![]() , (6.10)
, (6.10)
де m0 – маса спокою частинки (таблична величина), ![]()
![]() – її енергія спокою.
– її енергія спокою.
Відомо, що хвильові властивості світла найбільш чітко проявляються в явищі дифракції. І тому прояву хвильових властивостей електронних (нейтронних, атомних тощо) пучків слід очікувати в цьому явищі, при якому чітка дифракційна картина спостерігатиметься, коли довжина хвилі співмірна з розміром дифракційної неоднорідності.
Оцінимо довжину хвилі де Бройля електронів, які прискорились відносно слабким електричним полем (![]() . Саме такі напруги використовуються у вакуумних електронних приладах (радіолампи, ЕПТ, рентгенівські трубки тощо). Підставляючи в (6.9) значення кінетичної енергії
. Саме такі напруги використовуються у вакуумних електронних приладах (радіолампи, ЕПТ, рентгенівські трубки тощо). Підставляючи в (6.9) значення кінетичної енергії ![]() еВ, отримаємо за (6.7) значення довжин хвиль де Бройля
еВ, отримаємо за (6.7) значення довжин хвиль де Бройля ![]() нм. Оскільки розміри макроприладів значно більші від
нм. Оскільки розміри макроприладів значно більші від ![]() , то хвильові властивості електронів в цьому випадку не відслідковуються. В цей же час розраховані значення
, то хвильові властивості електронів в цьому випадку не відслідковуються. В цей же час розраховані значення ![]() співмірні з розміром кристалічної гратки (
співмірні з розміром кристалічної гратки (![]() нм) твердих тіл. І тому така гратка повинна бути дифракційним пристроєм для електронних пучків. Дійсно, при проходженні електронних пучків через тонкі полікристалічні металічні плівки та при їх відбиванні від монокристалів спостерігається дифракційна картина, така ж як і у випадку рентгенівських променів.
нм) твердих тіл. І тому така гратка повинна бути дифракційним пристроєм для електронних пучків. Дійсно, при проходженні електронних пучків через тонкі полікристалічні металічні плівки та при їх відбиванні від монокристалів спостерігається дифракційна картина, така ж як і у випадку рентгенівських променів.
Відмітимо, що довжина хвиль де Бройля рухомих макротіл, за рахунок великої маси, настільки мала, що їх хвильову природу виявити неможливо.
В класичній механіці стан частинки задається сукупністю точно заданих координат (x,y,z) та проекцій вектора імпульсу (рх, рy, рz). Зокрема, для одновимірного випадку неточності (невизначеності) координати (![]() та імпульсу (
та імпульсу (![]() рівні нулю, і тому:
рівні нулю, і тому: ![]() .
.
Корпускулярно-хвильовий дуалізм частинок в мікросвіті накладає обмеження на можливості класичного опису. Дійсно, вільна частинка, що рухається вздовж осі х, описується плоскою монохроматичною хвилею де Бройля
![]() , (6.11)
, (6.11)
де ![]() – її циклічна частота,
– її циклічна частота, ![]() – її хвильове число. В цьому випадку
– її хвильове число. В цьому випадку ![]() , і тому положення частинки повністю невизначене:
, і тому положення частинки повністю невизначене: ![]() . З іншого боку, імпульс такої частинки (
. З іншого боку, імпульс такої частинки (![]() строго визначений, бо
строго визначений, бо ![]() і
і ![]() . А отже, добуток
. А отже, добуток ![]() є математично невизначеним (
є математично невизначеним (![]() .
.
В мікросвіті можна змоделювати об’єкти (наприклад, хвильовий пакет), для яких координата точно визначена (![]() , але імпульс повністю невизначений (
, але імпульс повністю невизначений (![]() , і тому має місце математична невизначеність типу
, і тому має місце математична невизначеність типу ![]()
Аналізуючи умовні експерименти, пов’язані з проходженням мікрочастинок через щілини, Гайзенберг (1927 р.) встановив наступні співвідношення між невизначеностями координат та відповідних імпульсів мікрочастинок
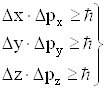 . (6.12)
. (6.12)
Інтерпретацію цих співвідношень дав Н. Бор у вигляді принципу доповнюваності:
1) інформація про стан мікрочастинок може бути отримана лише за допомогою макроприладів, які взаємодіють з мікрочастинками;
2) за допомогою конкретного макроприладу можна встановити точне значення або координати, або імпульсу; при цьому чим точніше встановлена одна характеристика, тим невизначеніша інша.
Із співвідношення Гайзенберга слідує, зокрема, що поняття електронної орбіти в атомі втрачає зміст. Дійсно, якщо невизначеність швидкості електрона співмірна з самою швидкістю, тобто ![]() , то невизначеність координати
, то невизначеність координати ![]() , що співмірно з розміром атома. А отже, електрон “розмазаний” по всьому об’ємі атома.
, що співмірно з розміром атома. А отже, електрон “розмазаний” по всьому об’ємі атома.
Пара “координата-імпульс” у співвідношенні (6.12) не є випадковою, оскільки вона входить як добуток в рівняння плоскої хвилі де Бройля (6.11), представлене у вигляді
![]() . (6.13)
. (6.13)
І тому слід очікувати, що і для іншої пари “енергія-час” матиме місце співвідношення невизначеності
![]() , (6.14)
, (6.14)
де ![]() має зміст тривалості перебування (часу життя) мікрочастинки в певному стані. Зокрема, для основного стану електрона у воднеподібному атомі
має зміст тривалості перебування (часу життя) мікрочастинки в певному стані. Зокрема, для основного стану електрона у воднеподібному атомі ![]() і тому
і тому ![]() , тобто енергетичний рівень основного стану нерозмитий.
, тобто енергетичний рівень основного стану нерозмитий.
§ 6.3. Хвильова функція та її зміст. Рівняння Шрьодінгера
Корпускулярно-хвильовий дуалізм матерії встановлює межі застосування класичної механіки, і для опису мікросвіту використовуються закони квантової механіки, в якій стан мікрочастинок задається вже не координатами та імпульсами, а хвильовою функцією ![]() . Зокрема, для вільної одновимірної частинки хвильовою функцією є плоска хвиля де Бройля, яку представимо тут у комплексній формі:
. Зокрема, для вільної одновимірної частинки хвильовою функцією є плоска хвиля де Бройля, яку представимо тут у комплексній формі:
![]() , (6.15)
, (6.15)
де ![]() . Помноживши
. Помноживши ![]() на комплексно спряжену функцію
на комплексно спряжену функцію ![]() , отримаємо
, отримаємо
![]() .
.
З точки зору хвильових уявлень квадрат амплітуди хвилі визначає її інтенсивність; з точки зору корпускулярних уявлень – це ймовірність виявити мікрочастинку в певній області простору. Отже, фізичний зміст має не сама хвильова функція, а вираз ![]() , який називається густиною імовірності. Імовірність знайти частинку в елементарному об’ємі
, який називається густиною імовірності. Імовірність знайти частинку в елементарному об’ємі ![]() становить
становить
![]() . (6.16)
. (6.16)
Для частинок, які не є вільними, хвильова функція не представляється хвилею де Бройля, але її ймовірнісна інтерпретація залишається в силі.
Оскільки імовірність повинна бути однозначною, неперервною і скінченною, то на хвильову функцію накладаються наступні стандартні вимоги:
1) вона повинна бути однозначною, неперервною і скінченною;
2) перші похідні від хвильової функції по координатах і часу також повинні бути неперервними, що забезпечить “гладкість” імовірності;
3) вона повинна бути інтегрованою; зокрема, 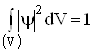 , як імовірність знайти частинку в будь-якій точці простору V (імовірність вірогідної події).
, як імовірність знайти частинку в будь-якій точці простору V (імовірність вірогідної події).
Для знаходження хвильової функції конкретного квантовомеханічного об’єкту необхідно розв’язати рівняння Шрьодінгера (1926 р.)
![]() , (6.17)
, (6.17)
яке є аналогом ІІ закону Ньютона класичної механіки. В цьому рівнянні
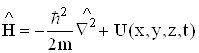 – (6.18)
– (6.18)
оператор Гамільтона або оператор повної енергії частинки, де m – маса частинки, ![]() – оператор Лапласа:
– оператор Лапласа:
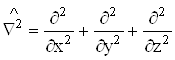 , (6.19)
, (6.19)
U – оператор потенціальної енергії, дія якого зводиться до простого множення на хвильову функцію.
Якщо потенціальна енергія частинки явно не залежить від часу, тобто ![]() , то квантовомеханічна задача називається стаціонарною. І хвильову функцію можна представити у вигляді
, то квантовомеханічна задача називається стаціонарною. І хвильову функцію можна представити у вигляді ![]() .
.
Координатнозалежну складову хвильової функції знаходять із розв’язку рівняння Шрьодінгера для стаціонарних станів
![]() , (6.20)
, (6.20)
де параметр Е має зміст енергії частинки.
Розв’язок цього диференційного рівняння задовільняє стандартні вимоги до хвильової функції, як правило, не при усяких, а дозволених (дискретних) значеннях параметра Е. Ці значення Е називаються власними значеннями оператора ![]() , а відповідні хвильові функції
, а відповідні хвильові функції ![]() – власними функціями цього оператора. В кожному конкретному випадку потрібно задати аналітичну форму оператора
– власними функціями цього оператора. В кожному конкретному випадку потрібно задати аналітичну форму оператора ![]() (6.18), тобто побудувати потенціальну модель квантомеханічного об’єкту.
(6.18), тобто побудувати потенціальну модель квантомеханічного об’єкту.
§6.4. Частинка в одновимірній прямокутній потенціальній ямі (ящику). Проходження частинки через потенціальний бар’єр
Усякий зв’язаний стан частинки (електрон в атомі, вільний електрон в металі, нуклон в ядрі тощо), тобто стан з від’ємною потенціальною енергією, можна описати поняттям потенціальної ями.
Розглянемо найпростіший випадок, коли частинка масою m перебуває в одновимірній прямокутній нескінченно глибокій потенціальній ямі шириною l .Оскільки початок відліку потенціальної енергії можна вибирати довільно, то задачу про “яму” замінимо задачею про “ящик”, на дні якого потенціальна енергія дорівнює нулю, а стінки якого нескінченно високі (мал.6.3). Оператор Гамільтона ![]() (6.18) для цього випадку має вигляд
(6.18) для цього випадку має вигляд
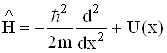 , (6.21)
, (6.21)
де ![]()
![]()
![]()
![]()
![]()
Всередині ящика рівняння Шрьодінгера запишеться як
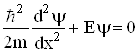 . (6.22)
. (6.22)
Розв’язок цього рівняння, з врахуванням стандартних вимог, зокрема, ![]() , має вигляд
, має вигляд
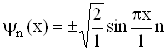 , (6.23)
, (6.23)
де n=1,2,3,… – квантове число стану частинки. Енергія частинки в різних квантових станах
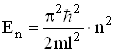 , (6.24)
, (6.24)
тобто приймає не довільні, а дискретні значення Е1, Е2, Е3, …, зображені на мал.6.3 відповідними енергетичними рівнями. Густина імовірності ![]() залежить від координати частинки, при цьому по різному в кожному квантовому стані.
залежить від координати частинки, при цьому по різному в кожному квантовому стані.
Відстань між сусідніми енергетичними рівнями
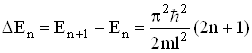 . (6.25)
. (6.25)
Зокрема, для електрона в ямі шириною l![]() , яка співмірна з розміром атома, отримаємо
, яка співмірна з розміром атома, отримаємо ![]() В цей же час для макрооб’єктів, коли m i l – дуже великі, відстань між рівнями стає зникаюче малою, і тому квантуванням енергії можна знехтувати. Задача про частинку в потенціальній ямі скінченної глибини має дещо складніший розв’язок, але висновок про квантування енергії залишається в силі і в цьому випадку.
В цей же час для макрооб’єктів, коли m i l – дуже великі, відстань між рівнями стає зникаюче малою, і тому квантуванням енергії можна знехтувати. Задача про частинку в потенціальній ямі скінченної глибини має дещо складніший розв’язок, але висновок про квантування енергії залишається в силі і в цьому випадку.
Спорідненою до описаної є задача про проходження частинки через потенціальний бар’єр шириною l і висотою U0 (мал.6.4). Якщо частинка класична, то вона пролітає над бар’єром, коли Е>U0, і відбивається від нього, коли Е<U0, бо проникнення під бар’єр означало б, що її кінетична енергія від’ємна.
Для квантовомеханічної мікро-частинки розв’язок рівняння Шрьодінгера дає, що хвильові функції в усіх трьох областях (![]() відмінні від нуля, тобто мікрочастинка проникає під бар’єр і за бар’єр. Це явище називається тунелюванням. Від’ємні значення кінетичної енергії в області ІІ не можуть турбувати, бо в квантовій механіці, в силу дії співвідношення Гайзенберга (§ 6.2), кінетична енергія
відмінні від нуля, тобто мікрочастинка проникає під бар’єр і за бар’єр. Це явище називається тунелюванням. Від’ємні значення кінетичної енергії в області ІІ не можуть турбувати, бо в квантовій механіці, в силу дії співвідношення Гайзенберга (§ 6.2), кінетична енергія ![]() , як і потенціальна енергія U(x), не є точно визначеними. Прозорість бар’єру
, як і потенціальна енергія U(x), не є точно визначеними. Прозорість бар’єру ![]() тим більша, чим менша його ширина і висота, а також, чим менша маса частинки, тобто ефект тунелювання помітний лише в мікросвіті.
тим більша, чим менша його ширина і висота, а також, чим менша маса частинки, тобто ефект тунелювання помітний лише в мікросвіті.
§ 6.5. Квантовий лінійний гармонічний осцилятор
Лінійний гармонічний осцилятор – це матеріальна точка, яка здійснює рух вздовж осі х під дією квазіпружної сили ![]() . Потенціальна енергія осцилятора (мал.6.5):
. Потенціальна енергія осцилятора (мал.6.5):
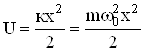 , (6.26)
, (6.26)
де m – маса осцилятора, ![]() – його власна циклічна частота, х – зміщення від положення рівноваги. Підставляючи (6.26) в рівняння Шрьодінгера (6.20), отримаємо
– його власна циклічна частота, х – зміщення від положення рівноваги. Підставляючи (6.26) в рівняння Шрьодінгера (6.20), отримаємо
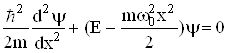 . (6.27)
. (6.27)
Розв’язок цього рівняння, виражений через поліноми Чебишева-Ерміта, задовільняє стандартні вимоги до хвильових функцій лише тоді, коли енергія осцилятора квантується за законом
![]() , (6.28)
, (6.28)
де ![]() =0,1,2,… – коливальне квантове число.
=0,1,2,… – коливальне квантове число.
Відмітимо, що найменша енергія квантового осцилятора при ![]() =0, так звана нульова енергія, на відміну від класичного осцилятора не дорівнює нулю. Наявність нульових коливань підтверджується експериментально фактом розсіяння світла кристалами при дуже низьких температурах.
=0, так звана нульова енергія, на відміну від класичного осцилятора не дорівнює нулю. Наявність нульових коливань підтверджується експериментально фактом розсіяння світла кристалами при дуже низьких температурах.
Перебуваючи в певному квантовому стані, осцилятор не поглинає і не випромінює енергії. Випромінювання (поглинання) енергії відбувається при переході осцилятора між квантовими станами, при цьому дозволяються (правила відбору) переходи лише між сусідніми енергетичними рівнями (мал.6.5), тобто ![]() . Енергія випромінюваного (поглинутого) кванту
. Енергія випромінюваного (поглинутого) кванту ![]() , що підтверджує квантовий постулат Планка.
, що підтверджує квантовий постулат Планка.
§ 6.6. Воднеподібні атоми в квантовій механіці. Квантові числа електрона в атомі
Потенціальна енергія електрона в кулонівському полі ядра воднеподібного атома має вигляд
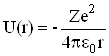 , (6.29)
, (6.29)
де r – відстань від центру ядра.
З врахуванням (6.29) стаціонарне рівняння Шрьодінгера (6.20) запишеться як
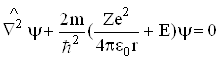 . (6.30)
. (6.30)
Оскільки кулонівське поле володіє центральною симетрією, то зручно перейти до сферичних координат, де положення довільної точки описується однією лінійною координатою (r) і двома кутовими (![]() . В цьому випадку у хвильовій функції електрона можна провести розділення змінних:
. В цьому випадку у хвильовій функції електрона можна провести розділення змінних:
![]() .
.
Стандартні вимоги як до хвильової функції в цілому, так і до окремих складових виконуються лише при певних (дискретних) значеннях не тільки енергії електрона Еn, але і квадрату моменту імпульсу його орбітального руху ![]() , а також проекції цього моменту
, а також проекції цього моменту ![]() на вибраний напрямок (вісь z). Квантування вказаних характеристик визначається трьома квантовими числами: головним n, орбітальним (азімутальним)
на вибраний напрямок (вісь z). Квантування вказаних характеристик визначається трьома квантовими числами: головним n, орбітальним (азімутальним) ![]() та магнітним
та магнітним ![]() наступним чином:
наступним чином:
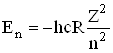 , (6.31)
, (6.31)
де n=1,2,3,…; відмітимо, що (6.31) співпадає з (6.4) для борівського воднеподібного атома;
![]() , (6.32)
, (6.32)
де ![]() =0,1,2,…, n-1;
=0,1,2,…, n-1;
![]() , (6.33)
, (6.33)
де ![]() =0,
=0,![]() .
.
Оскільки енергія електрона Еn визначається лише головним квантовим числом n, а хвильова функція ![]() – трьома квантовими числами, то декільком станам з різними
– трьома квантовими числами, то декільком станам з різними ![]() та
та ![]() відповідає одне значення енергії. Така ситуація називається квантовомеханічним виродженням. Наприклад, енергія Е2 реалізується в чотирьох станах з хвильовими функціями
відповідає одне значення енергії. Така ситуація називається квантовомеханічним виродженням. Наприклад, енергія Е2 реалізується в чотирьох станах з хвильовими функціями ![]()
![]()
![]()
![]() . В загальному, кратність виродження дорівнює n2 . Традиційно, стани з різними
. В загальному, кратність виродження дорівнює n2 . Традиційно, стани з різними ![]() позначаються наступними буквами:
позначаються наступними буквами:
![]() : 0, 1, 2, 3, …
: 0, 1, 2, 3, …
стан: s, p, d, f, …
Для попереднього прикладу енергія Е2 реалізується в станах 2s i 2p.
Основний стан (1s) є невиродженим і описується хвильовою функцією
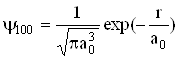 . (6.34)
. (6.34)
Для цього стану імовірність перебування електрона в сферичному шарі одиничної товщини на відстані r від центру ядра
![]() ~
~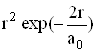 . (6.35)
. (6.35)
Як видно з мал.6.6, де представлена залежність ![]() , максимальна імовірність реалізується на відстанях, рівних борівському радіусу а0 . Отже, борівські траєкторії можна інтерпретувати в квантовій механіці як геометричне місце точок з максимальною імовірністю перебування електрона. Хоч в дійсності його заряд “розмазаний” по всьому об’єму атома.
, максимальна імовірність реалізується на відстанях, рівних борівському радіусу а0 . Отже, борівські траєкторії можна інтерпретувати в квантовій механіці як геометричне місце точок з максимальною імовірністю перебування електрона. Хоч в дійсності його заряд “розмазаний” по всьому об’єму атома.
§ 6.7. Власний момент (спін) електрона. Принцип Паулі. Забудова складних атомів. Характеристичне рентгенівське випромінювання
Орбітальний рух електрона в атомі можна розглядати як коловий струм, з яким пов’язаний магнітний момент ![]() . Проекція цього моменту на вибраний напрямок, який задається магнітним полем індукцією В,
. Проекція цього моменту на вибраний напрямок, який задається магнітним полем індукцією В,
 , (6.36)
, (6.36)
де mел – маса електрона, ![]() – магнітне квантове число. В s-стані
– магнітне квантове число. В s-стані ![]() =0, і тому такий електрон не повинен володіти магнітним моментом, що суперечить ряду експериментальних спостережень. І тому була висунута
=0, і тому такий електрон не повинен володіти магнітним моментом, що суперечить ряду експериментальних спостережень. І тому була висунута
(1925 р.) гіпотеза про те, що електрони володіють власним, не пов’язаним з просторовим переміщенням, моментом імпульсу і відповідним магнітним моментом. Ця властивість електронів була названа спіном. Спіновий момент імпульсу електрона визначається формулою
![]() , (6.37)
, (6.37)
де s – cпінове квантове число, рівне ![]() .
.
Проекція цього моменту на вибраний напрямок (наприклад, напрямок магнітного поля)
![]() , (6.38)
, (6.38)
де ms=![]() –магнітне спінове число.
–магнітне спінове число.
Пізніше виявилось, що спіном володіють усі мікрочастинки. При цьому частинки з напівцілим спіном ![]()
![]()
![]() утворюють клас ферміонів (електрони, протони, нейтрони тощо), а частинки з цілим спіном (s=0,1,…) утворюють клас бозонів (фотони, мезони тощо). Для ферміонів справедливий принцип Паулі: два тотожні ферміони не можуть одночасно перебувати в однаковому стані.
утворюють клас ферміонів (електрони, протони, нейтрони тощо), а частинки з цілим спіном (s=0,1,…) утворюють клас бозонів (фотони, мезони тощо). Для ферміонів справедливий принцип Паулі: два тотожні ферміони не можуть одночасно перебувати в однаковому стані.
В багатоелектронних атомах стан кожного електрона описується четвіркою квантових чисел: n, ![]() ,
, ![]() , ms. Принцип Паулі в цьому випадку гласить: в атомі не може бути двох електронів з ідентичним набором чотирьох квантових чисел. Електрони, які мають однакове головне квантове число n, утворюють шар. Максимальна кількість електронів у шарі визначається формулою 2n2. Класифікація шарів: К(n=1), L(n=2), M(n=3), N(n=4) тощо. Електрони з однаковими квантовими числами n i
, ms. Принцип Паулі в цьому випадку гласить: в атомі не може бути двох електронів з ідентичним набором чотирьох квантових чисел. Електрони, які мають однакове головне квантове число n, утворюють шар. Максимальна кількість електронів у шарі визначається формулою 2n2. Класифікація шарів: К(n=1), L(n=2), M(n=3), N(n=4) тощо. Електрони з однаковими квантовими числами n i ![]() утворюють оболонку. Максимальна кількість електронів в оболонці визначається формулою 2(2
утворюють оболонку. Максимальна кількість електронів в оболонці визначається формулою 2(2![]() +1). Класифікація оболонок: s(
+1). Класифікація оболонок: s(![]() =0), p(
=0), p(![]() =1), d(
=1), d(![]() =2), f(
=2), f(![]() =3) тощо.
=3) тощо.
При забудові електронами шарів і оболонок, крім принципу Паулі, необхідно врахувати принцип мінімальності енергії. Це означає, що забудова починається з шарів і оболонок, де енергія електронів найменша. У воднеподібних атомах енергія електрона залежить лише від головного квантового числа n. В складних атомах на окремий електрон діє поле не тільки ядра, але і решти електронів. Це приводить до того, що виродження по ![]() знімається, і енергія починає залежати як від n, так і від
знімається, і енергія починає залежати як від n, так і від ![]() . Але, як правило, залежність від n сильніша. І тому заповнення починається з глибоких шарів. Наприклад, електронна конфігурація атома міді має наступний вигляд (цифри над символами вказують на кількість електронів в оболонках): 1s2 2s2 2p6 3s2 3p6 3d10 4s1. Видно, що оболонки шарів K, L, M повністю заповнені, і лише оболонка 4s заповнена частково. Відмітимо, що повні моменти імпульсів як орбітального, так і спінового рухів електронів заповнених оболонок рівні нулю. І тому стан атома визначається електронами частково заповненої оболонки; такі електрони називаються валентними. В нашому прикладі атом міді має один валентний електрон в s-стані. Саме валентні електрони забезпечують хімічний зв’язок між атомами в молекулах і в кристалічній гратці твердих тіл. Вони відповідальні за спектри випромінювання та поглинання атомів.
. Але, як правило, залежність від n сильніша. І тому заповнення починається з глибоких шарів. Наприклад, електронна конфігурація атома міді має наступний вигляд (цифри над символами вказують на кількість електронів в оболонках): 1s2 2s2 2p6 3s2 3p6 3d10 4s1. Видно, що оболонки шарів K, L, M повністю заповнені, і лише оболонка 4s заповнена частково. Відмітимо, що повні моменти імпульсів як орбітального, так і спінового рухів електронів заповнених оболонок рівні нулю. І тому стан атома визначається електронами частково заповненої оболонки; такі електрони називаються валентними. В нашому прикладі атом міді має один валентний електрон в s-стані. Саме валентні електрони забезпечують хімічний зв’язок між атомами в молекулах і в кристалічній гратці твердих тіл. Вони відповідальні за спектри випромінювання та поглинання атомів.
Зрозуміло, що переходи між енергетичними рівнями повністю заповнених шарів і оболонок неможливі. Але така можливість з’являється, якщо певним чином вибити електрон з глибокого шару, наприклад, при бомбардуванні металічного анода (антикатода) рентгенівської трубки швидкими електронами. В цьому випадку на вакантне місце глибокого шару може перейти електрон вищого шару. При такому переході випромінюється фотон з енергією ![]() , у відповідності з енергетичною діаграмою (мал.6.7), на якій кожен шар зображений одним енергетичним рівнем. (В дійсності всі шари, крім К-шару, володіють декількома близькими рівнями, бо енергія залежить як від головного квантового числа n, так і від орбітального квантового числа
, у відповідності з енергетичною діаграмою (мал.6.7), на якій кожен шар зображений одним енергетичним рівнем. (В дійсності всі шари, крім К-шару, володіють декількома близькими рівнями, бо енергія залежить як від головного квантового числа n, так і від орбітального квантового числа ![]() ).
).
Оскільки відстань між енергетичними рівнями глибоких шарів дуже велика (![]() , то довжини хвиль випромінюваних фотонів
, то довжини хвиль випромінюваних фотонів ![]() , що відповідає рентгенівському діапазону. Зрозуміло, що спектр такого випромінювання, яке називають характеристичним, – дискретний. Спектральні лінії характеристичного рентгенівського випромінювання групуються в серії: K, L, М, N – серії. Наприклад, К-серія формується при переході електронів на вакантне місце в К-шари (n1=1) з шарів L, M, N, …(n2=2, 3, 4, …) – відповідно:
, що відповідає рентгенівському діапазону. Зрозуміло, що спектр такого випромінювання, яке називають характеристичним, – дискретний. Спектральні лінії характеристичного рентгенівського випромінювання групуються в серії: K, L, М, N – серії. Наприклад, К-серія формується при переході електронів на вакантне місце в К-шари (n1=1) з шарів L, M, N, …(n2=2, 3, 4, …) – відповідно: ![]() – лінії. Довжини хвиль спектральних ліній в серіях описуються формулою Мозлі
– лінії. Довжини хвиль спектральних ліній в серіях описуються формулою Мозлі
![]()
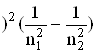 , (6.39)
, (6.39)
де R – постійна Рідберга (§ 6.1), ![]() – постійна екранування (
– постійна екранування (![]()
![]() для К-серії). Ця формула переходить у формулу Бальмера (6.6), якщо покласти
для К-серії). Ця формула переходить у формулу Бальмера (6.6), якщо покласти ![]() . Постійна екранування враховує цю обставину, що “випромінюючий” електрон перебуває не тільки в кулонівському полі ядра, як це мало місце у воднеподібних атомах, але і в екрануючому полі інших електронів складних атомів.
. Постійна екранування враховує цю обставину, що “випромінюючий” електрон перебуває не тільки в кулонівському полі ядра, як це мало місце у воднеподібних атомах, але і в екрануючому полі інших електронів складних атомів.
§ 6.8. Теплові коливання кристалічної гратки і теплоємність твердих тіл
Більшість твердих тіл володіють кристалічною структурою, тобто є сукупністю великого числа атомів, впорядковано розміщених в просторі, і які тим самим утворюють кристалічну гратку. Оскільки атоми, що перебувають в сусідніх вузлах кристалічної гратки, зазнають взаємного притягання і відштовхування, то потенціальна енергія взаємодії між ними має вигляд потенціальної ями (мал.6.8).
В рамках класичної фізики при абсо-лютному нулю атоми повинні перебувати на дні потенціальної ями, на відстані r0 один від іншого. І, звичайно, бути нерухомими. З підвищенням температури енергія атомів зростає, і кожен атом починає здійснювати коливний рух відносно рівноважного положення між точками А і В. При дуже низьких температурах ці коливання можна вважати гармонічними, бо залежність Ер(r) – приблизно параболічна. При вищих температурах, як видно з мал.6.8, з’являється асиметрія відхилень від рівноважного положення r0: коливання стають ангармонічними. За рахунок ангармонізму середня відстань між атомами з ростом температури збільшується – має місце теплове розширення твердих тіл.
Оскільки три взаємноперпендикулярні напрямки коливань є рівноправними, то можна вважати, що атом в кристалічній гратці володіє трьома коливними ступенями вільності (і=3). Якщо знехтувати ефектом ангармонізму, то теплові коливання окремого атома можна моделювати сукупністю трьох незалежних лінійних осциляторів. Будемо вважати коливання окремих атомів незалежними. Тоді для одного моля речовини кількість ступенів вільності коливного руху складатиме 3NA, де NA – число Авогадро. В класичній фізиці на одну ступінь вільності коливного руху припадає енергія к0Т, де к0 – постійна Больцмана. Отже, внутрішня енергія моля твердого тіла
![]() , (6.40)
, (6.40)
де R – універсальна газова стала.
Молярна теплоємність тіла
![]() . (6.41)
. (6.41)
Такий результат (закон Дюлонга-Пті) підтверджується експериментально для багатьох простих кристалічних речовин при високих температурах. Але при низьких температурах експеримент (мал.6.9) і класична теорія катастрофічно розходяться. Зокрема, при дуже низьких температурах виконується “закон кубів Дебая” , у відповідності з яким ![]() .
.
Першу спробу узгодити експери-мент з теорією здійснив А. Ейнштейн
(1907 р.), який залишивши тезу про незалежність осциляторів, запропонував вважати останні не класичними, а квантовими.
Як показано в § 6.5, енергія квантового лінійного осцилятора
![]() . (6.42)
. (6.42)
Ейнштейн припустив, що всі осцилятори коливаються з однаковою частотою ![]() , а їх розподіл за енергією описується класичною функцією розподілу Максвелла-Больцмана
, а їх розподіл за енергією описується класичною функцією розподілу Максвелла-Больцмана
 , (6.43)
, (6.43)
де N0 – загальна кількість атомів, а N![]() – кількість атомів, коливна енергія яких складає
– кількість атомів, коливна енергія яких складає ![]() . Тоді середня енергія одного осцилятора, тобто енергія, що припадає на одну ступінь вільності,
. Тоді середня енергія одного осцилятора, тобто енергія, що припадає на одну ступінь вільності,
 . (6.44)
. (6.44)
Після математичних перетворень останній вираз запишеться як
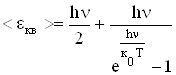 . (6.45)
. (6.45)
Внутрішня енергія одного моля твердого тіла
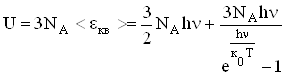 ,
,
а молярна теплоємність
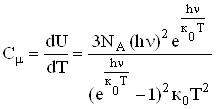 . (6.46)
. (6.46)
При високих температурах, коли к0Т>>h![]() , формула (6.46) дає
, формула (6.46) дає ![]() , тобто закон Дюлонга-Пті. При низьких температурах, коли к0Т<<h
, тобто закон Дюлонга-Пті. При низьких температурах, коли к0Т<<h![]() , отримаємо
, отримаємо
 . (6.47)
. (6.47)
Оскільки експоненційна залежність сильніша від степеневої, то (6.47) дає зменшення теплоємності з пониженням температури, що лише якісно узгоджується з експериментом (мал.6.9), але не забезпечує кількісно виконання “закону кубів Дебая”. Для розділення областей високотемпературного і низькотемпературного наближень вводиться характеристична температура Ейнштейна ![]() , при якій
, при якій ![]() ; звідси
; звідси 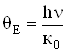 . Отже, при
. Отже, при ![]() виконується закон Дюлонга-Пті; при
виконується закон Дюлонга-Пті; при ![]() виконується залежність (6.47).
виконується залежність (6.47).
Подальше удосконалення теорії, здійснене Дебаєм (1912 р.), полягає в тому, що коливання атомів кристалічної гратки вже не вважаються незалежними; в кристалі встановлюється система т.з. нормальних коливань з частотою від 0 до ![]() ; при цьому в коливанні певної частоти беруть участь всі атоми гратки. Розглядаючи кожне коливання як квантовий лінійний осцилятор, після математичних перетворень отримаємо для внутрішньої енергії моля твердого тіла
; при цьому в коливанні певної частоти беруть участь всі атоми гратки. Розглядаючи кожне коливання як квантовий лінійний осцилятор, після математичних перетворень отримаємо для внутрішньої енергії моля твердого тіла
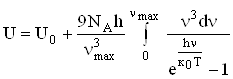 ,
,
а для молярної теплоємності ![]() , ввівши позначення
, ввівши позначення 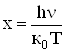 ,
,
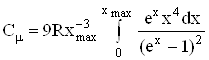 . (6.48)
. (6.48)
За аналогією з попереднім введемо характеристичну температуру Дебая ![]() , використавши співвідношення
, використавши співвідношення ![]() ; звідси
; звідси
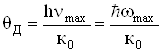 . (6.49)
. (6.49)
Оскільки ![]() , то (6.48) після інтегрування набуде вигляду
, то (6.48) після інтегрування набуде вигляду
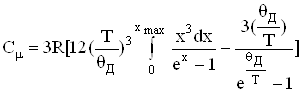 . (6.50)
. (6.50)
При високих температурах (Т>>![]() ), коли х
), коли х![]() , використавши наближення
, використавши наближення ![]() , отримаємо
, отримаємо ![]() , тобто закон Дюлонга-Пті. При низьких температурах (Т<<
, тобто закон Дюлонга-Пті. При низьких температурах (Т<<![]() ), коли
), коли ![]() , отримаємо “закон кубів Дебая”
, отримаємо “закон кубів Дебая”
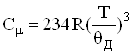 , (6.51)
, (6.51)
який кількісно узгоджується з експериментом (мал.6.9).
В рамках концепції корпускулярно-хвильового дуалізму речовини зміну енергії коливного руху кристалічної гратки можна описати процесами випромінювання чи поглинання особливої квазічастинки – фонона, яка володіє нульовим спіном і тому належить до класу бозонів (§6.7) .
§ 6.9. Елементи зонної теорії твердих тіл
При утворенні кристалічної гратки твердих тіл, тобто при зближенні окремих атомів на відстані ![]() , атомні енергетичні рівні повинні розщеплюватись в зони рівнів, оскільки принцип Паулі тепер стосується не окремих атомів, а кристалічної гратки в цілому. Розщеплення тим сильніше, чим менша відстань між атомами і чим вищий енергетичний рівень (мал.6.10). Таким чином шкала енергій електронів в кристалічній гратці розбивається на зони дозволених енергій і зони заборонених енергій (на мал.6.10б заштриховані зони дозволених енергій, які відповідають рівноважній відстані між атомами R0).
, атомні енергетичні рівні повинні розщеплюватись в зони рівнів, оскільки принцип Паулі тепер стосується не окремих атомів, а кристалічної гратки в цілому. Розщеплення тим сильніше, чим менша відстань між атомами і чим вищий енергетичний рівень (мал.6.10). Таким чином шкала енергій електронів в кристалічній гратці розбивається на зони дозволених енергій і зони заборонених енергій (на мал.6.10б заштриховані зони дозволених енергій, які відповідають рівноважній відстані між атомами R0).
Кількість енергетичних рівнів в зонах співмірна з кількістю атомів речовини, тобто ![]() . Оскільки ширина зон
. Оскільки ширина зон ![]() , то відстань між окремими рівнями
, то відстань між окремими рівнями ![]() , що значно менше від енергії теплового руху к0Т. І тому можна вважати розподіл енергій в зонах неперервним.
, що значно менше від енергії теплового руху к0Т. І тому можна вважати розподіл енергій в зонах неперервним.
У відповідності з принципом Паулі на кожному енергетичному рівні в зонах може перебувати не більше двох електронів з протилежними спінами. Якщо зона утворена з повністю заповненого електронами атомного рівня, то всі рівні такої зони також повністю заповнені. Зрозуміло, що це стосується зон, утворених з глибоких атомних рівнів. Електрони таких зон не можуть брати участь в електричних і теплових явищах, бо ні енергія електричного поля, ні теплова енергія не є достатніми для переводу електрона в сусідню вищу зону, а переходи в межах заповненої зони неможливі.
Інша ситуація в зонах, утворених з частково заповнених рівнів, тобто рівнів валентних електронів. Зрозуміло, що такі зони будуть заповнені також частково. Для прикладу розглянемо зону, утворену з атомного s-рівня, на якому перебуває лише один (валентний) електрон (Li, Na, K тощо). Якщо кристалічна гратка утворена з N атомів, то вказана зона має N рівнів, на яких може розміститись 2N електронів. Оскільки валентних електронів лише N, то заповниться лише половина зони (мал.6.11а ). А це означає, що під впливом зовнішнього збудження (тепло, електричне поле) електрони можуть вільно переходити на вищі рівні в межах однієї зони, тим самим збільшувати свою енергію, тобто прискорюватися. Отже, електрони в частково заповненій зоні є носіями струму. І тому така зона, яку ми назвемо валентною, є одночасно зоною провідності.
В залежності від характеру заповнення валентної зони всі тверді тіла поділяються на метали, з одного боку (мал.6.11а), і напівпро- відники та діелектрики, з іншого (мал.6.11б). В металах валентна зона (V-зона) заповнена частково, всі вищі зони порожні, всі нижчі зони заповнені повністю. В напівпровідниках і діелектриках V-зона заповнена повністю (при Т=0) і тому не може бути зоною провідності. Наступна вища зона при Т=0 повністю порожня. Ця зона називається зоною провідності (С-зоною), бо при певних умовах (Т![]() ) в ній можуть з’явитися електрони, які будуть носіями струму. Енергетична відстань між дном С-зони (Ес) і стелею V-зони (Еv) називається забороненою зоною Еg=Ec–Ev. Якщо Еg<2,5eB, то речовина – напівпровідник, якщо Еg>2,5eB, то – діелектрик.
) в ній можуть з’явитися електрони, які будуть носіями струму. Енергетична відстань між дном С-зони (Ес) і стелею V-зони (Еv) називається забороненою зоною Еg=Ec–Ev. Якщо Еg<2,5eB, то речовина – напівпровідник, якщо Еg>2,5eB, то – діелектрик.
Появу носіїв струму в напівпровідниках пояснимо, використавши плоску модель кристалічної гратки атомного напівпровідника, наприклад, Ge (мал.6.12). Такий напівпро- відник має тетраедричну криста- лічну структуру, при якій кожен атом оточений чотирма сусідами. Зв’язок між сусідніми атомами забезпечується двома валентними електронами з протилежними спінами. При Т=0 всі валентні електрони перебувають на зв’язках, “зайвих” електронів немає, що відповідає повністю заповненій валентній зоні і порожній зоні провідності.
При нагріванні кристалу деякі електрони за рахунок енергії теплового руху можуть вийти із зв’язків, стати вільними і в електричному полі напруженістю ![]() набути швидкості напрямленого руху
набути швидкості напрямленого руху ![]() . На звільнене вакантне місце може перейти електрон із сусіднього зв’язку, що рівнозначне рухові дірки (hole) в протилежному напрямку зі швидкістію
. На звільнене вакантне місце може перейти електрон із сусіднього зв’язку, що рівнозначне рухові дірки (hole) в протилежному напрямку зі швидкістію ![]() . Оскільки дірка рухається за полем (електрон – проти поля), то дірку слід розглядати як позитивний заряд +е. На енергетичній діаграмі теплова генерація вільних електронів і дірок зображається як перехід електрона з V-зони у C-зону (мал.6.13). Зрозуміло, що чим вища інтенсивність теплового збудження (чим вища температура), тим вища концентрація електронів (n) і дірок (р) у відповідних зонах. Відмітимо, що ця концентрація не перевищує, як правило, 0,1% від кількості енергетичних рівнів в зонах. Отже, електрони є носіями струму в майже порожній зоні провідності, а дірки – в майже повністю заповненій валентній зоні.
. Оскільки дірка рухається за полем (електрон – проти поля), то дірку слід розглядати як позитивний заряд +е. На енергетичній діаграмі теплова генерація вільних електронів і дірок зображається як перехід електрона з V-зони у C-зону (мал.6.13). Зрозуміло, що чим вища інтенсивність теплового збудження (чим вища температура), тим вища концентрація електронів (n) і дірок (р) у відповідних зонах. Відмітимо, що ця концентрація не перевищує, як правило, 0,1% від кількості енергетичних рівнів в зонах. Отже, електрони є носіями струму в майже порожній зоні провідності, а дірки – в майже повністю заповненій валентній зоні.
Енергія вільного електрона
 , (6.52)
, (6.52)
де р – імпульс електрона. В багатьох випадках для опису енергії електронів в металах і напівпровідниках можна користуватись цією ж формулою, але ввівши замість маси спокою електрона m0 ефективну масу mn*, яка може бути як більшою, так і меншою m0, і яка враховує взаємодію зонних електронів з полем кристалічної гратки. Аналогічно вводиться і ефективна маса зонних дірок mp*. І тому енергії електронів і дірок виражаються через їх імпульси наступним чином
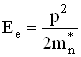 ;
; 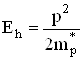 , (6.53)
, (6.53)
де відлік енергії ведеться від краю відповідної зони: вверх від Ес для електронів і вниз від Еv для дірок. Співвідношення (6.53) називаються законами дисперсії.
§ 6.10. Розподіл і концентрація носіїв в зонах
Розподіл частинок з напівцілим спіном (ферміонів), в т.ч. і електронів, за енергіями описується квантовою функцією розподілу Фермі-Дірака
f(E)= , (6.54)
, (6.54)
де f(E) – імовірність електрону перебувати на рівні з енергією Е, а F – енергія (рівень) Фермі. Зміст останньої зрозумілий з аналізу f(F) при Т=0. Якщо Е>F, то f(Е)=0, тобто рівень порожній; якщо Е<F, то f(F)=1, тобто рівень заповнений. Отже, енергія Фермі відповідає найвищому рівню, який ще заповнений при Т=0 (мал.6.14). При Т>0 f(F)=1/2, якщо Е=F, тобто енергія Фермі відповідає рівню, який при ненульовій температурі заповнений наполовину (мал.6.14). При певних умовах, а саме, коли Е-F>>к0Т, квантовий розподіл Фермі-Дірака переходить в класичний розподіл Максвелла-Больцмана
f(Е)=A(T)![]() .
.![]() (6.55)
(6.55)
Електронний газ, що описується таким розподілом, називається невиродженим газом. В цей же час електронний газ, що описується розподілом Фермі-Дірака, називається виродженим. Критерієм виродження є нерівність
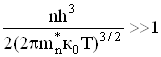 , (6.56)
, (6.56)
тобто виродження має місце при високій концентрації електронів, малій їх ефективній масі та низьких температурах. В металах електронний газ завжди вироджений (n![]() , в напівпровідниках, як правило, невироджений (n<
, в напівпровідниках, як правило, невироджений (n<![]() .
.
В металах при низьких температурах концентрація електронів зони провідності, енергія яких лежить в інтервалі ![]() ,
,
dn(E)=2dg(E),
де dg(E) – кількість енергетичних рівнів у вказаному інтервалі. Якщо справедливий параболічний закон дисперсії (6.53), то нескладний розрахунок дає
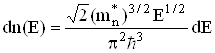 .
.![]() (6.57)
(6.57)
Тоді повна концентрація носіів в с-зоні металу при низьких температурах
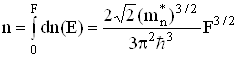 (6.58)
(6.58)
і від температури не залежить. Енергія Фермі
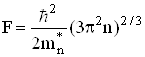 , (6.59)
, (6.59)
що дає ![]() при
при ![]() . Середня енергія зонних електронів в металах
. Середня енергія зонних електронів в металах 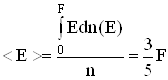 , що значно більше к0Т.
, що значно більше к0Т.
А це означає, що лише незначна кількість електронів, що перебувають на рівнях, близьких до рівня Фермі, може змінити свою енергію при зміні температури. Таким чином, електронний газ в металах практично не вносить вкладу в теплоємність кристалу (див. § 6.8), незважаючи на високу загальну концентрацію електронів.
В напівпровідниках рівень Фермі, як правило, лежить в забороненій зоні (мал.6.13), і тому при розрахунку концентрації невироджених електронів в зоні провідності потрібно врахувати, що функція розподілу (6.55) в усьому діапазоні енергій Е>Ec менша від одиниці і залежить від температури. І тому
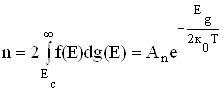 , (6.60)
, (6.60)
де Аn – множник, який слабо залежить від температури і визначається ефективною масою носіїв, а Еg – ширина забороненої зони.
Як слідує з (6.60) з ростом температури концентрація зонних (вільних) електронів збільшується за експоненційним законом. Ця формула справедлива лише для бездомішкового, т.з. власного, напівпровідника. Зрозуміло (див. мал. 6.13), що концентрація дірок у валентній зоні дорівнює концентрації електронів в зоні провідності: n=p=ni – власна концентрація носіїв струму.
Ситуація радикально змінюється, коли в напівпровідник ввести домішки. Зокрема, коли вводяться донорні домішки, тобто домішки, які легко віддають електрони в С-зону, то n>>p; такий домішковий напівпровідник називається електронним (n-типу). Якщо ж вводяться акцепторні домішки, тобто домішки, які легко захоплюють електрони з V-зони, то p>>n; такий домішковий напівпровідник називається дірковим (р-типу). В класичних напівпровідниках Ge i Si в ролі донорних домішок виступають As, P, а акцепторних – Ga, Іn.
§ 6.11. Електричні властивості металів і напівпровідників
Відомо (розділ ІІІ), що густина електричного струму в провідниках (металах, напівпровідниках, електролітах тощо) визначається зарядом носіїв, їх концентрацією n та середньою швидкістю напрямленого (впорядкованого) руху <![]() , зумовленого електричним полем напруженістю
, зумовленого електричним полем напруженістю ![]() . Якщо носіями струму є електрони, то густина струму (j=
. Якщо носіями струму є електрони, то густина струму (j=![]()
j=en<un> . (6.61)
В слабких електричних полях, де виконується закон Ома, швидкість напрямленого руху лінійно залежить від напруженості електричного поля, тобто
![]() , (6.62)
, (6.62)
де ![]() – рухливість електронів.
– рухливість електронів.
Підставляючи (6.62) в (6.61), отримаємо
![]() , (6.63)
, (6.63)
тобто закон Ома в диференційній формі, де
![]() – (6.64)
– (6.64)
питома електропровідність електронного провідника (металу, напівпровідника n-типу).
Питома електропровідність власного напівпровідника
![]() , (6.65)
, (6.65)
де ![]() – рухливість дірок.
– рухливість дірок.
Рухливість носіїв визначається так званим часом релаксації ![]() , який формально можна розглядати як проміжок часу між двома послідовними актами зіткнення (розсіяння) носіїв з недосконалостями кристалу. Основними недосконалостями (відхиленнями від ідеальності) є коливання кристалічної гратки (фонони) і домішки кристалу. В рамках вказаного формалізму середній час релаксації носіїв
, який формально можна розглядати як проміжок часу між двома послідовними актами зіткнення (розсіяння) носіїв з недосконалостями кристалу. Основними недосконалостями (відхиленнями від ідеальності) є коливання кристалічної гратки (фонони) і домішки кристалу. В рамках вказаного формалізму середній час релаксації носіїв
![]() , (6.66)
, (6.66)
де ![]() – середня довжина вільного (між двома послідовними зіткненнями) пробігу носіїв, <
– середня довжина вільного (між двома послідовними зіткненнями) пробігу носіїв, <![]() > – середня швидкість теплового (хаотичного) руху носіїв.
> – середня швидкість теплового (хаотичного) руху носіїв.
Строга квантова теорія дає
![]() . (6.67)
. (6.67)
Підставляючи (6.67) у (6.64), отримаємо для питомої електропровідності металів
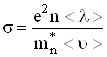 . (6.68)
. (6.68)
Оскільки в металах концентрація носіїв (електронів у С-зоні) від температури не залежить, то залежність питомої електропровідності визначається лише відношенням ![]() . Виявляється, що, за винятком дуже низьких температур,
. Виявляється, що, за винятком дуже низьких температур, ![]() . І тому
. І тому ![]() , а питомий опір
, а питомий опір ![]() , у відповідності з відомим експериментальним законом
, у відповідності з відомим експериментальним законом ![]() . Відмітимо, що при оціночних розрахунках можна покладати
. Відмітимо, що при оціночних розрахунках можна покладати ![]() .
.
Принципово інша ситуація в напівпровідниках, де концентрація носіїв експоненційно залежить від температури (6.60). Рухливість носіїв в напівпровідниках також залежить від температури, але за слабшим, степеневим законом:
![]() , (6.69)
, (6.69)
де ![]() при різних температурах приймає значення від –1,5 до +1,5. Підставляючи (6.60) та (6.69) у (6.65), отримаємо вираз для питомої електропровідності власного (n=p) напівпровідника
при різних температурах приймає значення від –1,5 до +1,5. Підставляючи (6.60) та (6.69) у (6.65), отримаємо вираз для питомої електропровідності власного (n=p) напівпровідника
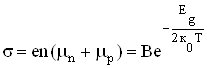 , (6.70)
, (6.70)
де передекспоненційний множник В можемо наближено вважати від температури незалежним. Узагальнюючи (6.70) на випадок домішкового напівпровідника, запишемо
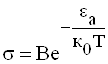 , (6.71)
, (6.71)
де ![]() а – енергія активації провідності, яка у власному напівпровіднику дорівнює
а – енергія активації провідності, яка у власному напівпровіднику дорівнює ![]() , а в домішкових напівпровідниках має зміст енергії іонізації донорів чи акцепторів. Отже, питома електропровідність напівпровідників експоненційно збільшується з ростом температури, чим останні принципово відрізняються від металів.
, а в домішкових напівпровідниках має зміст енергії іонізації донорів чи акцепторів. Отже, питома електропровідність напівпровідників експоненційно збільшується з ростом температури, чим останні принципово відрізняються від металів.
Розділ VII. Фізика ядра та елементарних часток.
§ 7.1. Склад і характеристики ядра
Ядро атома, як центральну позитивно заряджену масивну частину атома, навколо якої рухаються електрони, відкрив англійський фізик Е.Резерфорд на основі своїх дослідів по розсіюванню ![]() - частинок речовиною (1911 р). Позитивний заряд ядра чисельно рівний сумі негативних зарядів електронів нейтрального атома. За обрахунками Резерфорда радіус ядра rя~10-15м (радіус атома ra~10-10м). Плідність ядерної моделі атома підтвердила теорія атома водню Н.Бора (1913 р). Після того, як Г. Мозлі (1913 р) експериментально показав, що позитивний заряд ядра
- частинок речовиною (1911 р). Позитивний заряд ядра чисельно рівний сумі негативних зарядів електронів нейтрального атома. За обрахунками Резерфорда радіус ядра rя~10-15м (радіус атома ra~10-10м). Плідність ядерної моделі атома підтвердила теорія атома водню Н.Бора (1913 р). Після того, як Г. Мозлі (1913 р) експериментально показав, що позитивний заряд ядра
![]() , (7.1)
, (7.1)
де Z – порядковий номер елемента в таблиці Менделєєва, а е – елементарний електричний заряд, чисельно рівний зарядові електрона (![]() , уявлення про ядро атома стало загальноприйнятим.
, уявлення про ядро атома стало загальноприйнятим.
Ядра атомів різних хімічних елементів мають загальну назву нукліди. В ядерній фізиці за одиницю заряду приймають елементарний електричний заряд е, а за одиницю маси – атомну одиницю маси (а.о.м.). 1а.о.м. рівна 1/12 маси найбільш поширеного нукліда вуглецю. Очевидно, 1а.о.м.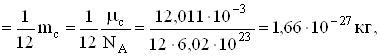
де mc – маса нукліда вуглецю, ![]() – маса моля вуглецю, NA – число Авогадро. В таких одиницях заряд ядра Q=Z (Z називають зарядовим числом ядра), а маси нуклідів різних елементів виражаються дробовими числами. Заокруглена до найближчого цілого маса нукліда даного елемента, виражена в а.о.м., співпадає з так званим масовим числом нукліда А.
– маса моля вуглецю, NA – число Авогадро. В таких одиницях заряд ядра Q=Z (Z називають зарядовим числом ядра), а маси нуклідів різних елементів виражаються дробовими числами. Заокруглена до найближчого цілого маса нукліда даного елемента, виражена в а.о.м., співпадає з так званим масовим числом нукліда А.
Зарядове число Z і масове число А являються основними характеристиками будь-якого ядра, тому ядро даного елемента позначається хімічним символом цього елемента з індексами Z та А, а саме – ![]() . Наприклад, ядро атома водню позначається
. Наприклад, ядро атома водню позначається ![]() ; цю частинку Резерфорд назвав протон (р). На момент відкриття ядра була вже відома легка негативно заряджена частинка електрон (
; цю частинку Резерфорд назвав протон (р). На момент відкриття ядра була вже відома легка негативно заряджена частинка електрон (![]() –). Оскільки маса електорна
–). Оскільки маса електорна ![]() , електрон, іноді, позначається
, електрон, іноді, позначається ![]() . При розгляді ядерних реакцій на основі законів збереження енергії та імпульсу Д.Чедвік (1932р.) відкрив нову важку елементарну частинку нейтрон (n). Д.Іваненко (1932р.) висунув гіпотезу, що ядро атома складається з нуклонів : протонів і нейтронів; ця гіпотеза була розвинута В. Гейзенбергом (1932 р) і дістала дослідне підтвердження.
. При розгляді ядерних реакцій на основі законів збереження енергії та імпульсу Д.Чедвік (1932р.) відкрив нову важку елементарну частинку нейтрон (n). Д.Іваненко (1932р.) висунув гіпотезу, що ядро атома складається з нуклонів : протонів і нейтронів; ця гіпотеза була розвинута В. Гейзенбергом (1932 р) і дістала дослідне підтвердження.
Детальне вивчення нуклонів показало, що протон – стабільна елементарна частинка з зарядом +1 і масою mp=1,00728 а.о.м.; він також має спін j=1/2 і магнітний момент ![]() , де
, де ![]() Дж/Тл – так званий ядерний магнетон (одиниця магнітного моменту). Нейтрон – нейтральна частинка з масою mn=1,00867 а.о.м., спіном j=1/2 і власним магнітним моментом
Дж/Тл – так званий ядерний магнетон (одиниця магнітного моменту). Нейтрон – нейтральна частинка з масою mn=1,00867 а.о.м., спіном j=1/2 і власним магнітним моментом ![]() ; mn>mp , при чому mn–mp=2,5me. У вільному стані нейтрон – нестабільний з періодом напіврозпаду Т~12 хв.
; mn>mp , при чому mn–mp=2,5me. У вільному стані нейтрон – нестабільний з періодом напіврозпаду Т~12 хв.
Згідно з нуклонною моделлю ядро ![]() містить всього А нуклонів; власне, під масовим числом ядра і розуміють загальне число нуклонів (протонів і нейтронів) у ядрі. При цьому, число протонів у ядрі є Z, а число нейтронів – N=A–Z. Ядра з однаковими Z називаються ізотопами, з однаковими А – ізобарами, з однаковими N – ізотонами, з однаковими Z i A, але різними періодами напіврозпаду,– ізомерами. Всього відомо ~ 1500 різних ядер, які чим-небудь відрізняються; приблизно 1/5 з них – стабільні, решта – радіоактивні.
містить всього А нуклонів; власне, під масовим числом ядра і розуміють загальне число нуклонів (протонів і нейтронів) у ядрі. При цьому, число протонів у ядрі є Z, а число нейтронів – N=A–Z. Ядра з однаковими Z називаються ізотопами, з однаковими А – ізобарами, з однаковими N – ізотонами, з однаковими Z i A, але різними періодами напіврозпаду,– ізомерами. Всього відомо ~ 1500 різних ядер, які чим-небудь відрізняються; приблизно 1/5 з них – стабільні, решта – радіоактивні.
В природі зустрічаються елементи з атомним номером Z від 1 до 92 (крім технецію ![]() і прометію
і прометію ![]() ). Трансуранові елементи, починаючи з Z=93, були одержані штучно за допомогою різних ядерних реакцій. Згідно з сучасними уявленнями хімічні елементи виникли в процесі нуклеосинтезу на етапі зоряної еволюції Всесвіту. За час існування Землі (~5
). Трансуранові елементи, починаючи з Z=93, були одержані штучно за допомогою різних ядерних реакцій. Згідно з сучасними уявленнями хімічні елементи виникли в процесі нуклеосинтезу на етапі зоряної еволюції Всесвіту. За час існування Землі (~5![]() трансуранові елементи із-за відносно малого часу життя не збереглися в земній корі (за винятком
трансуранові елементи із-за відносно малого часу життя не збереглися в земній корі (за винятком ![]() і
і ![]() , мікросліди яких знайдені в уранових рудах). Межу періодичної системи елементів повинна визначати нестабільність відносно самовільного ділення ядер; є теоритичні вказівки, що ця межа може знаходитися поблизу Z=114 (можливо, Z=126).
, мікросліди яких знайдені в уранових рудах). Межу періодичної системи елементів повинна визначати нестабільність відносно самовільного ділення ядер; є теоритичні вказівки, що ця межа може знаходитися поблизу Z=114 (можливо, Z=126).
Ефективний радіус ядра виражається формулою
![]() , (7.2)
, (7.2)
де ![]() . З (7.2) випливає, що об’єм ядра пропорційний числу нуклонів у ядрі, а це означає, що густина ядерної речовини приблизно однакова для всіх ядер (~1017кг/м3).
. З (7.2) випливає, що об’єм ядра пропорційний числу нуклонів у ядрі, а це означає, що густина ядерної речовини приблизно однакова для всіх ядер (~1017кг/м3).
Спіни і магнітні моменти нуклонів складаються в результуючий спін і магнітний момент ядра. Оскільки спін нуклона ![]() , квантове число спіну ядра буде напівцілим при непарному числі нуклонів і – цілим або нулем при парному А. Спіни ядер не перевищують декількох одиниць, це свідчить, що спіни більшості нуклонів у ядрі компенсуються, розміщуючись антипаралельно.
, квантове число спіну ядра буде напівцілим при непарному числі нуклонів і – цілим або нулем при парному А. Спіни ядер не перевищують декількох одиниць, це свідчить, що спіни більшості нуклонів у ядрі компенсуються, розміщуючись антипаралельно.
Взаємодією магнітних моментів ядра та електронів атома обумовлюється так звана надтонка структура атомних спектрів. Пов’язаний зі спіном ядра магнітний момент знайшов широкі застосування в експериментальній методиці ядерного магнітного резонансу.
§ 7.2. Дефект маси та енергія зв’язку ядра. Ядерні сили. Моделі ядра
Користуючись таблицею мас ізотопів, можна пересвідчитись, що маса ядра mя менша суми мас нуклонів, з яких воно складається. Величину
![]() (7.3)
(7.3)
називають дефектом маси ядра. Його існування обумовлене тим, що при об’єднанні нуклонів у ядро виділяється енергія у виді квантів, які виносять частину маси. Цю енергію можна розрахувати за формулою Ейнштейна про взаємозв’язок маси-енергії
![]() с2, (7.4)
с2, (7.4)
де с – швидкість світла у вакуумі. Очевидно, щоб розкласти ядро на невзаємодіючі нуклони, потрібно таку ж енергію затратити. Ця енергія
![]() (7.5)
(7.5)
називається енергією зв’язку ядра.
Для практичних застосувань співвідношення (7.5) зручно записувати у вигляді:
![]() с2, (7.6)
с2, (7.6)
де mн – маса атома водню, ma – маса атома елемента, ядро якого розглядається. При переході до наближеної формули (7.6) нехтують малою енергією зв’язку електронів з ядром; зручність (7.6) полягає у тому, що в довідниках наводяться не маси ядер mя, а маси атомів ізотопів ma. На основі (7.4) можна пересвідчитись, що 1а.о.м. еквівалентна енергії 931,5 МеВ, тому, виражаючи квадратну дужку формули (7.6) в а.о.м., для енергії зв’язку ядра в МеВ одержують:
![]() . (7.7)
. (7.7)
Очевидно, енергія зв’язку характеризує міцність ядра. Прийнято розглядати так звану питому енергію зв’язку ![]() (енергія зв’язку, що припадає на один нуклон). Розрахунки показують, що вона залежить від масового числа елемента (мал.7.1).
(енергія зв’язку, що припадає на один нуклон). Розрахунки показують, що вона залежить від масового числа елемента (мал.7.1).
Для легких ядер (![]()
![]() стрибкоподібно зростає до (6–7) МеВ, далі більш повільно зростає до максимального значення 8,7 МеВ у елементів з масовим числом
стрибкоподібно зростає до (6–7) МеВ, далі більш повільно зростає до максимального значення 8,7 МеВ у елементів з масовим числом
А~50–60, а тоді повільно зменшується у важких елементів (наприклад, для ![]()
![]() З (мал.7.1) видно, що найбільш стійкими є ядра середньої частини таблиці Менделєєва. Стає зрозумілим також, що енергетично можливими є два процеси, які повинні супроводжуватися виділенням енергії: 1) поділ важких ядер на більш легкі; 2) злиття (синтез) легких ядер у більш важкі. Обидва ці процеси реалізовані на Землі: перший – в ланцюговій реакції ділення важких ядер (атомна бомба, реактори), другий – в термоядерній реакції синтезу легких ядер (воднева бомба).
З (мал.7.1) видно, що найбільш стійкими є ядра середньої частини таблиці Менделєєва. Стає зрозумілим також, що енергетично можливими є два процеси, які повинні супроводжуватися виділенням енергії: 1) поділ важких ядер на більш легкі; 2) злиття (синтез) легких ядер у більш важкі. Обидва ці процеси реалізовані на Землі: перший – в ланцюговій реакції ділення важких ядер (атомна бомба, реактори), другий – в термоядерній реакції синтезу легких ядер (воднева бомба).
Величезна питома енергія зв’язку свідчить, що між нуклонами в ядрі діють особливі сили притягання, які значно переважають електромагнітну та гравітаційну взаємодію нуклонів. Взаємодія між нуклонами в ядрі одержала назву сильної взаємодії. Ядерні сили мають ряд характерних особливостей, вони:
1 – короткодіючі, радіус їх дії~10–15м;
2 – зарядовонезалежні, мають неелектричну природу;
3 – спіновозалежні, залежать від орієнтації спінів нуклонів;
4 є нецентральними, не напрямлені вздовж прямої, що з’єднує центри нуклонів;
5 мають властивість насичення, діють лише між найближчими сусідами.
У 1934 р. І.Є. Тамм висунув гіпотезу, що сильна взаємодія повинна мати обмінну природу. По аналогії з електромагнітною взаємодією, яка квантовою електродинамікою описується як процес віртуального обміну електронів фотонами:
![]() , (7.8)
, (7.8)
нуклони в ядрі повинні обмінюватись деякими віртуальними частинками з масою спокою відмінною від нуля. Віртуальними називаються частинки, час життя яких менший того, що визначається співвідношенням невизначеностей
![]() , (7.9)
, (7.9)
де ![]() – невизначеність енергії квантового стану,
– невизначеність енергії квантового стану, ![]() – тривалість існування цього стану,
– тривалість існування цього стану, ![]() – стала Дірака. З (7.9) випливає, що радіус дії обмінних сил оцінюється величиною
– стала Дірака. З (7.9) випливає, що радіус дії обмінних сил оцінюється величиною
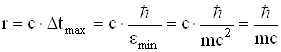 , (7.10)
, (7.10)
тобто він може бути скінченним, якщо маса спокою віртуальної частинки відмінна від нуля.
У 1935 р. Х. Юкава показав, що для пояснення величини ядерних сил слід припустити існування віртуальних частинок з масою спокою у 200–300 разів більшою маси спокою електрона. Віртуальна частинка може стати реальною, якщо їй надати достатньої енергії. Такі частинки були відкриті Поуелом і Оккіаліні (1947 р.) в космічних променях; вони дістали
назву ![]() -мезонів. Існують
-мезонів. Існують ![]() –мезони. Заряд
–мезони. Заряд ![]() –мезонів рівний елементарному зарядові е. Їх маса
–мезонів рівний елементарному зарядові е. Їх маса ![]() 273 me, маса
273 me, маса ![]() , спін усіх
, спін усіх ![]() –мезонів j=0, всі вони – нестабільні; час життя
–мезонів j=0, всі вони – нестабільні; час життя ![]() =2,6
=2,6![]() ,
, ![]() . За рахунок процесів:
. За рахунок процесів:
![]() , (7.11)
, (7.11)
![]() , (7.12)
, (7.12)
![]() ,
, ![]() (7.13)
(7.13)
здійснюється обмін нуклонів віртуальними ![]() –мезонами в ядрі, що приводить до сильної взаємодії між нуклонами.
–мезонами в ядрі, що приводить до сильної взаємодії між нуклонами.
Обмін нуклонів віртуальними ![]() –мезонами підтверджується, зокрема, дослідами по розсіюванню нейтронів на протонах, в яких були виявлені процеси перетворення нейтронів в протони і навпаки при проходженні пучка нейтронів через водень. На основі процесів (7.11), (7.12) можна пояснити магнітні моменти протона і нейтрона. Згідно з (7.11), магнітний момент протона (більший одного магнетона) обумовлений орбітальним рухом
–мезонами підтверджується, зокрема, дослідами по розсіюванню нейтронів на протонах, в яких були виявлені процеси перетворення нейтронів в протони і навпаки при проходженні пучка нейтронів через водень. На основі процесів (7.11), (7.12) можна пояснити магнітні моменти протона і нейтрона. Згідно з (7.11), магнітний момент протона (більший одного магнетона) обумовлений орбітальним рухом ![]() +–мезона у віртуальному стані протона n+
+–мезона у віртуальному стані протона n+![]() +. Від’ємний магнітний момент нейтрона обумовлений орбітальним рухом
+. Від’ємний магнітний момент нейтрона обумовлений орбітальним рухом ![]() ––мезона, коли, згідно з (7.12), нейтрон частину часу проводить у віртуальному стані р+
––мезона, коли, згідно з (7.12), нейтрон частину часу проводить у віртуальному стані р+![]() –.
–.
Незважаючи на пояснення природи ядерних сил, послідовна кількісна теорія ядра не побудована, бо являє собою громіздку квантову задачу багатьох тіл (А нуклонів). Це спонукає йти по шляху створення моделей ядра, які, за рахунок введення певних параметрів, що підбираються в узгодженні з дослідом, дозволяють простими засобами описувати деяку сукупність властивостей ядра. Найбільш аргументованими з них є краплинна та оболонкова моделі ядра.
Краплинна модель ядра (Я.І. Френкель, Н. Бор, 1935–1939 р.), базуючись на властивості насичення ядерних сил і молекулярних сил в рідині, а також на малій стисливості рідини і ядерної речовини, уподібнює ядро зарядженій краплині рідини. Це дозволило вивести напівемпіричну формулу для енергії зв’язку ядра і, зокрема, пояснити процеси ділення важких ядер.
Оболонкова модель ядра (М. Гепперт-Мейєр, 1949–1950 р.) базується на уявленні, що нуклони рухаються незалежно в усередненому центральносиметричному полі. У зв’язку з цим виникають дискретні енергетичні рівні, які заповнюються нуклонами на основі принципу Паулі. Ці рівні групуються в оболонки, в кожній з яких може знаходитись певне число нуклонів. Повністю заповнена оболонка являється особливо стійким утворенням. Такими особливо стійкими (магічними) є ядра, у яких число протонів Z або число нейтронів N рівні 2, 8, 20, 28, 50, 82, 126. Ядра, у яких магічними є Z та N, називаються двічі магічними. Їх відомо п’ять: ![]() ,
, ![]()
![]()
![]()
![]() вони – особливо стійкі. Зокрема, мабуть тому
вони – особливо стійкі. Зокрема, мабуть тому ![]() -частинка (
-частинка (![]() ) – єдина складна частинка, яка випромінюється важкими ядрами при радіоактивності.
) – єдина складна частинка, яка випромінюється важкими ядрами при радіоактивності.
§ 7.3. Радіоактивність
Радіоактивність – процес самовільного перетворення нестабільних ядер в інші з випромінюванням часток. До радіоактивних перетворень відносяться: ![]() -розпад,
-розпад, ![]() -розпад (з випромінюванням електрона, позитрона чи захопленням орбітального електрона), самовільне ділення ядер, протонна та нейтронна радіоактивність, інші види розпадів. Радіоактивність нестабільних ядер, які існують в природніх умовах, називається природньою (А.Беккерель, 1896 р.), а тих, що одержані шляхом ядерних реакцій,– штучною (І. та Ф. Жоліо-Кюрі,1934 р). Обидва види радіоактивності підкоряються одному законові радіоактивного розпаду.
-розпад (з випромінюванням електрона, позитрона чи захопленням орбітального електрона), самовільне ділення ядер, протонна та нейтронна радіоактивність, інші види розпадів. Радіоактивність нестабільних ядер, які існують в природніх умовах, називається природньою (А.Беккерель, 1896 р.), а тих, що одержані шляхом ядерних реакцій,– штучною (І. та Ф. Жоліо-Кюрі,1934 р). Обидва види радіоактивності підкоряються одному законові радіоактивного розпаду.
Із-за незалежності радіоактивних перетворень окремих ядер можна вважати, що число ядер dN, які розпадаються за проміжок часу dt, пропорційне наявному числу ядер N і величині проміжку dt:
![]() , (7.14)
, (7.14)
де ![]() – постійна розпаду,яка характеризує ймовірність розпаду ядра за одиницю часу; знак мінус вказує, що число ядер зменшується з часом. Інтегруючи (7.14) при умові
– постійна розпаду,яка характеризує ймовірність розпаду ядра за одиницю часу; знак мінус вказує, що число ядер зменшується з часом. Інтегруючи (7.14) при умові ![]() , одержуємо
, одержуємо
![]() . (7.15)
. (7.15)
Закон радіоактивного розпаду (7.15) показує, що число радіоактивних ядер N, які не розпалися до моменту часу t, зменшується з часом експоненційно (мал.7.2).
Кількість ядер, які розпались за час t,
![]() , (7.16)
, (7.16)
Час Т, протягом якого розпадається половина початкової кількості ядер, називається періодом напіврозпаду. З (7.16) при t=T i ![]() випливає
випливає
![]() . (7.17)
. (7.17)
Період напіврозпаду відомих радіонуклідів змінюється в дуже широких межах: від ![]() с до
с до ![]() років. Очевидно, величина
років. Очевидно, величина ![]() характеризує середній час життя ядра, тому з (7.14) випливає
характеризує середній час життя ядра, тому з (7.14) випливає
![]() . (7.18)
. (7.18)
Виявляється, що в процесі радіоактивного перетворення материнського ядра виникає дочірнє ядро, яке теж може бути радіоактивним, і т.д. Тому виникає ряд радіоактивних елементів, генетично зв’язаних між собою. Для природньорадіоактивних елементів відомо 3 таких ряди: ряд торію ![]() ряд урану
ряд урану ![]() ряд актинію
ряд актинію ![]() які закінчуються стабільними ізотопами свинцю
які закінчуються стабільними ізотопами свинцю ![]()
![]()
![]() З часом в кожному радіоактивному ряді встановлюється так звана вікова рівновага, при якій швидкості утворення і розпаду проміжних членів ряду рівні, що дає
З часом в кожному радіоактивному ряді встановлюється так звана вікова рівновага, при якій швидкості утворення і розпаду проміжних членів ряду рівні, що дає
![]() . (7.19)
. (7.19)
Вікова рівновага встановлюється на протязі проміжку часу ![]() найбільш довгоживучого члена ряду. По мірі його розпаду загальний вміст членів ряду в земній корі повільно зменшується. Наприклад, для
найбільш довгоживучого члена ряду. По мірі його розпаду загальний вміст членів ряду в земній корі повільно зменшується. Наприклад, для ![]() через великі проміжки часу виникає стільки ядер свинцю, скільки розпадається ядер урану. Тому, вимірюючи концентрацію урану і свинцю в уранових рудах, можна оцінити середній вік Землі, що дає величину ~4,5
через великі проміжки часу виникає стільки ядер свинцю, скільки розпадається ядер урану. Тому, вимірюючи концентрацію урану і свинцю в уранових рудах, можна оцінити середній вік Землі, що дає величину ~4,5![]() років.
років.
Вже перші дослідники природньої радіоактивності (П. та М. Кюрі, Е.Резерфорд) виявили, що радіоактивна речовина є джерелом трьох видів випромінювань: ![]() -,
-, ![]() - і
- і ![]() -променів.
-променів. ![]() -промені являють собою потік ядер гелію
-промені являють собою потік ядер гелію ![]() .
. ![]() -розпад відбувається за схемою
-розпад відбувається за схемою
![]() . (7.20)
. (7.20)
Індекси дочірнього ядра встановлюються на основі законів збереження зарядового і масового чисел: зарядове чи масове число до реакції рівне сумі відповідних чисел після реакції. Звідси випливають так звані правила зміщення; зокрема, при ![]() -розпаді Z дочірнього ядра на 2, а А на 4 менше, ніж у материнського ядра, наприклад
-розпаді Z дочірнього ядра на 2, а А на 4 менше, ніж у материнського ядра, наприклад
![]() .
.
Енергія реакції ![]() -розпаду визначається на основі формули (7.7), де дефект маси реакції
-розпаду визначається на основі формули (7.7), де дефект маси реакції
![]() . (7.21)
. (7.21)
Ця енергія виділяється у вигляді кінетичної енергії продуктів реакції, яку можна розрахувати на основі законів збереження енергії та імпульсу.
У більшості випадків радіоактивний елемент випромінює ![]() -частинки декількох чітко визначених груп. Це обумовлено тим, що дочірнє ядро може виникати не тільки в основному стані 1, але і в збуджених станах 2,3,… (мал.7.3). За час існування збуджених станів
-частинки декількох чітко визначених груп. Це обумовлено тим, що дочірнє ядро може виникати не тільки в основному стані 1, але і в збуджених станах 2,3,… (мал.7.3). За час існування збуджених станів ![]() с дочірнє ядро переходить в більш низький чи нормальний стан, випромінюючи
с дочірнє ядро переходить в більш низький чи нормальний стан, випромінюючи ![]() -квант. Так виникають
-квант. Так виникають ![]() -промені, які, звичайно, супроводжують
-промені, які, звичайно, супроводжують ![]() -розпад, хоча дочірнє ядро може звільнитись від надлишку енергії також іншими способами: випромінюючи яку-небудь частинку, або йонізуючи атом (процес внутрішньої конверсії).
-розпад, хоча дочірнє ядро може звільнитись від надлишку енергії також іншими способами: випромінюючи яку-небудь частинку, або йонізуючи атом (процес внутрішньої конверсії).
Процес ![]() -розпаду не можна пояснити на основі класичної механіки: з радіоактивних ядер випромінюються
-розпаду не можна пояснити на основі класичної механіки: з радіоактивних ядер випромінюються ![]() -частинки з енергією ~6МеВ, в той же час, при бомбардуванні ядер
-частинки з енергією ~6МеВ, в той же час, при бомбардуванні ядер ![]() -частинками з енергією ~8МеВ такі
-частинками з енергією ~8МеВ такі ![]() -частинки не проникають в ядро. Ядро для
-частинки не проникають в ядро. Ядро для ![]() -частинки є потенціальним бар’єром, висота якого U0 більша енергії
-частинки є потенціальним бар’єром, висота якого U0 більша енергії ![]() -частинки Е (мал.7.4). Внутрішня сторона бар’єру обумовлена ядерними силами, зовнішня – силами кулонівського відштовхування. Явище стає зрозумілим на основі квантової механіки:
-частинки Е (мал.7.4). Внутрішня сторона бар’єру обумовлена ядерними силами, зовнішня – силами кулонівського відштовхування. Явище стає зрозумілим на основі квантової механіки: ![]() -частинка виникає в момент радіоактивного розпаду ядра і долає бар’єр ядра на основі тунельного ефекту (для мікро- частинки існує відмінна від нуля ймовірність проникнути через бар’єр з енергією, меншою висоти бар’єру; Г. Гамов, 1929 р).
-частинка виникає в момент радіоактивного розпаду ядра і долає бар’єр ядра на основі тунельного ефекту (для мікро- частинки існує відмінна від нуля ймовірність проникнути через бар’єр з енергією, меншою висоти бар’єру; Г. Гамов, 1929 р).
Маючи великий заряд і масу, ![]() -частинки інтенсивно йонізу- ють молекули речовини, тому пробіг
-частинки інтенсивно йонізу- ють молекули речовини, тому пробіг ![]() -частинок в речовині – незначний; вони, наприклад, повністю затримуються аркушем паперу. Проникна здатність
-частинок в речовині – незначний; вони, наприклад, повністю затримуються аркушем паперу. Проникна здатність ![]() - променів – значна: щоб зменшити їх інтенсивність вдвічі, потрібний шар свинцю товщиною~1см.
- променів – значна: щоб зменшити їх інтенсивність вдвічі, потрібний шар свинцю товщиною~1см.
Існує три різновиди ![]() -розпаду:
-розпаду: ![]() -розпад (ядро випромінює електрон
-розпад (ядро випромінює електрон ![]() ),
), ![]() -розпад (ядро випромінює позитрон
-розпад (ядро випромінює позитрон ![]() ) і так зване електронне захоплення (ядро поглинає один з електронів К–, рідше L–, чи М– шару свого атома).
) і так зване електронне захоплення (ядро поглинає один з електронів К–, рідше L–, чи М– шару свого атома).
![]() -розпад відбувається за схемою
-розпад відбувається за схемою
![]() ; (7.22)
; (7.22)
звідси видно, що при ![]() -розпаді масове число дочірнього ядра не змінюється, а зарядове число змінюється на одиницю, наприклад,
-розпаді масове число дочірнього ядра не змінюється, а зарядове число змінюється на одиницю, наприклад, ![]() . Пояснення
. Пояснення ![]() -розпаду зустрілося з труднощами:
-розпаду зустрілося з труднощами:
Похожие работы
... параметрів при термоциклюванні, а саме ця особливість є принциповою для практичного використання. Перспективними для вирішення проблеми деградації об’ємних матеріалів з ФПМН є склокерамічні матеріали на основі компонента з фазовим переходом метал-напівпровідник. Такі матеріали можна отримати за керамічною технологією. Важливою вимогою до них, окрім стабільної поведінки при термоциклюванні, є ...
... ій зоні. Для тіл, у яких ширина забороненої зони не перевищує 1 еВ, уже при кімнатній температурі в зоні провідності виявляється достатнє число електронів, а у валентній зоні – вакансій, щоб обумовити відносно високу електропровідність. Такі тіла звичайно називають напівпровідниками. Звідси стає ясним, що розподіл твердих тіл другої групи, на діелектрики й напівпровідників є чисто умовним. У ...
... заряджені дефекти впливають також на матричні елементи для переходів між нелокалізованими станами поблизу країв рухливості, створюючи флуктуації потенціалу. РОЗДІЛ 2 ФОТОІНДУКОВАНІ ЗМІНИ ОПТИЧНИХ ПАРАМЕТРІВ ТОНКИХ ШАРІВ НЕКРИСТАЛІЧНИХ ХАЛЬКОГЕНІДІВ 2.1. Структурні одиниці та фізико-хіміні особливості некристалічних халькогенідів Структура склоподібних і аморфних халькогенідів може бути ...
... Висновки. Одним з перспективних напрямків сучасної фізики є дослідження поверхні твердого тіла та взаємодії поверхневих електромагнітних хвиль інфрачервоного діапазону з поверхнею та тонкими шарами напівпровідників . При взаємодії світлової хвилі з поверхнею твердого тіла виникає поверхнева електромагнітна хвиля. Квазічастинки, які відповідають цим коливанням, що мають змішаний електромагнітно- ...
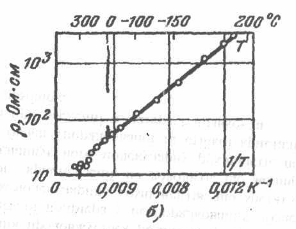
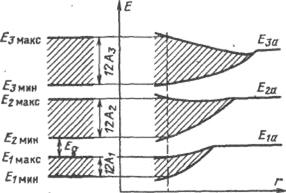
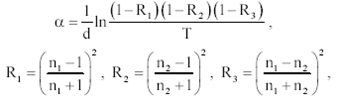
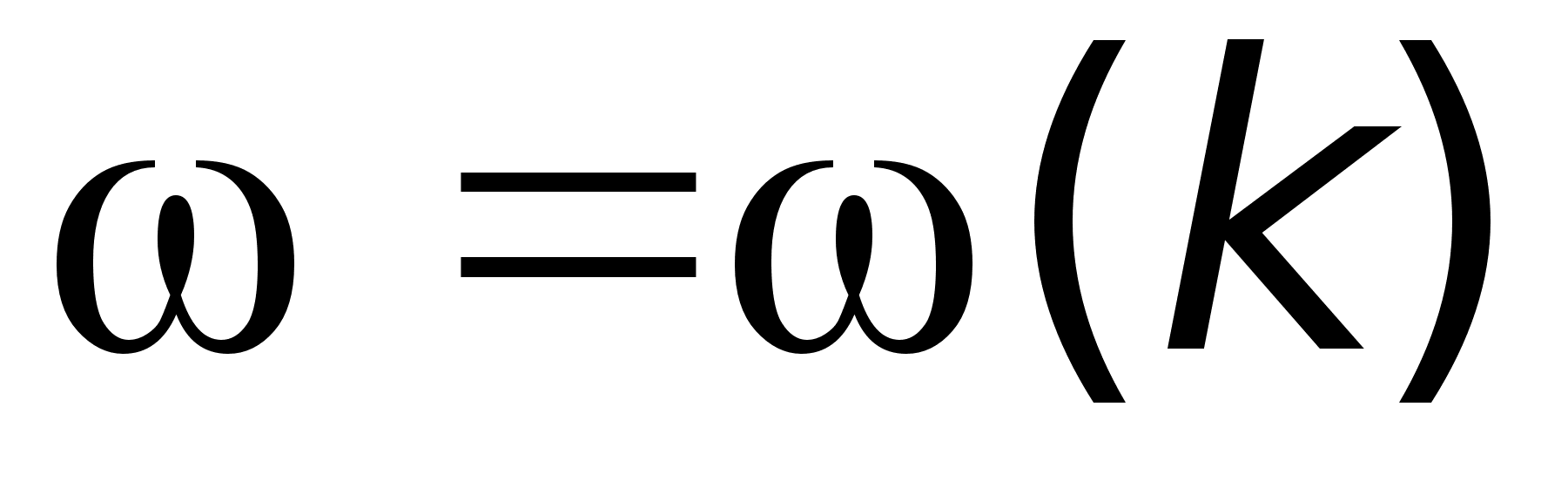
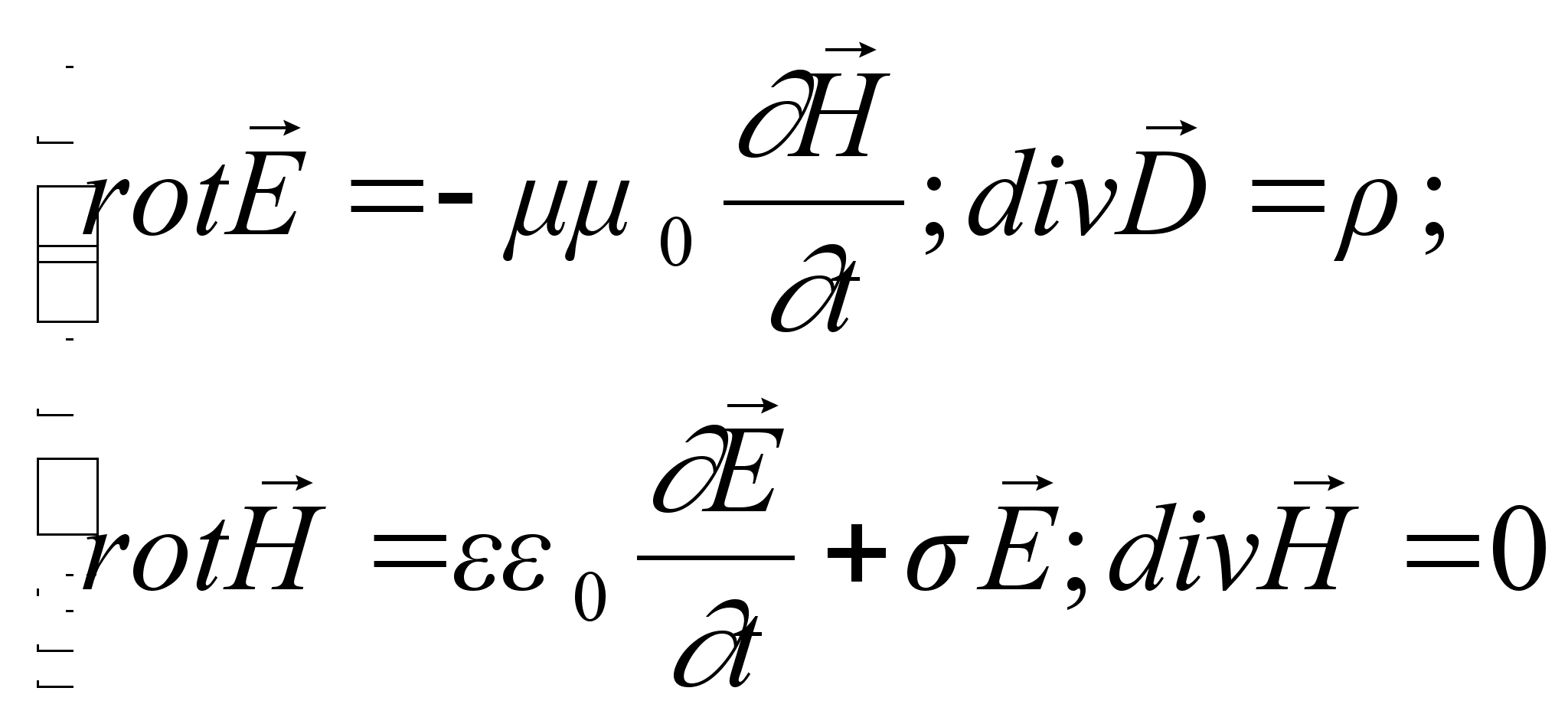
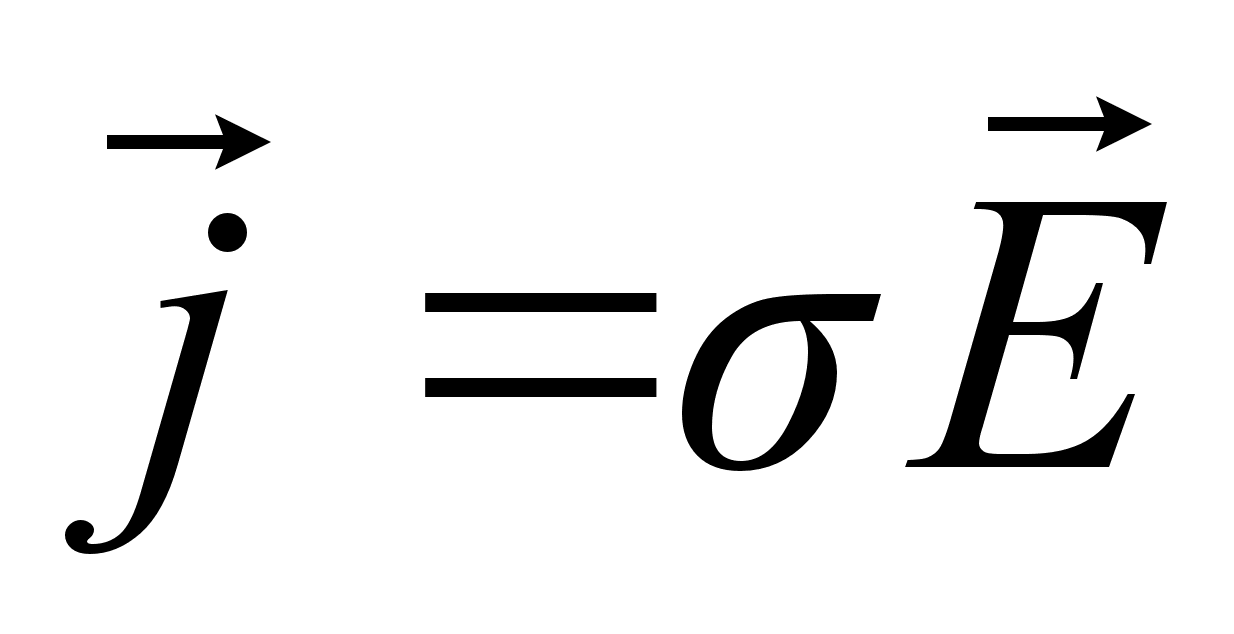
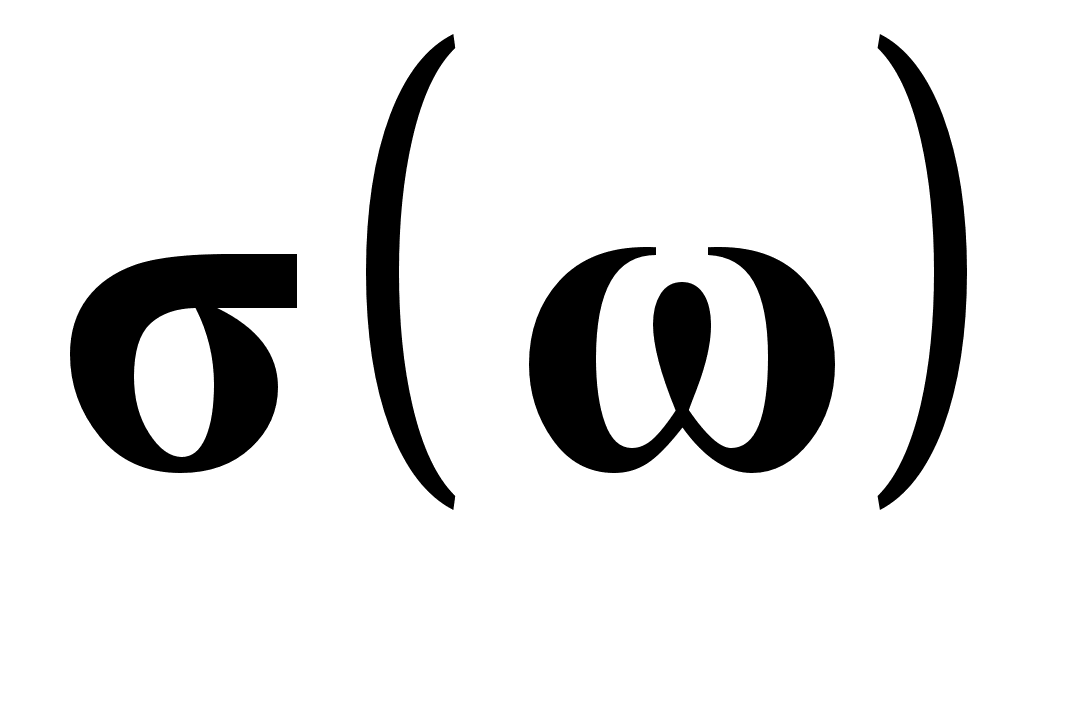
0 комментариев