£ t £ 2p

0 £ t £ 2p

Вопрос №6

Неприрывную кривую назыв. простой кривой (жордановой), если она не имеет точек самопересечения.

Областью называется всякое открытое связаное мн-во, т.е. такое мн-во всякая точка кот. явл. внутренней и любые две точки этого мн-ва можно соединить непрерывной кривой все точки кот. принадлежат данному мн-ву.

Область называется односвязной областью, если внутренность всякой замкнутой кривой содержит только точки данного мн-ва.

Теорема 1. Пусть Д ограниченная односвязная область пл-ти x и y, тогда для того чтобы криволинейный интеграл

был равен нулю по любой замкнутой кривой ГÌД, (где P(x,y) и Q(x,y) непрерыв. И имеет непрерыв. Частные производ.  и ) необходимо и достаточно чтобы вып. Такое равенство

= (2)

f(x,y)eД.

Док-во: Пусть во всей области Д вып. Равенство (2) и Г произвольная простая замкнутая кривая принадлеж. области Д. Обознач. Через обл. Д1 кот. огранич. Эта кривая Г. Применим к этой области формулу Грина:

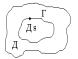
Предположим, что интеграл равен нулю, а равенство (2) не вып. По крайней мере в одной точке (x0 ,y0) e Д

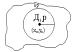
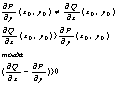
F(x0,y0)>0 , т.к. частные произв. Непрерывны в обл. Д, то ф-ция F(x,y) непрывна в этой обл. , а из этого вытекает , т.к. F(x0,y0)>0, то существует окрестность этой точки такая, что F(x,y)>0 для всех точек лежащих в нутри окр. gr кот. явл. Границей нашей окружности.

Множество точек леж. В этой окр. обознач. Д1 и применим к области Д1 ф-лу Грина:

это показывает, что не сущ. ни одной точки, где бы (2) не выполнялось. Вопрос №4

Пусть заданы 2 плоскости с введенными в прямоугольник декартовыми системами координат

 XOY и UOV. Пусть в плоскисти XOY задана область DV ограниченная кривой Г, а в плоскости UOV задана область G ограниченная кривой L

Пусть функция отображает область G в области D, где т.(u,v)e G, а т.(x,y)eD.

Будем предпологать , что функции x и y такие, что каждой точке области G соответствует точка области D и причем это соответствие такое, что различным точкам области D соответствуют различные области точки G. Причем всякая точка области D имеет единственный прообраз (u,v) в области G.

Тогда существует обратная функции  

 которая взаимноодназначно отображает область D в области G. Т.к. заданием двух точек U,V одназначно определяют т.(x,y) в области D, то числа U и V принято называть координатами точек в облати D, но уже криволинейными.

Будем предпологать, что функции x(U,V) и y(U,V) имеют непрерывные частные производные по своим переменным x’y и y’x, x’v и y’v, тогда определитель функции имеет вид:

Принято называть якобианом для функций x(U,V) и y(U,V).

Можно показать,что площадь области D задана в плоскости XOY может быть выражена в криволинейных координатах следующим образом:

 - прямолинейном интеграле.

в криволинейных координатах.

Замена переменных.

Теорема: Пусть Z=f(x) – непрерывная функция заданая в области D и область D является образом области G через посредства функций , где функции x(U,V) и y(U,V) непрерывные и имеют непрер. Частные производные, тогда справедлива след. Формула замены переменных в двойном интеграле:

Док-во: Разорвем обл.G непер. Кривыми на конечное число частичных областей. Тогда согласно формулам отображающим область G в обл. D. Эти кривые обл. G отображ. В некоторые кривые обл. D, т.е. обл. D будет разбита на конечное число (такое же как и обл. G) частичных подобластей.

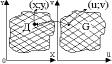
Di – подобласти, i=1,2,…,n.

В каждой обл. Di выберем т.(x,y)eDi и составим интегральную сумму Римана для двойного интеграла от функции f обл. D.

Площадь обл. Di выразим в криволинейных координатах

xi=x(Ui,Vi)

yi=y(Ui,Vi)

И того, что интеграл от функции f(x,y)dxdy сущ., то $ lim sn(f) и этот lim не зависит от выбора точек в обл. Di, но тогда в качестве f(xi,yi) может быть взята точка  

Мы получаем интегральную сумму Римана для интегр., что стоит справа формулы (1), поэтому переходя к lim в следующем равенстве:

 

получим ф-лу (1), т.к. суммы стремятся к соответствующему интегралу.Вопрос №2

Теорема: Пусть z = f(x,y) – ограниченная функция, заданная на прямоугольнике R = [a,b;c,d], и существует двойной интеграл по этому прямоугольнику

Если для " X [a,b] существует одномерный интеграл

то $ повторный интеграл

Доказательство:

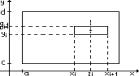
Разобьем отрезки ab и cd отрезками a=x0<x1<…<xn=b, c=y0<y1<…<yn=d. Рассмотрим теперь частичный прямоугольник Rik=[xi,xi+1;yi,yi+1] mik=inf f(x,y) Mik=sup f(x,y)

Rik Rik

На промежутке [xi;xi+1] возьмём точку x. Будем рас- сматривать точки, лежащие на прямой x = x.

Получаем следующее неравенство mik£ f(x;y)£ Mik yk£ y£ yk+1 Проинтегрируем его по отрезку [yk; yk+1]

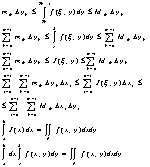
Замечание: если же существует двойной интеграл и существует одномерный интеграл

то существует повторный

Если же функция f(x;y) такова, что существует двойной интеграл по области R, существуют оба од- номерных J(y) и Ί(x), то одновременно имеют место формулы (1) и (2)

Например: если f(x;y) непрерывна в области R, то, как известно двойной интеграл, и оба одномерных существуют, а значит, справедлива формула (3) и для вычисления двойного интеграла можно пользоваться одной из формул (1) или (2), а именно выбирая ту или иную, которая даёт более простое решение.

7.Независемость криволинейного интегр. от пути интегрирования. Теор.1 и 2.

Теорема 1. Пусть D – ограниченная одно-связанная область плоскости XOY тогда что бы криволинейный интеграл -  был равен 0 по любой замкнутой простой кривой , где P(x,y) и Q(x,y) - непрерывны и имеют непрерывные частные производные , необходимо и достаточно что бы во всех точках области D было  (2).

Док-во

достаточность: Пусть во всех точках обл. D выполнено рав-во (2) и пусть Г произвольная простая замкнутая кривая, принадлежащая области. Обозначим через D область кот-ю ограничивает эта кривая Г. Применим теперь к этой области ф-лу Грина.

Необходимость: Криволинейный интеграл в любой замкнутой простой кривой существует область D=0. Покажем, что во всех точках области D выполняется рав-во (2). (это доказуется методом от противного). Пусть интеграл = нулю, а рав-во (2) не выполняется, по крайней мере, в одной точке , т.е. . Пусть,  так что разность . Пусть  тогда . Т.к. частные производные  и  непрерывны в области D, то  непрерывна в этой области, а из непрерывности функций вытекает что ф-ция , то существует окрестность этой точки, принадлежащая области D, так что везде в этой окрестности  для любой точки лежащей внутри кривой.

 кот-я является границей нашей окрестности  - множество чисел внутри . Применим к  ф-лу Грина: . Полученное противоречие показывает, что не существует не одной точки где бы равенство (2) не выполнялось.

Теорема 2 Пусть D есть односвязная область плоскости XOY в этой области заданы две непрерывные функции D(x,y) и Q(x,y) имеющие непрерывные частные производные  и  ; чтоб криволинейный интеграл не зависел от пути интегрирования . Необходимо и достаточно чтоб выполнялось равенство (2).

Док. Не обход. Пусть криволинейный интеграл не зависит от пути интегрирования, а зависит от начальной и конечной точки пути интегрирования.

Возьмём в области D произвольно простую замкнутую кривую Г. На этой кривой т. А и т. В

Т.к. по условию криво-ный интеграл не зависит от пути интегрирования, то интеграл по кривым АmB=AnB

 В силу 1-й теоремы должно выполнятся рав-во (2).

Док. Достат. Пусть выполняется рав-во (2) . Покажем, что криволенейный интеграл не зависит от пути интегрирования :

1-й случай. Берём две произвольные точки принадлежащие области D и соединяем эти точки непрерывными кривыми  и , кот-е не имеют точек самопересечения.

Если эти кривые образуют простой замкнутый контур без самопересечения и т.к. выполняется рав-во (2), то интеграл поэтому замкнутому контуру обязан быть равен 0. ,  т.е. интеграл не зависит от кривой.

2-й случай. Пусть  и  имеют конечное число точек самопересечения

Будем двигаться от А к C1 в результате получили контур и . Аналогично Для всех остальных случаев.

3-й случай. Если кривые пересекаются на счётном множестве точек то интеграл по таким кривым тоже будут равны между собой ….счётное множество эквивалентное множеству натуральных чисел.9.Параметрические ур-я поа-ти, касательная плос-ть, нормаль, направляющие косинусы нормали.

Пусть поверхность задана параметрическими уравнениями :x=x(U,V) ; y=y(U,V); z=z(U,V) и функции x,y,z непрерывны и имеют непрерывные частные произвольные. Рассмотрим матрицу

На поверхности берём точки U0(x0,y0,z0) которая является образом (U0,V0) . Можно показать, что в этом случае уравнение касательной к плоскости поверхности имеет вид А(x-x0)+B(y-y0)+C(z-z0)=0 .Уравнение нормали поверхности . Далее введём направляющую. Пусть поверхность задана параметрическими уравнениями и

l- угол образованный нормалью с направлением осью X

m- угол образованный нормалью с направлением осью Y

n- угол образованный нормалью с направлением осью Z,

cos l cos m cos n - называют направляющими косинусами нормали. Для направляющих косинусов нормали имеет место формула:

, , . В знаменатели стоит двойной знак ± и всякий раз выбирают один из знаков в зависимости от направления нормали. В случае явного задания поверхности направляющие вычисляются , , .

Билет 12

Задача о вычислении массы пространств-го тела.

Пусть в трехмерном пространстве задано тело D, причем в точках этого тела определены некоторые массы и известна плотность распределения массы, кот. явл-ся ф-цией трех переменных U=R(x,y,z).Разобьем это прост-ное тело некоторыми гладкими пов-ми на конечное число областей D1, D2,…,Dn. В каждой области Di произвол. выберем некот. точку (x,h,e)Î Di. Плотность массы в этой точке – это R(xi,hi,ei). Будем считать, что ф-ция R явл-ся непрерывной, а разбиение достат. мелким так, что значения ф-ции внутри области Di не слишком отличаються от значений ф-ции R в выбранной точке. Т.е. будем считать, что в области Di плотность массы одна и та же и равна числу R(xi,hi,ei). Тогда очевидно масса, заключенная в обл. Di , будет равняться R(xi,hi,ei) * DV. Тогда приближенное значение массы для всей области равна S R(xi,hi,ei)*DVi Пусть l - наибольший из диаметров Di – тых областей, а тогда масса , заключенная в области равна m=lim(l®0) S R(xi,hi,ei) * DVi

Пусть теперь задано пространств. тело D. В точках этого тела определена ф-ция U=f(x,y,z). Разобьем это тело на конечное число Di –тых (i=1,2,3,…). В каждой области Di выберем произвол. точку (xi,yi,zi) и составим интегральную

sn=S ò(xi,yi,zi) * DVi Если сущ. предел и он конечный и он не зависит от способа деления обл. D на части и выбора точек (xi,yi,zi) , то этот предел называют тройным интегралом по обл.D от ф-ции f(x,y,z)lim(l®0)sn=òòò f(x,y,z)dx dy dz Следовательноm=òòòR(x,y,z)dxdydz

Св-ва тройного интеграла аналогично св-м двойного интеграла 1) Всякая интегрируемая в обл. D ф-ция ограничена в этой области.

2) Могут быть построены суммы Дарбу

верх St=S Mi * DVi низ st=S mi * DVi

3) Необходимо и достаточное условие сущ. интеграла

lim(l®0)( St-st)=0

4) Как и в случае двойного интеграла сущ. тройной интеграл от любой непрерывной ф-ции, заданной в обл. D. Однако тройной интеграл сущ. и в случае, когда ф-ция f(x,y,z) имеет разрывы 1-го рода на конечном числе пов-тей данного тела D.

5)Тройной интеграл обладает св-вами линейности и аддетивности

òòòDfdx = òòòD1fdx + òòòD2 , где D=D1ÇD2

6)Если сущ. тройной интеграл от ф-ции f, то сущ. интеграл по модулю

и существует равенство

ôòòòô£ òòòôfôdv

Если функция fв области D ограничена какими-то числами m £ f £ М , то для тройного интеграла справидливо неравенство

mVd £òòò ¦dv£M VD

7) Имеет место теорема о среднем , т.е. если функция ¦(x,y,z) не-прерывная в области D , то справедливо равенство

òòò ¦dv = ¦ (X0 , Yo , Z0) (X0 , Yo , Z0)ÎD

Ввычесление тройного интеграла по параллепипеду .