Навигация
Прості функціональні залежності в екології
3.5 Прості функціональні залежності в екології
Розглянемо приклади простих функціональних залежностей, якими оперують в екології. За допомогою засобів Mathcad необхідно буде графічно порівняти траєкторії лінійної, обернено-пропорційної, дрібно-лінійної, статистичної, показової та логарифмічної функції.
1) Створення документа починається з виконання команди Файл=>Новыйй (або <Ctrl+N).
2) Введення тексту (пояснення,коментарю). Натисканням <”> створюємо текстову область і набираємо текст «Залікова робота». Команда Формат=>Текст дозволяє змінювати шрифт (необхідно поміняти Arial → Arial Cyr) і його параметри. Таким же засобом далі створюємо й інші текстові пояснення.
3) Введення формул.
Лінійна залежність
В екології повна лінійна залежність між двома змінюваними величинами зустрічається рідко. В іхтіології, прикладом такої залежності, на ранній стадії розвитку риб, є їхня вага (w), що лінійно залежить від віку (τ) через коефіцієнти (a та b), які характеризують вид та вагу риб на початку спостереження:
w(τ) = a·τ+ b (3.1)
Створимо цю залежність у Mathcad документі та проаналізуємо вплив коефіцієнтів a та b на характер одержуваних лінійних траєкторій. Для цього скористаємося декількома наборами функцій (w1,w2,w3,w4,w5,w6) та коефіцієнтів (a1, b1,a2,b2,a3,b3;…).
Встановимо ЧХ там, де повинно знаходитися перше визначення перемінних і введемо наступну послідовність символів:
а1:0,11 (або а1=0,11) поруч із ним b1:0,18 (або b1=0,18)
Завершувати створення визначень необхідно натисканням клавіші <→>, клавіші <Enter> або виконав щиголь на вільній ділянці документа.
Далі задаємо проміжок зміни τ
t< Ctrl+G>:2,2+.05;6
Тепер задаємо загальне визначення лінійної функції:
w(a,b,t,<Ctrl+G>):a*t<Ctrl+G>+b
Використовуючи отримане значення функції можна розрахувати траєторії при різномінітних коефіцієнтах (a,b):
(w1,w2,w3) – змінюється значення коефіцієнта (a1,a2,a3);
(w4,w5,w6) – змінюється значення коефіцієнта (b2,b3,b4).
4)Побудова графіка. Існує два шляхи побудови графіка:
- скористатися відповідною кнопкою панелі інструментів Графики;
- більш швидкий - натиснути клавіши <Shift+2>. Після цього в документі з’являються дві вкладені рамки. Зовнішня рамка, постачена трьома маркерами зміни розмірів, є межею графічної області і служить для переміщення графіка і зміни його розмірів. Самий графік буде знаходитися у середині меншої рамки, постаченої комірками для формул. Ці комірки призначенні для введення описів, що відповідають,осям. За допомогою клавіші <Tab> можна переходити від однієї комірки опису до іншої.
Введемо τ у якості незалежної перемінної. Потім розмістимо курсор у комірці опису осі ординат і задаємо три функції (w1,w2,w3) розділивши їх, натискуючи клавішу <,> (кома). Далі зробимо щиголь на вільній ділянці документа. Графік готовий.
Щоб змусити Mathcad притримуватися визначених меж зміни незалежної перемінної τ і функцій, їх не обхідно задати на краях абцис та ординат. Таким же чином будуємо графік для залежностей (w4,w5,w6).
- Обернено - пропорційна залежність.
Прикладом використання обернено - пропорційних функцій в екології є залежність типу «хижак-жертва». Зокрема, такі взаємовідносини мають популяції зайців і вовків. У визначений період їхнього розвитку, кількість популяції зайців (z) тим менше, чим більше кількість популяції вовків (V) . Такий зв'язок, через коефіцієнт пропорційності (с) має вид:
![]() (3.2)
(3.2)
Створимо необхідні визначення і проаналізуємо вплив коефіцієнта (с1,с2,сЗ) на вид одержуваних графіків (z1,z2,z3),
v:1,1+1;46
z(c,v):c/v
За допомогою отриманого визначення функції в залежності від коефіцієнта (с1, с2, сЗ) знаходимо траєкторії (z1, z2, z3), після цього будуємо графіки.
- Дрібно - лінійна залежність, формула Михаеліса-Ментен. В екології відомо, що між кількістю страви і швидкістю її споживання мікроорганізмами існує сильна залежність, яку виражають через дрібно-раціональну функцію. Залежність швидкості (М) поглинання мікроорганізмами живильних речовин (субстрату) від його концентрації (s) можна описати відомим рівнянням Михаеліса-Ментен:
![]() (3.3)
(3.3)
де: Mmах - максимальна швидкість поглинання субстрату; Кm - постійна Михаеліса, що дорівнює такої концентрації субстрату, при якій швидкість його поглинання досягає половині максимальної швидкості, тобто
![]()
![]() Графіком функції є гіпербола то називається гіперболою Михаеліса. Коли концентрація субстрату необмежено збільшується (s→∞) швидкість поглинання прагне до постійної величини
Графіком функції є гіпербола то називається гіперболою Михаеліса. Коли концентрація субстрату необмежено збільшується (s→∞) швидкість поглинання прагне до постійної величини
Така пряма, до якої зменшується відстань від точок кривої, які проеціруються в безкраїсть, називається асимптотою.
Створимо необхідні визначення і проаналізуємо вплив коефіцієнтів (Кm1, Кm2, КmЗ) і (Мmах2, МmахЗ, Мmах4) на вид одержуваних траекторій Кривих.
![]()
М(Мmax,Km,s):Mmax*s/Km+s
За допомогою отриманого визначення функції розрахуємо поведінку функції (М1, М2, МЗ) змінюючи значення коефіцієнта (Кm1 , Km2. Кm3); (М4, М5, М6) - змінюючи значення коефіцієнта (Мmах2, МmахЗМmах4) . Після цього побудуємо графіки.
- Статечна залежність. Раніше було розглянуто, що іноді в іхтіології вага особі у ранньому періоді розвитку, може бути описано лінійною функцією. Для опису більш тривалих періодів розвитку особі, замість лінійної, часто застосовують статечну залежність:
![]() (3.5)
(3.5)
Створимо цю залежність і в Маthcad - документі проаналізуємо вплив коефіцієнтів (a і b) на вид одержуваних графіків:
t<Ctrl+G>:2,2+.01;6
w (a,b,t<Ctrl+G>):a*(t<Ctrl+G>^b<пробіл>+1)
Натискання клавіші <пробіл> необхідно, щоб Маthcad міг визначити, що b повинна бути додана до значення τ , а не до показника ступеня b.
Використовуючи створене визначення функції розраховують траєкторії кривих для функцій (w1, w2, w3) змінюючи значення коефіцієнта (а1, а2, аЗ); для функцій (w4,w5,w6) - змінюється значення коефіцієнта (b2, bЗ, b4). Отримані результати відображають на графіках.
- Показова і логарифмічна залежності, при. визначенні показової залежності в якості аргументу (наприклад, х) виступає показник ступеня:
![]() (3.6)
(3.6)
Оберненою для показової функції є логарифмічна:
![]()
(3.7)
Графіки логарифмічної функції мають таку ж форму, як і графіки показової функції, але вони розташовані стосовно останніх симетричнощодо осі х (показові – y).
Коли в показовій функції за підставу ступеня а прийняте ірраціональне число е=2,71828, то залежність називається експоненціальна. Логарифмічна функція з основою, яка рівна числу е називається натуральним логарифмом (у=ln(x)). При вивченні різноманітних природних процесів, включаючи і біологічні, найбільш часто зустрічаються залежності між перемінними величинами, що описуються показовими і логарифмічними функціями з основою е. Розглянемо декілька прикладів застосування такого виду функцій.
а) Для більшості біологічних процесів, у тому числі і розмноження різноманітних популяцій, значення змінної, що характеризує чисельність популяції, не може необмежено збільшуватися. Для опису таких процесів добре пристосована показова функція з від'ємним показником. Чисельність більшості популяцій спочатку збільшується, а потім залишається постійною і не перевищує деякої величини Nmax:
![]() (3.8)
(3.8)
де κ - коефіцієнт, що визначається експериментально для кожного виду популяції; N0 - початкова чисельність популяції. Пряма N=Nmаx є горизонтальною асимптотою графіка цієї функції, а величина Мmах -називається "ємність середовища".
Збудуємо цю залежність і в Маthcad -документі проаналізуємо вплив коефіцієнта (κ) на вид одержуваних графіків:
N0:=200
Nmax:1500
t:0,0+.01;10
N(N0,Nmax,k,t):N0+(Nmax-N0)*(1-e^-k*t<пробіл>)
Для побудови графіків використовують значення функцій (N1, N2,: N3), що розраховані при різноманітних значеннях коефіцієнтів (кі, к2, кЗ).
б) Приклад, пов'язаний з дією на організм тварин шкідливих речовин (токсинів), що скорочують тривалість їх життя. Якщо дозу речовини, що діє на організм позначити через р, середню тривалість життя тварин позначити через Тm і врахуємо дію великої кількості токсичних речовин (p→∞), що скорочують тривалість життя Т до величини Tp, то процес дії шкідливої речовини добре описується наступною показовою функцією:
![]() |
|
в) Приклад, у якому для кращого математичного опису процесів збільшення ваги морських тварин застосовується формула Верталанфі, тобто комбінація показової і статечної функції:
![]() (3.10)
(3.10)
де Wmax - найбільша вага риби; α та t0 - експериментально обумовлені коефіцієнти.
3.6 Зберігання документа
Скориставшись командою Файл=>Сохранить можна привласнити створеному документу ім’я (або комбінація клавіш <Crtl+S>). Розширення mcd буде дано автоматично. Зберегти документ під новим ім’ям або іншій папці (диску) можна за допомогою команди Файл=>Сохранить как.
Похожие работы
... провідності твердих електролітів ясно відображає специфіку «твердості», оскільки рідкі іонопровідні розчини такого роду анізотропією не володіють. МЕТОДИ ВИЯВЛЕННЯ СУПЕРІОННОЇ ПРОВІДНОСТІ Отже, існування феномена суперіонної проводности твердо встановлене і не викликає ніяких сумнівів. Одночасно з цим очевидна непридатність традиційної й опробованої кількісної теорії для його описання. ...
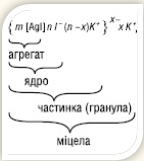
... ії Метод конденсації полягає в утворенні нерозчинних сполук за допомогою реакцій обміну, гідролізу, відновлення, окислення. Здійснюючи ці реакції в сильно розбавлених розчинах і з деяким надлишком одного з компонентів, дістають не осади, а колоїдні розчини. До конденсаційних методів належить також добування ліозолів за допомогою заміни розчинника. Наприклад, колоїдний розчин каніфолі можна ...
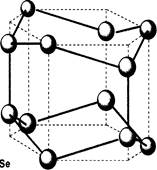
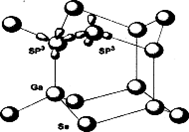
... відповідності із структурними характеристиками, гратки- "господарі" схематично можна розділити на три різні групи одновимірні, що містять структурні елементи ланцюгового типу; двовимірні, утворені структурними елементами шаруватої матриці(гостьові позиції знаходяться в енергетичній щілині ван-дер-ваальса, розташованій між сусідніми шарами); тривимірні - 3^, з сотовою матрицею. У випадку одно - і ...
... параметрів при термоциклюванні, а саме ця особливість є принциповою для практичного використання. Перспективними для вирішення проблеми деградації об’ємних матеріалів з ФПМН є склокерамічні матеріали на основі компонента з фазовим переходом метал-напівпровідник. Такі матеріали можна отримати за керамічною технологією. Важливою вимогою до них, окрім стабільної поведінки при термоциклюванні, є ...



0 комментариев