Навигация
3.2 Задача №2
Потрібно інтерполювати (використовуючи задачу першого або другого роду) одну з відомих функцій, з допомогою кубічних В-сплайнів, у випадку нерівномірної сітки розбиття.
Розв’язання: Для розв’язання цієї задачі візьмемо функцію ![]() і будемо її інтерполювати на відрізку
і будемо її інтерполювати на відрізку ![]() , розбивши його на 5 частин ([0,1], [1,9/5], [9/5,12/5], [12/5,14/5], [14/5,3]). Маємо нерівномірну сітку, отже будемо користуватися формулою (15). Знайдемо
, розбивши його на 5 частин ([0,1], [1,9/5], [9/5,12/5], [12/5,14/5], [14/5,3]). Маємо нерівномірну сітку, отже будемо користуватися формулою (15). Знайдемо ![]() і
і ![]() (задача інтерполяції першого роду). Аналогічно, як і в першій задачі використаємо формули (34) і розв’яжемо систему (33). Для нашої функції
(задача інтерполяції першого роду). Аналогічно, як і в першій задачі використаємо формули (34) і розв’яжемо систему (33). Для нашої функції ![]() маємо наступні дані:
маємо наступні дані:
|
|
|
|
|
| -2 | -2 |
| |
| -1 | -1 |
| |
| 0 | 0 | 1 | 1 |
| 1 | 1 |
| |
| 2 |
|
| |
| 3 |
|
| |
| 4 |
|
| |
| 5 | 3 |
|
|
| 6 | 3,1 |
| |
| 7 | 3,2 |
|
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() .
.
Тоді тридіагональна матриця ![]() і вектор
і вектор ![]() відповідно дорівнюватимуть:
відповідно дорівнюватимуть:
 ,
,![]() , підставивши
, підставивши
їх у матричне рівняння, отримаємо вектор ![]() :
:
![]()
![]() ,
,![]() . Отже, маємо інтерполяційний сплайн функції
. Отже, маємо інтерполяційний сплайн функції ![]() на проміжку
на проміжку ![]() :
: 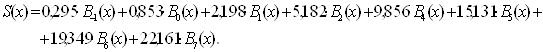
Побудуємо його графік (в середовищі Matlab):
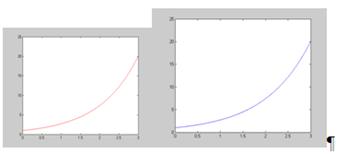
Мал. 10 і 11 – Графік функції
На малюнку 10 зображено графік функції ![]() , а на малюнку 11 – графік функції
, а на малюнку 11 – графік функції ![]() (зображено синім кольором), яка накладається на графік функції
(зображено синім кольором), яка накладається на графік функції ![]() . Як бачимо наш інтерполяційний сплайн фактично повністю співпадає з
. Як бачимо наш інтерполяційний сплайн фактично повністю співпадає з ![]() і лише при великому збільшенні можна побачити розбіжності (малюнок 12 і 13), тобто має місце незначна похибка. Знайдемо її.
і лише при великому збільшенні можна побачити розбіжності (малюнок 12 і 13), тобто має місце незначна похибка. Знайдемо її.
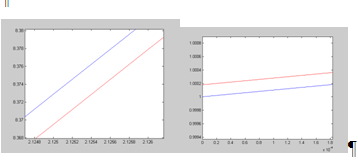
Мал. 12, 13 – Розбіжності
Для цього будемо шукати максимальну похибку на кожному з відрізків розбиття. Скористаємося наступними формулами:
![]() ,
,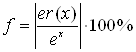 (36)
(36)
Неозброєним оком похибки не видно, але вона є, і це показано на малюнку 14, який зображає функцію ![]() на кожному проміжку розбиття.
на кожному проміжку розбиття.



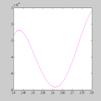
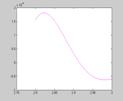
Мал. 14 – Похибки
Аналогічно, як і в попередній задачі розглядаємо всі проміжки розбиття і знаходимо максимальні значення похибок на кожному з них, які представлені в наступній таблиці:
Таблиця 5. - Всі проміжки розбиття
| сегмент |
|
|
|
| [0,1] | 0,5 | 1,786 | 0,1049% |
| [1, | 1,38 | -3,141 | 0,0682% |
| [ | 2,12 | -1,431 | 0,0228% |
| [ | 2,63 | 1,548 | 0,0028% |
| [ | 2,82 | 1,813 | 0,0002% |
З таблиці видно, що максимальна похибка менша за 0,11%, і, оскільки, задовільною вважається похибка менша чим 5%, то отримана нас повністю задовольняє. Ще можна відзначити, що найменша величина похибки досягається на найменшому із сегментів розбиття, тобто чим менші проміжки розбиття тим більша точність (але розбиття на занадто малі сегменти може значно ускладнити обрахунки).
Висновки
У курсовій роботі було розглянуто лінійні , квадратичні та кубічні В-сплайни. Було отримано форми запису цих сплайнів та виведено деякі формули для розрахунків інтерполяційних задач. А також представлені рекурентні формули для виведення В-сплайнів 1-го, 2-го, 3-го та вищих порядків.
Із розглянутих сплайнів найкращі інтерполяційні якості мають кубічні В-сплайни, тому що саме вони забезпечують задовільну гладкість, на відмінно від лінійних і квадратичних В-сплайнів, а також для кубічних В-сплайнів використовуються порівняно нескладні обчислення, що не скажеш про сплайни вищих порядків, які до того ж можуть мати небажані скачки.
Необхідно відмітити перевагу В-сплайнів над звичайними сплайн-функціями. В-сплайни складаються з сегментів кривих, залежних тільки від кількох вузлових точок, і тому при локальних змінах крива змінюється лише на одному сегменті, ніяк не впливаючи на криві на інших сегментах.
Як було перевірено на практиці кубічні В-сплайни забезпечують дуже високу точність у розрахунках, яка складає менше ніж 0,2%, в той час як задовільною вважається похибка не більше 5%.
Отже, хоч кубічні В-сплайни, і є методом важчим у розрахунках ніж інші відомі методи, які застосовуються у задачах для наближення, але він дає набагато точніший результат, і є просто незамінним при розв’язуванні задач, які неможливо розв’язати іншими методами. Це дуже важливо, і тому В-сплайни доцільно вивчати у ВНЗ, щоб студенти могли розв’язувати, нерозв’язні раніше, задачі, і отримувати результати високої точності.
Кубічні В-сплайни мають численні застосування як в математичній теорії, так і в різноманітних обчислювальних задачах. Сплакни застосовують при вивченні «Чисельних методів», як додатковий метод інтерполяції, та при розв’язуванні рівнянь математичної фізики. Особливо зручно з допомогою сплайн-функцій розв’язувати апроксимаційні та інтерполяційні задачі.
Список використаних джерел
1. Корнейчук Н. П. Сплайны в теории приближения. / Н. П. Корнейчук. – М. : Наука, 1984. – 352с.
2. Сплайн – интерполяция. // Електронний ресурс: http://petrsu.karelia.ru/psu/Deps/IMO/Complex/part3/part34_a.htm
3. Калиткин Н. Н. Численные методы. / Н. Н. Калиткин. – М. : Нака, 1978. – 512с.
4. Селиванова И. А. Интерполяция сплайнами. / И. А. Селиванова.–Свердловск: УПИ, 1989. – 11с.
5. Пак Т. В. Лабораторные работы по Численным методам. / Т. В. Пак. Учебно-методическое пособие. – Владивосток: Изд-во Дальневост. ун-та, 2006. – 24с.
6. Завьялов Ю. С. Методы сплайн-функций. / Ю. С. Завьялов, Б. И. Квасов, В. Л. Мирошниченко. – М. : Наука, 1980. – 280с.
7. В-сплайн. // Електронний ресурс: http://uk.wikipedia.org/wiki/B-сплайн
8. Шикин Е. В. Кривые и поверхности на экране компьютера. / Е. В. Шикин, Л. П. Плис. Руководство по сплайнам для пользователей. – М. : ДИАЛОГ-МИФИ, 1996. – 240с.
9. В-сплайны. // Електронний ресурс: http://www.masters.donntu.edu.ua/2005/kita/tribrat/library/splines.htm
0 комментариев