Навигация
Последовательность решения задачи
1.3 Последовательность решения задачи
Определяются номера вариантов исходных данных применительно к табл. 1.3 и 1.4. Для этого две последние цифры зачетной книжки студента делятся с остатком на количество вариантов, представленных в таблицах. К остатку от деления прибавляется единица. Полученное число явится номером варианта для информации соответствующего вида.
Например, считываем из зачетной книжки число 89. Применительно к табл. 1.3 делим его на 5. Получаем 17 и 4 в остатке. Прибавляем к остатку единицу, получаем вариант 5. Если остаток 0, вариант 1.
Таблица 1.4
| Номер варианта | Объемы ресурсов | ||||
| рабочая сила | материалы | фонд времени | специальные запчасти | электроэнергия | |
| 1 2 3 4 5 6 7 8 9 10 | 650000 590000 680000 700000 750000 690000 800000 790000 770000 710000 | 100000 98000 120000 125000 130000 133000 129000 130000 115000 120000 | 125000 80000 90000 75000 88000 74000 95000 80000 92000 79000 | 5000 6000 7000 8000 9000 7800 10000 9600 8100 7900 | 6300 7000 6500 6900 7000 7400 9200 8400 7500 7800 |
Для соответствующих исходных данных составляется экономико-математическая модель.
Используя надстройку «Поиск решения» пакета EXCEL решается задача с выдачей отчета «Результаты».
Полученное решение анализируется, и делаются выводы, в которых дается характеристика найденному оптимальному варианту производственной программы вагоноремонтного предприятия и эффективности использования производственных ресурсов.
2. ОПТИМИЗАЦИЯ ЗАГРУЗКИ МОЩНОСТЕЙ ПО ПРОИЗВОДСТВУ ЗАПАСНЫХ ЧАСТЕЙ ДЛЯ ПРЕДПРИЯТИЙ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
2.1 Постановка задачи
Железнодорожный транспорт в больших объемах потребляет разнообразные запасные части для поддержания активной части своих производственных фондов в работоспособном состоянии. Запасные части для предприятий железнодорожного транспорта изготавливаются на заводах по ремонту подвижного состава и производству запасных частей и других специализированных предприятиях. Снижение издержек, связанных с обеспечением предприятий железнодорожного транспорта запасными частями весьма актуально. Учитывая большую протяженность железных дорог России, эта задача должна решаться комплексно как для производственной, так и для транспортной составляющей затрат. Для решения этой задачи с успехом может быть использована экономико-математическая модель так называемой «Транспортной задачи линейного программирования» [1, 3, 9]. В частности ее разновидность – открытая модель транспортной задачи. Для построения экономико-математической модели рассматриваемой задачи введем следующие обозначения:
Аi – производственные мощности предприятий по производству запасных частей по пунктам размещения i;
Вj – потребности в запасных частях в пунктах j;
Хij – объемы перевозок запасных частей между пунктами производства и пунктами потребления i, ,j;
Зi – затраты на производство единицы (удельные затраты) запасных частей у предприятий по пунктам i;
Сij – затраты на транспортировку единицы запасных частей между пунктами производства и потребления;
аi – загрузка производственных мощностей предприятий по производству запасных частей по пунктам размещения i.
Тогда экономико-математическая модель может быть сформулирована следующим образом: найти совокупность переменных аi, минимизирующих целевую функцию F.
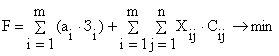 (2.1)
(2.1)
После некоторых преобразований формула (2.1) принимает вид:
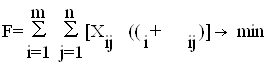 .
.
На целевую функцию накладываются следующие ограничения:
![]() Хij = аi, i = 1,2,…,m; (2.2)
Хij = аi, i = 1,2,…,m; (2.2)
![]() Хij = Вj, j = 1,2,…,n; (2.3)
Хij = Вj, j = 1,2,…,n; (2.3)
![]() Аi >
Аi > ![]() Вj (2.4)
Вj (2.4)
аi, Хij > = 0 для всех значений индексов (2.5)
Ограничения 2.2 и 2.3 называются балансовыми. Они показывают, что вся произведенная продукция по пунктам размещения мощностей должна быть вывезена – ограничение 2.2, а спрос потребителей должен быть полностью удовлетворен – ограничение 2.3. Ограничение 2.5 показывает, что суммарная мощность всех предприятий должна превышать общие потребности. Это весьма важно, поскольку при равенстве задача оптимизации теряет смысл, так как будет иметь место только один вариант решения, при стопроцентной загрузке мощностей. Из ограничений 2.2 и 2.3 следует, что
![]() а =
а = ![]() В.
В.
А из ограничения 2.5:
![]() А >
А > ![]() а.
а.
Ограничение 2.5 называется ограничением неотрицательности переменных.
Похожие работы
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
... , вызвало необходимость анализа и обобщения теоретических основ математического моделирования народнохозяйственных процессов. Вклад представителей экономико-математической школы в развитие мировой экономической мысли очень велик. Признанный мировой экономической наукой и практикой феномен российской интеллектуальной мысли - разработка теоретических экономических идей, основанных на применении ...
... а также дотирования субъектами РФ убытков от пригородных перевозок. Таким образом, реформа предусматривает сохранение единой государственной системы железных дорог РФ, централизации управления перевозочным процессом и безопасностью движения в условиях разделения функций государственного и хозяйственного регулирования. В будущем, впрочем, вполне вероятно строительство не только подъездных путей, ...
... это планируется сделать на основных направлениях пассажирских перевозок и на линиях, входящих в международные транспортные коридоры, на которых также предусматривается организация контейнерных перевозок. Влияние железнодорожного транспорта на социально-экономическое развитие Вологодской области. Для того, чтобы оценить влияние железных дорог на население и хозяйство области был выбран метод ...




0 комментариев