Навигация
2.3 Исходные данные
Исходная информация для решения задачи включает в себя показатели, входящие в модель 2.1–2.5. Среди них можно выделить три группы исходных данных.
Первая группа – это показатели производственных мощностей по пунктам их размещения. К ним относятся собственно мощности предприятий по производству запасных частей – Аi и удельные затраты на производство – Зi. Мощности предприятий приведены в табл. 2.4.
Таблица 2.4
| Ai | Мощности по производству запасных частей в тоннах по вариантам | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| A1 | 490 | 500 | 550 | 670 | 1000 | 450 | 670 | 540 | 640 | 570 |
| A2 | 380 | 350 | 690 | 500 | 390 | 600 | 300 | 760 | 290 | 930 |
| A3 | 600 | 640 | 370 | 850 | 740 | 840 | 880 | 580 | 850 | 810 |
| A4 | 750 | 850 | 950 | 450 | 600 | 760 | 490 | 670 | 700 | 350 |
| A5 | 800 | 700 | 450 | 620 | 520 | 620 | 750 | 450 | 580 | 490 |
Удельные затраты на производство рассчитываются по формуле:
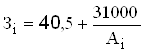 (тыс. руб.). (2.6)
(тыс. руб.). (2.6)
Вторая группа показателей – это потребности в запасных частях по пунктам размещения потребителей в тоннах – Вj. Эти данные по вариантам приведены в табл. 2.5.
Третья группа показателей – это затраты на транспортировку запасных частей между пунктами производства и потребления на рассматриваемом полигоне железнодорожной сети. Полигон железнодорожной сети представлен табл. 2.6. Применительно к заданному полигону по вариантам задаются номера узлов железнодорожной сети, в которых размещены предприятия по производству запасных частей (индексы i), и номера узлов, в которых размещены потребители запасных частей (индексы j) (табл. 2.7).
Расчет минимальных транспортных затрат между пунктами производства и потребления осуществляется по формуле:
![]() (тыс. руб.), (2.7)
(тыс. руб.), (2.7)
где е – расходная ставка на 10 ткм. Для рассматриваемого рода груза принимается равной 80 руб.; L – минимальное расстояние, рассчитываемое для заданного полигона между пунктами производства и потребления, км.
Таблица 2.5
| Пункты потребления j | Потребности пунктов потребления по вариантам (т) | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 470 | 540 | 240 | 390 | 480 | 460 |
| 2 | 330 | 290 | 430 | 600 | 340 | 840 |
| 3 | 560 | 420 | 620 | 350 | 560 | 430 |
| 4 | 610 | 600 | 320 | 780 | 500 | 590 |
| 5 | 220 | 310 | 790 | 620 | 700 | 300 |
| 6 | 650 | 460 | 600 | 370 | 210 | 450 |
| 7 | 490 | 720 | 400 | 410 | 520 | 510 |
| 8 | 670 | 860 | 610 | 650 | 670 | 680 |
| 9 | 700 | 450 | 730 | 720 | 790 | 520 |
| 10 | 460 | 300 | 540 | 300 | 460 | 400 |
Таблица 2.6
| Номера узлов | 1–2 | 1–3 | 1–4 | 2–3 | 2–6 | 2–10 | 3–5 | 3–7 | 3–8 | 4–5 |
| Расстояние, км | 110 | 75 | 90 | 160 | 69 | 130 | 150 | 170 | 130 | 98 |
| Номера узлов | 5–8 | 5–9 | 6–7 | 6–10 | 7–8 | 7–11 | 8–9 | 8–12 | 7–8 | 7–11 |
| Расстояние, км | 49 | 112 | 125 | 98 | 117 | 135 | 100 | 95 | 117 | 135 |
| Номера узлов | 8–9 | 8–12 | 9–12 | 9–13 | 10–11 | 10–14 | 11–12 | 11–14 | 12–13 | 12–15 |
| Расстояние, км | 100 | 95 | 110 | 113 | 95 | 117 | 150 | 105 | 190 | 170 |
| Номера узлов | 13–15 | 14–15 | 14–16 | 15–16 | ||||||
| Расстояние, км | 200 | 140 | 79 | 130 |
Таблица 2.7
| Варианты | Номера узлов размещения мощностей – индексы i | Номера узлов размещения потребителей – индексы j | |||||||||||||
| 1 | 1 | 8 | 10 | 13 | 16 | 2 | 3 | 5 | 6 | 7 | 9 | 11 | 12 | 14 | 15 |
| 2 | 3 | 5 | 6 | 13 | 14 | 1 | 2 | 4 | 7 | 8 | 9 | 10 | 11 | 12 | 16 |
| 3 | 2 | 4 | 7 | 9 | 15 | 3 | 5 | 8 | 6 | 10 | 11 | 12 | 13 | 14 | 16 |
| 4 | 1 | 5 | 6 | 11 | 16 | 2 | 3 | 7 | 8 | 9 | 10 | 12 | 13 | 14 | 15 |
2.4 Последовательность решения задачи
Решение задачи осуществляется по вариантам применительно к табл. 2.4, 2.5 и 2.7. Расчет вариантов должен быть приведен в работе. Выполнение задачи осуществляется в следующем порядке.
1. Постановка задачи и формулировка экономико-математической модели в соответствии с заданной размерностью.
2. Определение показателей производственных мощностей. Величины мощностей берутся из табл. 2.4, а производственные затраты рассчитываются по формуле 2.6.
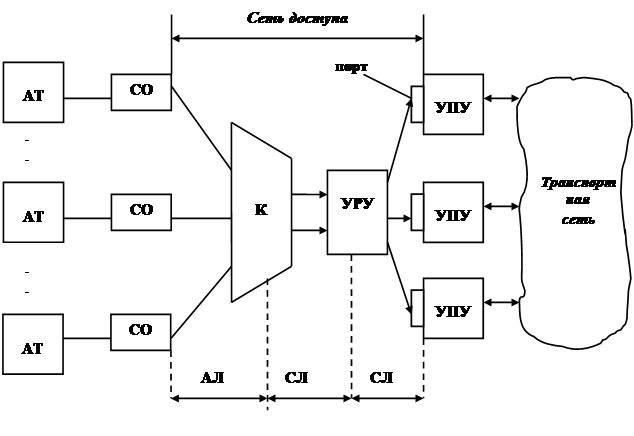
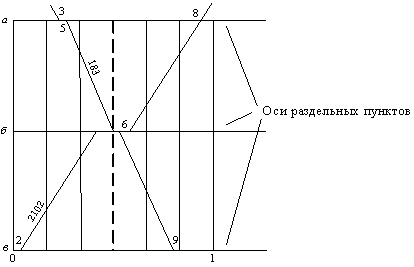
3. Расчет затрат на транспортировку единицы запасных частей между пунктами производства и потребления. Для этого по табл. 2.7 строится схема рассматриваемого полигона железных дорог – транспортная сеть, как это показано на фрагменте (рис. 11).
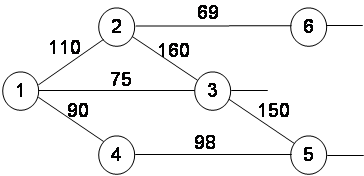
Рис. 11
На транспортной сети по соответствующему варианту выделяются узлы, в которых размещены производственные мощности и потребители запасных частей. Далее непосредственно по сети рассчитываются кратчайшие расстояния между каждым пунктом производства и потребления.
Результаты расчета заносятся в таблицу формы соответствующей табл. 2.1. Затраты на транспортировку рассчитываются по формуле 2.7 в таблице аналогичной формы.
4. Построение расчетной матрицы. Расчетная матрица, соответствующая табл. 2.2, строится на основе подготовленных ранее исходных данных. По существу она представляет собой экономико-математическую модель решаемой задачи в матричной форме.
5. Расчет оптимального плана транспортной задачи для расчетной матрицы. Расчет может быть выполнен вручную [2, 3, 4, 7], либо с применением соответствующих программных продуктов. Рекомендуется использовать для этой цели средства EXCEL «Поиск решения», как это было показано ранее с приложением листинга. Результат решения транспортной задачи оформляется согласно табл. 2.3.
6. Расчет показателей оптимального плана загрузки производственных мощностей. Показатели загрузки мощностей по каждому пункту определяются по строкам расчетной матрицы, в которой представлен результат решения транспортной задачи. Загрузка будет равна объему поставок продукции реальным потребителям, то есть без фиктивного. Далее рассчитываются затраты в целом по оптимальному плану и, в том числе, на производство и транспортировку продукции.
7. Анализ показателей оптимального плана и выводы.
3. ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА (МОДЕЛЬ «ЗАТРАТЫ–ВЫПУСК»)
3.1 Методика решения задачи
Эффективное функционирование экономики предполагает наличие баланса между отдельными отраслями. Каждая отрасль при этом выступает двояко: с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продуктов, вырабатываемых другими отраслями. Для наглядного выражения взаимной связи между отраслями используют таблицы определенного вида, которые называют таблицами межотраслевого баланса.
Рассмотрим наиболее простой вариант модели межотраслевого баланса (модель Леонтьева, или модель «затраты–выпуск»).
Алгебраическая теория анализа «затраты–выпуск» сводится к системе линейных уравнений, в которых параметрами являются коэффициенты затрат на производство продукции.
Пусть весь производственный сектор народного хозяйства разбит на n чистых отраслей. Чистая отрасль (это условное понятие) – некоторая часть народного хозяйства, более или менее цельная (например, энергетика, машиностроение, сельское хозяйство и т. п.).
Пусть xij – количество продукции i-й отрасли, расходуемое в j-й отрасли; xi – объем производства i-й отрасли за данный промежуток времени, так называемый валовой выпуск продукции i; yi – объем потребления продукции i-й отрасли в непроизводственной сфере, объем конечного потребления; zj – условно чистая продукция, которая включает оплату труда, чистый доход и амортизацию.
Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки и т. п.), или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевые балансы. Мы будем рассматривать стоимостной баланс.
В табл. 3.1 отражена принципиальная схема межотраслевого баланса в стоимостном выражении.
Таблица 3.1
| Производящие отрасли | Потребляющие отрасли | Конечный продукт | Валовой продукт | |||
| 1 | 2 | ….. | n | |||
| 1 2 …. N | X11 X21 …. Xn1 | X12 X22 …. Xn2 | …. …. …. …. | X1n X2n …. Xnn | y1 y2 …. yn | X1 X2 …. Xn |
| Условно чистая продукция | Z1 | Z1 | …. | Z1 |
| |
| Валовой продукт | X1 | X2 | …. | Xn |
| |
Во-первых, рассматривая схему баланса по столбцам, можно сделать очевидный вывод, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения:
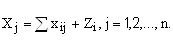 (3.1)
(3.1)
Величина условно чистой продукции Z, равна сумме амортизации, оплаты труда и чистого дохода j-й отрасли. Соотношение (1) охватывает систему из п уравнений, отражающих стоимостной состав продукции всех отраслей материальной сферы.
Во-вторых, рассматривая схему МОБ по строкам для каждой производящей отрасли, можно видеть, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:
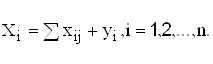 (3.2)
(3.2)
Формула (3.2) описывает систему из n уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования.
Балансовый характер таблицы выражается в том, что:
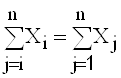 .
.
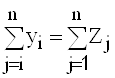 .
.
Основу экономико-математической модели МОБ составляет матрица коэффициентов прямых материальных затрат А = (аij).
Коэффициент прямых материальных затрат аij показывает, какое количество продукции i-й отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции j-й отрасли:
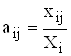 , i,j = 1, 2, …, n. (3.3)
, i,j = 1, 2, …, n. (3.3)
Формула 3.3 предполагает следующие допущения.
Первое состоит в том, что сложившуюся технологию производства считаем неизменной. Таким образом, матрица А = (аij) постоянна.
Второе состоит в постулировании свойства линейности существующих технологий, т. е. для выпуска j-й отраслью любого объема продукции Xj,- необходимо затратить продукцию отрасли i в количестве аijXj,-, т. е. материальные издержки пропорциональны объему производимой продукции:
![]() . (3.4)
. (3.4)
Подставляя (3.4) в балансовое соотношение (3.2), получаем
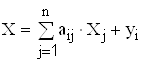 (3.5)
(3.5)
![]()
или в матричной форме
![]() . (3.6)
. (3.6)
С помощью этой модели можно выполнять три вида плановых расчетов.
•Задав в модели величины валовой продукции каждой отрасли (X,-), можно определить объемы конечной продукции каждой отрасли (Y,):
![]() . (3.7)
. (3.7)
• Задав величины конечной продукции всех отраслей (Yi), можно определить величины валовой продукции каждой отрасли (Xi):
![]() . (3.8)
. (3.8)
•Для ряда отраслей задав величины валовой продукции, а для всех остальных – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.
В формулах (3.7) и (3.8) Е обозначает единичную матрицу n-го порядка, а (E-A)–1 –матрицу, обратную матрице (Е - А). Если определитель матрицы (Е - А) не равен нулю, т. е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим эту обратную матрицу через В = (Е- А)–1 тогда систему уравнений в матричной форме (3.8) можно записать в виде
![]() . (3.9)
. (3.9)
Элементы матрицы В называются коэффициентами полных материальных затрат. Они показывают, сколько всего нужно произвести продукции n-й отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. норма больше единицы.
Пример
Даны коэффициенты прямых затрат aij и конечный продукт Уi,- для трехотраслевой экономической системы:
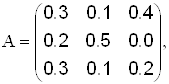
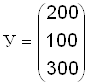
Требуется:
Похожие работы
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
... , вызвало необходимость анализа и обобщения теоретических основ математического моделирования народнохозяйственных процессов. Вклад представителей экономико-математической школы в развитие мировой экономической мысли очень велик. Признанный мировой экономической наукой и практикой феномен российской интеллектуальной мысли - разработка теоретических экономических идей, основанных на применении ...
... а также дотирования субъектами РФ убытков от пригородных перевозок. Таким образом, реформа предусматривает сохранение единой государственной системы железных дорог РФ, централизации управления перевозочным процессом и безопасностью движения в условиях разделения функций государственного и хозяйственного регулирования. В будущем, впрочем, вполне вероятно строительство не только подъездных путей, ...
... это планируется сделать на основных направлениях пассажирских перевозок и на линиях, входящих в международные транспортные коридоры, на которых также предусматривается организация контейнерных перевозок. Влияние железнодорожного транспорта на социально-экономическое развитие Вологодской области. Для того, чтобы оценить влияние железных дорог на население и хозяйство области был выбран метод ...
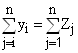




0 комментариев