Навигация
Получение квадратичной модели
1.1.3 Получение квадратичной модели
Уравнение квадратичной системы имеет вид:
![]()
Матрицы с подстановкой номинального режима:
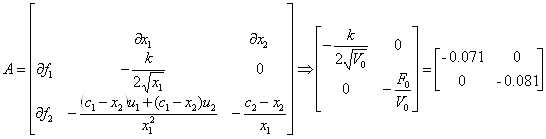
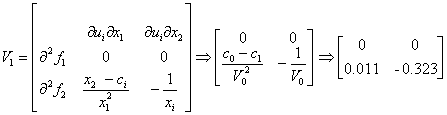
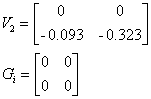
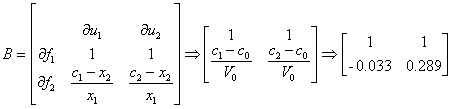
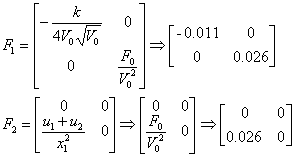
1.1.4 Запись билинейной модели
Уравнение билинейной системы записывается в виде
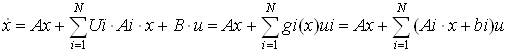
Приняв допущение, что критерий оптимальности в форме О.А. Красовского
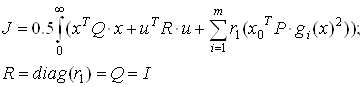
регулятор определяется по зависимости ![]()
Где матрица определена как ![]()
1.1.5 Линеаризованная модель
Линеаризуем зависимость ![]() , разложив ее на ряд Тейлора.
, разложив ее на ряд Тейлора.
![]()
![]()
![]()
![]()
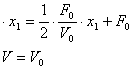
С учетом ранее изложенного запишем:
![]()
![]() ; (т.к.
; (т.к. ![]() ), где
), где ![]() ;
;
![]()
Припустив в случае остатка ![]() . Тогда, подставив производную
. Тогда, подставив производную ![]() , получим
, получим
![]()
![]()
![]()
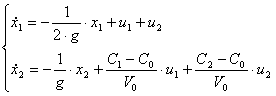
Представим систему в матричной форме:
![]()
Тогда матрицы А и В запишутся в виде
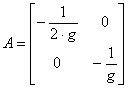 ,
, 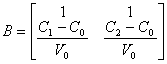
Для определения матрицы С необходимо установить связь между векторами x и y. Т.к. ![]() ,
, ![]() , то
, то
![]() ;
; ![]()
![]() , то
, то ![]()
Тогда
![]()
Система будет иметь вид
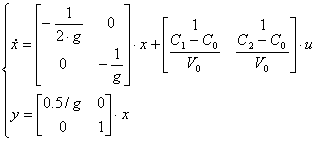
Коэффициенты модели системы:
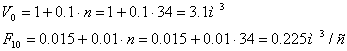

![]()
![]()
![]()
1.1.6 Модель в дискретном времени
Система в дискретном времени имеет вид:
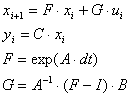
dt= 24 c.
![]()
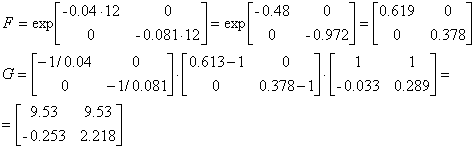
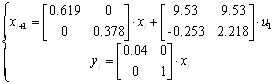
Зададим ![]() ,
, ![]() , получим значения на выходах дискретной системы.
, получим значения на выходах дискретной системы.
Таблица 4 Значение выходов дискретной системы
| Возмущение | Реакция выхода системы y(t) | |||||||
| u1=0.01 u2=0 | y1 y2 | 0 0 | 0.00384 -0.00254 | 0.00624 -0.00352 | 0.0077 -0.03896 | 0.00859 -0.004038 | 0.00913 -0.00409 | 0.00947 -0.00411 |
| время t, с | 0 | 12 | 24 | 37 | 49 | 61 | 74 | |
Похожие работы
... выставляться с понижающим коэффициентом 0,8. 7. Студент должен быть вежливым, терпимым, открытым, доброжелательным к преподавателям и студентам. Тема 1. Введение. Структура и содержание дисциплины «Основы патентоведения и рационализации» Цель: знакомство с задачами изучаемой дисциплины, с основными понятиями и определениями. План: 1.1 Изобретательство – основа развития ...
0 комментариев