Построение графиков кривой разгона нелинейной системы

1.3.3 Построение графиков кривой разгона нелинейной системы

Данные для построения графиков получены в пункте 1.1.2

Для первого выхода пользуемся таблицей 1. Получившиеся графики можем сопоставить с графиками полученным в пункте 1.3.1, введя поправку на начальное значение параметра

Рисунок 11 – Реакция первого выхода на возмущения u1(t) в пункте 1.3.1

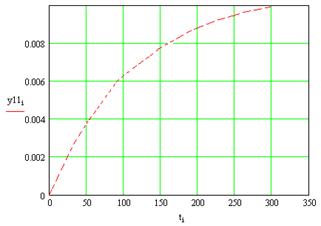
Рисунок 12 – Реакция первого выхода на возмущение для линеаризованной системы

Легко видеть, что эти график совпадают, что говорит о том, что линеаризация по первому выходу проведена на приемлемом уровне

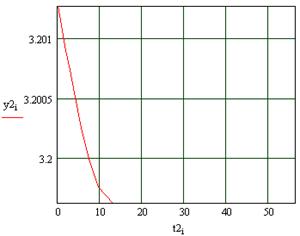
Рисунок 14 – Реакция второго выхода на возмущения u1(t) полученного в пункте 1.3.1

Рисунок 13 – Реакция второго выхода на возмущения для линеаризованной системы

В данном случае имеет место погрешность которую можно связать с ошибкой вносимой кусочно – линейной аппроксимации.

1.3.4 Установившиеся состояния системы

Вычислить постоянное значение состояния системы в условиях

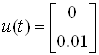
Т.к. установившееся значение предполагает отсутствие динамики, то систему можно записать в следующем виде

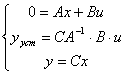
1.4 Идентификация многомерной математической модели по данным эксперимента

1.4.1 Активная идентификация

Для дискретной формы системы (F, G, C) из пункта 3. 1. провести реализацию системы.

Запишем систему в виде:

Подавая импульс по первому входу, рассчитаем:

Теперь имея экспериментальные данные, сгруппировав их в матрицы H и H₁ можем приступить к их обработки.

Из собственных векторов от () и () построим:

Для проверки идентификации найдем коэффициент передачи системы

Коэффициент передачи, вычисленный по исходным матрицам

Можно сделать вывод о том, что система идентифицирована, верно