Навигация
Метод неопределенных коэффициентов
1.3.5 Метод неопределенных коэффициентов
Этот метод может быть использован для любого числа аргументов. Но так как этот метод достаточно громоздок, то применяется только в тех случаях, когда число аргументов не более 5-6.
В методе неопределенных коэффициентов используются законы универсального и нулевого множеств и законы повторения. В начале все коэффициенты неопределенны (отсюда и название метода).
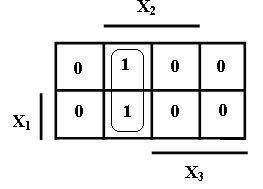
Построим матрицу неопределенных коэффициентов для четырех аргументов. В этом случае мы будем иметь систему из 16-ти уравнений.
Система приведена на следующей странице.
Приравняем все коэффициенты 0 в тех строках, которым соответствует 0 в векторе столбце. Затем приравняем 0 соответствующие коэффициенты в других строках. После этих преобразований система примет следующий вид:
![]() V
V![]() = 1
= 1
![]() V
V ![]() V
V ![]() V
V ![]() V
V ![]() V
V![]() V
V![]() = 1
= 1
![]() V
V ![]() V
V ![]() V
V ![]() V
V ![]() V
V![]() V
V![]() = 1
= 1
![]() V
V ![]() = 1
= 1
![]() V
V ![]() V
V ![]() V
V![]() = 1
= 1
![]() V
V ![]() V
V ![]() V
V ![]() V
V ![]() V
V![]() V
V![]() = 1
= 1
![]() V
V ![]() V
V ![]() V
V ![]() = 1
= 1
![]() V
V ![]() V
V ![]() V
V ![]() V
V![]() V
V![]() = 1
= 1
![]() V
V ![]() V
V![]() V
V![]() = 1
= 1
Теперь в каждой строке необходимо выбрать коэффициент минимального ранга и приравнять его единице, а остальные коэффициенты – 0. После этого вычеркиваем одинаковые строки, оставляя при этом одну из них (те строки, у которых все коэффициенты равны 0, также вычеркиваются).
![]() = 1
= 1
![]() = 1
= 1
![]() = 1
= 1
![]() = 1
= 1
![]() = 1
= 1
Запишем теперь конъюнкции, соответствующие коэффициентам, равным единицам. Мы получим минимальную ДНФ.
F(X1X2X3X4) = X1X3 V X2X3 V X3X4 V X1X2X4 V X1X2X4.
Итак, мы получили несколькими способами минимальную ДНФ, Во всех случаях она получилась одинаковой, то есть любой из описанных методов может быть использован для минимизации функции. Однако эти методы существенно отличаются друг от друга как по принципу нахождения МДНФ, так и по времени исполнения. Для ручных расчетов очень удобен метод карт Карно. Он нагляден, не требует рутинных операций, а выбрать оптимальное расположение правильных прямоугольников не составляет большого труда. В то время как машинная реализация данного метода осложняется необходимостью нахождения оптимального расположения прямоугольников. Естественно применение других методов (метод Квайна, метод Квайна-Маккласки, метод неопределенных коэффициентов) для ручных расчетов нецелесообразно. Они больше подойдут для машинной реализации, так как содержат большое число повторяющихся простых операций.
Задание 2.
2.1 Схема алгоритма для метода Квайна
1. Начало.
2. Ввести матрицу ДСНФ исходной функции.
3. Проверить на склеиваемость i-ю (i=1,m-1: где m – количество строк в ДСНФ) и j-ую (j=i+1, m) строки. Если строки склеиваются, то перейти к пункту 6, в противном случае перейти к пункту 5.
4. Формировать массив простых импликант, предварительно пометив символом ‘*’ ту переменную, по которой данные строки склеиваются.
5. Перейти к пункту 2.
6. Строку, которая не склеилась ни с одной другой строкой записать в конечный массив.
7. Перейти к пункту 2.
8. Вывод полученной матрицы.
9. Конец.
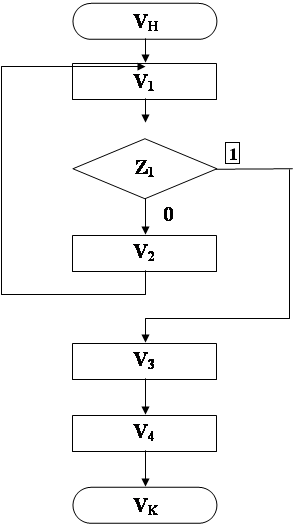
Логическая схема алгоритма в нотации Ляпунова
1 1
VHV1Z1V2¯V3V4VK
VH – начало.
V1 – ввести матрицу ДСНФ исходной функции.
V2 – формировать массив простых импликант, предварительно пометив символом ‘*’ ту переменную, по которой данные строки склеиваются.
V3 – строку, которая не склеилась ни с одной другой строкой записать в конечный массив.
V4 – вывод полученной матрицы.
Z1 – если строки склеиваются, то перейти к пункту 3, в противном случае перейти к пункту 5.
VK – конец.
Граф-схема алгоритма.
Описание машинных процедур
Procedure Stuck(S1, S2: Diz; IndexS1, IndexS2 : byte);
Данная процедура склеивает два, передаваемых ей дизъюнкта. Дизъюнкты задаются в параметрах S1, S2. Индексы IndexS1, IndexS2 определяют индексы этих дизъюнктов в главном рабочем массиве . Алгоритм работы процедуры следующий: сначала ищется количество склеивающихся символов. Если их 0, то они одинаковые, и в конечный массив записывается только один из них. Если 1, то определяется местоположение символа, по которому данные две дизъюнкции склеиваются, и заменяем этот символ на ‘*’. Все полученные результаты заносятся в массив REZ.
Все остальные функции и процедуры программы связаны с действиями над массивами, то есть не имеют непосредственного отношения к данному методу нахождения МДНФ. Поэтому нет смысла их описывать.
2.2 Схема алгоритма для метода Петрика
1. Начало.
2. Ввести матрицу ДСНФ исходной функции и простые импликанты, полученные в методе Квайна.
3. Составить таблицу меток.
4. По таблице меток построить конъюнкцию дизъюнкций, каждая из которых есть совокупность тех импликант, которые в данном столбце имеют метки.
5. Произвести раскрытие скобок в полученном выражении с учетом законов поглощения.
6. Выбрать одну из полученных конъюнкций и представить ее как совокупность соответсвующих простых импликант.
7. Если выбранная комбинация не является минимальной, то перейти к пункту 6, в противном случае перейти к пункту 8.
8. Формировать МДНФ.
9. Вывод полученной матрицы.
10. Конец.
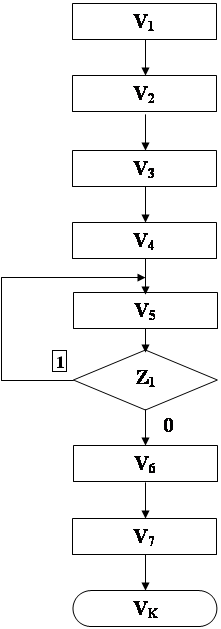
Логическая схема алгоритма в нотации Ляпунова.
1 1
VHV1V2V3V4¯V5Z1V6V7VK
VH – начало.
V1 – ввести матрицу ДСНФ исходной функции и простые импликанты, полученные в методе Квайна.
V2 – составить таблицу меток.
V3 – по таблице меток построить конъюнкцию дизъюнкций, каждая из которых есть совокупность тех импликант, которые в данном столбце имеют метки.
V4 – произвести раскрытие скобок в полученном выражении с учетом законов поглощения.
V5 – выбрать одну из полученных конъюнкций и представить ее как совокупность соответсвующих простых импликант.
Z1 – если выбранная комбинация не является минимальной, то перейти к пункту 6, в противном случае перейти к пункту 8.
V6 – формировать МДНФ.
V7 – вывод полученной матрицы.
VK – конец.
Граф-схема алгоритма.
 | |||
 | |||
Описание машинных процедур
Procedure FormMatrix;
Данная процедура формирует матрицу меток путем попарного анализа дизъюнктов из ДСНФ и матрицы простых импликант. Если стравнение прошло успешно, то соответствующему элементу матрицы меток присваивается значение 1, в противном случае – значение 0.
Function Pokritie(var S: string16): boolean;
Данная функция проверяет, является ли данная комбинация простых импликант полной, то есть накрывает ли она все дизъюнкты матрицы ДСНФ. Это сравнение происходит следующим образом: вводится новый массив – массив соостветсвия столбцам. Каждому элементу нового массива сначала присваивается значение 0. Далее, пробегая все заданные строки матрицы,определяем в каких столбцах стоит 1 и в новом массиве ставим на соответсвующее место 1. Таким образом, если в векторе есть нули, значит данная комбинация дизъюнктов не накрывает полностью все столбцы матрицы. В этом случае функция возвращает значние False, в противном случае функция возвращает значение True.
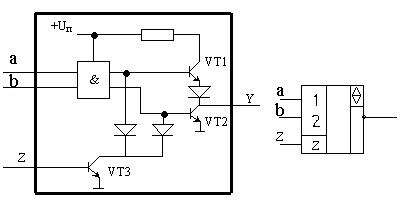
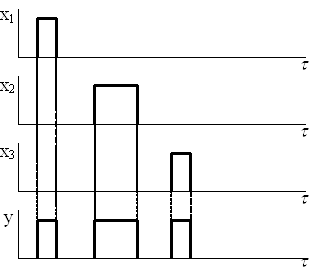
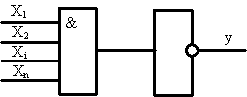
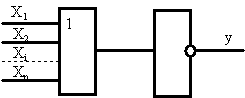
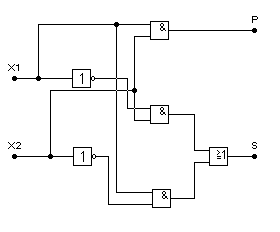
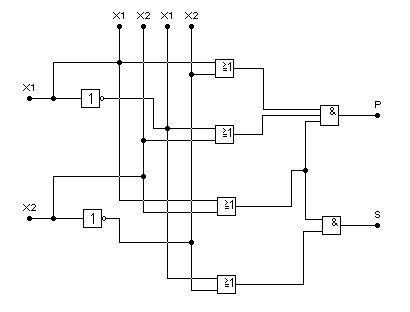
Задание 3. Синтез схемы логического устройства.
Похожие работы
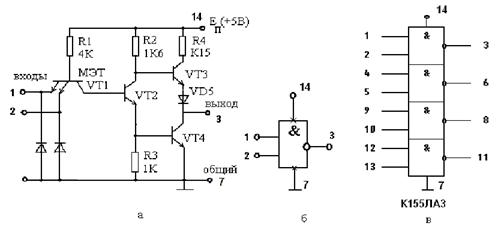
осхемы К155ЛА3 (4 логических элемента 2И-НЕ). Принцип работы ЛЭ И-НЕ ТТЛ Основная особенность микросхем ТТЛ состоит в том, что во входной цепи используется специфический интегральный прибор – многоэмиттерный транзистор (МЭТ), имеющий несколько эмиттеров, объединенных общей базой. Эмиттеры расположены так, что непосредственное взаимодействие между ними через участок базы отсутствует. Поэтому МЭТ ...
... чертеж или схема выполняются в САПР AutoCAD, поэтому наиболее часто используемой вспомогательной программой является конвертор из формата P-CAD в AutoCAD. 1. Основы математического аппарата анализа и синтеза комбинационных логических устройств Все устройства, оперирующие с двоичной информацией, подразделяются на два класса: - комбинационные (дискретные автоматы без памяти). - ...
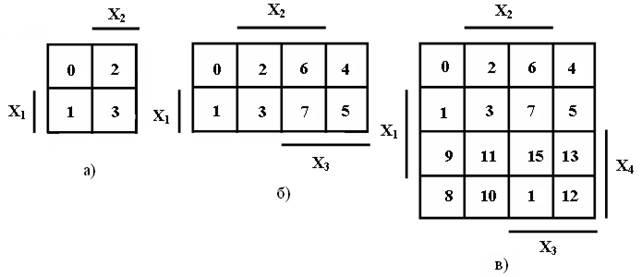
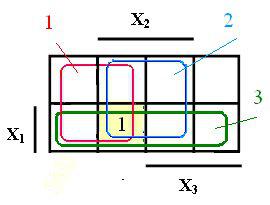
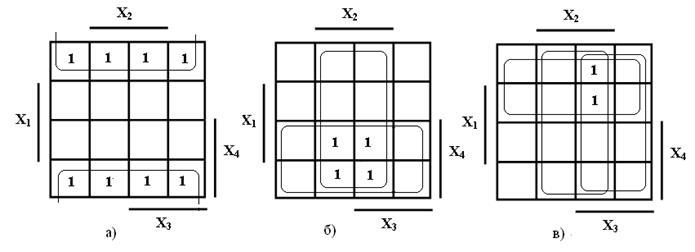
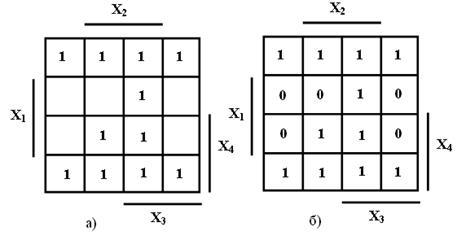
... на рисунке 1 для двух переменных а), трех переменных б) и четырех переменных в). Принципиального значения не имеет, каким вариантом изображения карты Карно пользоваться. В дальнейшем для минимизации используются карты Карно, представленные на рисунке 1 и студентам рекомендуется тоже их использовать. В картах Карно, показанных на рисунке 1, области, где переменные находятся без инверсий (X i), ...
... И-НЕ. Для выполнения этой операции (при имеющемся в окошке булевом выражении) следует “нажать” стрелкой кнопку: 3. Математические модели и эквивалентные схемы в программе логического проектирования Любой реальный логический элемент(ЛЭ) не мгновенно реагирует на изменения входных сигналов, поэтому имеется некоторая паразитная задержка между моментом времени, в который на его входы поступают новые ...
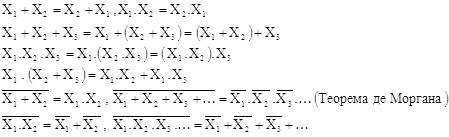
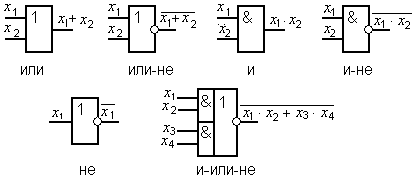
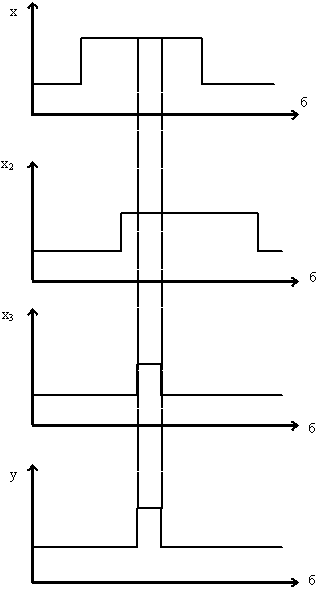
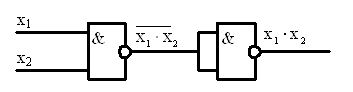
0 комментариев