Навигация
Изменения, влияющие на оптимальность решения
2.2 Изменения, влияющие на оптимальность решения
Текущее оптимальное решение перестает быть оптимальным, если разности ![]() не удовлетворяют условию оптимальности. Используя вектор двойственных цен
не удовлетворяют условию оптимальности. Используя вектор двойственных цен ![]() , запишем
, запишем
![]() .
.
Отсюда следует, что на оптимальность решения влияют только коэффициенты с, целевой функции (и, следовательно, вектор ![]() ) и/или стоимости ресурсов, представленные векторами
) и/или стоимости ресурсов, представленные векторами ![]() . Рассмотрим последовательно каждый фактор, влияющий на оптимальность решения.
. Рассмотрим последовательно каждый фактор, влияющий на оптимальность решения.
Изменение коэффициентов целевой функции. Для определения влияния изменений коэффициентов целевой функции следует пересчитать разности ![]() только для небазисных переменных, поскольку при любых изменениях коэффициентов
только для небазисных переменных, поскольку при любых изменениях коэффициентов ![]() , соответствующих базисным переменным, разности
, соответствующих базисным переменным, разности ![]() всегда остаются равными нулю.
всегда остаются равными нулю.
Вычислительная процедура заключается в следующем.
1. Вычисляется вектор двойственных цен ![]() для нового вектора коэффициентов
для нового вектора коэффициентов ![]() .
.
2. Вычисляются разности ![]() для текущей небазисной переменной
для текущей небазисной переменной ![]() . При этом возможны два варианта.
. При этом возможны два варианта.
a. Если условие оптимальности выполняется, текущее решение остается оптимальным, но значение целевой функции может измениться.
Если условие оптимальности не выполняется, следует применить (прямой) симплекс-метод для получения нового оптимального решения.
Предположим, что фабрика игрушек TOYCO проводит новую ценовую политику относительно своих изделий. В соответствии с этим доход от одной модели поезда, грузовика и легкового автомобиля составляет соответственно ![]() ,
, ![]() и
и ![]() . Получаем новую целевую функцию для этой модели
. Получаем новую целевую функцию для этой модели
Максимизировать
![]() .
.
Поскольку текущее базисное решение ![]() состоит из переменных х2, х3 и х6, имеем
состоит из переменных х2, х3 и х6, имеем ![]() . Вычислим вектор двойственных цен.
. Вычислим вектор двойственных цен.
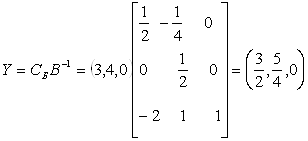 .
.
Разности ![]() для небазисных переменных
для небазисных переменных ![]() ,
, ![]() и
и ![]() вычисляются по формуле
вычисляются по формуле ![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Отметим, что здесь использовалось новое значение коэффициента целевой функции ![]() .
.
Вычисления показывают, что текущее решение ![]() ,
, ![]() и
и ![]() остается оптимальным. Новое значение целевой функции равно
остается оптимальным. Новое значение целевой функции равно
![]() .
.
Предположим, что в рассматриваемой задаче целевая функция имеет следующий вид.
Максимизировать ![]() .
.
Эта функция совпадает с предыдущей целевой функцией, за исключением того, что коэффициент при переменной ![]() теперь равен
теперь равен ![]() . Поэтому необходимо пересчитать только разность
. Поэтому необходимо пересчитать только разность ![]() . В результате получаем следующее.
. В результате получаем следующее.
![]()
Отсюда следует, что переменную ![]() необходимо включить в базисное решение. Имеем следующую симплекс-таблицу.
необходимо включить в базисное решение. Имеем следующую симплекс-таблицу.
Базис ![]()
![]()
![]()
![]()
![]()
![]() Решение
Решение
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Новые значения разностей ![]() для небазисных переменных
для небазисных переменных ![]() ,
, ![]() и
и ![]() в симплекс-таблице выделены. Все остальные элементы таблицы остались такими же, как и в исходной таблице с оптимальным решением. Для нахождения нового оптимального решения следует ввести в базис переменную
в симплекс-таблице выделены. Все остальные элементы таблицы остались такими же, как и в исходной таблице с оптимальным решением. Для нахождения нового оптимального решения следует ввести в базис переменную ![]() и исключить из него переменную
и исключить из него переменную ![]() . В результате получим решение
. В результате получим решение ![]() ,
, ![]() ,
, ![]() и
и ![]()
Кроме того; для исследования влияния коэффициентов целевой функции на оптимальность решения можно также вычислить (по отдельности) интервалы изменения каждого коэффициента, сохраняющие оптимальность текущего решения. Для этого следует заменить текущий коэффициент су выражением ![]() , где
, где ![]() — величина (положительная или отрицательная) изменения коэффициента
— величина (положительная или отрицательная) изменения коэффициента ![]() .
.
Ограничения на величины ![]() можно определить путем вычисления новых разностей
можно определить путем вычисления новых разностей ![]() и наложения на них соответствующего условия оптимальности, которое зависит от того, рассматривается ли задача минимизации или максимизации.
и наложения на них соответствующего условия оптимальности, которое зависит от того, рассматривается ли задача минимизации или максимизации.
Пусть в задаче о фабрике игрушек TOYCO нас интересует интервал допустимости для значения фонда рабочего времени первой операции. Заменим вектор ![]() вектором
вектором
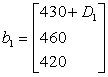 .
.
Переменная ![]() представляет изменения фонда рабочего времени первой операции по сравнению с текущим уровнем в
представляет изменения фонда рабочего времени первой операции по сравнению с текущим уровнем в ![]() минут. Для того чтобы текущее базисное решение осталось недопустимым, необходимо выполнение неравенства
минут. Для того чтобы текущее базисное решение осталось недопустимым, необходимо выполнение неравенства ![]() . Отсюда получаем следующую систему неравенств.
. Отсюда получаем следующую систему неравенств.
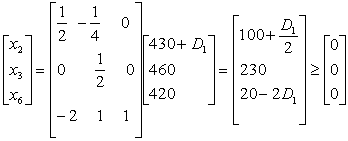 .
.
Первое неравенство ![]() порождает
порождает ![]() , второе неравенство
, второе неравенство ![]() не зависит от
не зависит от ![]() , третье
, третье ![]() дает условие
дает условие ![]() . Таким образом, текущее базисное решение останется допустимым при выполнении неравенств
. Таким образом, текущее базисное решение останется допустимым при выполнении неравенств ![]() . Это эквивалентно следующему интервалу допустимости для фонда рабочего времени первой операции.
. Это эквивалентно следующему интервалу допустимости для фонда рабочего времени первой операции.
![]() Фонд рабочего времени операции
Фонд рабочего времени операции ![]()
или
![]() Фонд рабочего времени операции
Фонд рабочего времени операции ![]()
Изменения значения целевой функции, соответствующее изменение ![]() , равно
, равно ![]() , где
, где ![]() – стоимость (в долларах) одной минуты фонда рабочего времени первой операции (т.е. двойственная цена этого ресурса).
– стоимость (в долларах) одной минуты фонда рабочего времени первой операции (т.е. двойственная цена этого ресурса).
Чтобы проиллюстрировать использование данного интервала допустимости, предположим, что фонд рабочего времени первой операции изменился от ![]() до
до ![]() минут. Текущее базисное решение остается допустимым, поскольку новое значение фонда рабочего времени первой операции принадлежит интервалу допустимости. Для вычисления новых значений переменных воспользуемся значением
минут. Текущее базисное решение остается допустимым, поскольку новое значение фонда рабочего времени первой операции принадлежит интервалу допустимости. Для вычисления новых значений переменных воспользуемся значением ![]() . Далее получим следующее.
. Далее получим следующее.
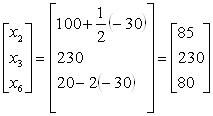 .
.
Для вычисления нового значения целевой функции сначала найдем значения двойственных цен.
 .
.
Таким образом, стоимость одной минуты фонда рабочего времени первой операции равна ![]() . Тогда изменение оптимального дохода составит
. Тогда изменение оптимального дохода составит ![]() . Следует помнить, что данная стоимость минуты фонда рабочего времени первой операции, равная
. Следует помнить, что данная стоимость минуты фонда рабочего времени первой операции, равная ![]() , справедлива только для указанного выше интервала изменения
, справедлива только для указанного выше интервала изменения ![]() . Любое изменение, выходящее за этот интервал, приводит к недопустимому решению. В таком случае следует использовать двойственный симплекс-метод для нахождения нового решения, если оно существует.
. Любое изменение, выходящее за этот интервал, приводит к недопустимому решению. В таком случае следует использовать двойственный симплекс-метод для нахождения нового решения, если оно существует.
Достаточное правило допустимости. Это упрощенное правило можно использовать для проверки того, что одновременные изменения ![]() ,
, ![]() ,
, ![]() ,
, ![]() элементов вектора
элементов вектора ![]() (правых частей неравенств ограничений) сохранят допустимость текущего решения. Предположим, что правая часть
(правых частей неравенств ограничений) сохранят допустимость текущего решения. Предположим, что правая часть ![]()
![]() -го ограничения была изменена на
-го ограничения была изменена на ![]() , причем независимо от изменения правых частей других ограничений, и соответствующий интервал допустимости
, причем независимо от изменения правых частей других ограничений, и соответствующий интервал допустимости ![]() рассчитан так, как показано в примере 4.7-2. Очевидно, что
рассчитан так, как показано в примере 4.7-2. Очевидно, что ![]() , поскольку величина
, поскольку величина ![]() соответствует максимальному уменьшению (возрастанию) значения
соответствует максимальному уменьшению (возрастанию) значения ![]() . Положим
. Положим ![]() равным или отношению
равным или отношению ![]() , или
, или ![]() в зависимости от того, будет ли величина
в зависимости от того, будет ли величина ![]() отрицательной или положительной. По определению
отрицательной или положительной. По определению ![]() . Достаточное правило допустимости гласит, что для данных изменений
. Достаточное правило допустимости гласит, что для данных изменений ![]() ,
, ![]() ,
, ![]() ,
, ![]() достаточным (не необходимым) условием того, что текущее решение останется допустимым, будет выполнение неравенства
достаточным (не необходимым) условием того, что текущее решение останется допустимым, будет выполнение неравенства ![]() . Если это условие не выполняется, то текущее решение может быть как допустимым, так и недопустимым. Сформулированное правило неприменимо, если
. Если это условие не выполняется, то текущее решение может быть как допустимым, так и недопустимым. Сформулированное правило неприменимо, если ![]() выходят из своих интервалов допустимости.
выходят из своих интервалов допустимости.
В действительности достаточное правило допустимости является очень слабым критерием допустимости решения и на практике применяется редко. Даже в том случае, когда допустимость решения может быть подтверждена с помощью этого правила, все равно для получения нового оптимального решении будет, использовано условие допустимости прямого симплекс-метода.
Добавление новых ограничений. Добавление нового ограничения в существующую модель ЛП может привести к одной из следующих ситуаций.
Похожие работы
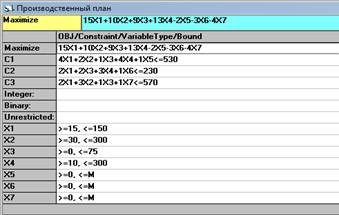
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
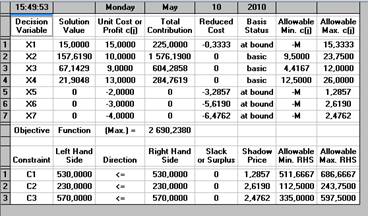
... ведущего столбца равными нулю. Слева от таблицы в q-ой строке запишем переменную хр. Перейти на шаг 1. 1.2 Постоптимальный анализ Постоптимальный анализ (анализ моделей на чувствительность) – это процесс, реализуемый после того, как оптимальное решение задачи получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели. ...
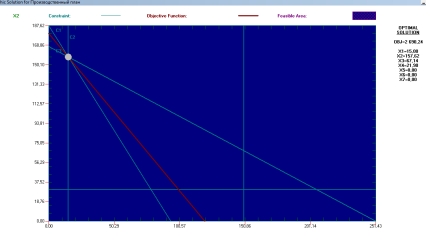
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
... соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке. Выбор каждой последующей экстремальной точки при использовании симплекс-метода определяется следующими двумя правилами. Каждая последующая угловая точка должна быть смежной с предыдущей. Этот переход осуществляется по границам ( ребрам ) пространства решений ...
0 комментариев