Навигация
Новое ограничение является избыточным. Это означает, что новое ограничение выполняется при текущем оптимальном решении
24556
знаков
1
таблица
10
изображений
1. Новое ограничение является избыточным. Это означает, что новое ограничение выполняется при текущем оптимальном решении.
2. Новое ограничение не выполняется при ткущем оптимальном решении. В этом случае необходимо применить двойственный симплекс-метод, чтобы получить (или хотя бы попытаться получить) новое оптимальное решение.
Отметим, что добавление неизбыточного нового ограничения может только ухудшить текущее оптимальное значение целевой функции.
Предположим, что в модели фабрики игрушек TOYCO время выполнения новой четвертой операции составляет соответственно 
, и 
минуту при сборке одной игрушки различных видов. В этом случае четвертое ограничение 
не будет избыточным, и текущее оптимальное решение ему не удовлетворяет. Мы должны ввести новое ограничение в симплекс-таблицу, где представлено текущее оптимальное решение.
Базис 
Решение
Поскольку переменные и являются базисными, из -строки следует исключить соответствующие им коэффициенты (т.е. надо сделать их нулевыми). Для этого надо выполнить следующую операцию.
Новая -строка 
Старая -строка 
(-строка)
(-строка)
В результате получим новую симплекс-таблицу.
Базис Решение
С помощью двойственного симплекс-метода находим новое оптимальное решение 
, 
, 
и 
Похожие работы
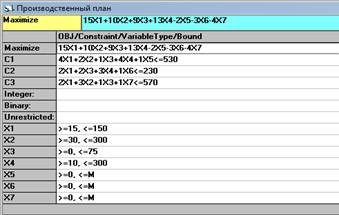
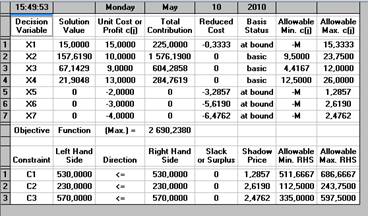
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
... ведущего столбца равными нулю. Слева от таблицы в q-ой строке запишем переменную хр. Перейти на шаг 1. 1.2 Постоптимальный анализ Постоптимальный анализ (анализ моделей на чувствительность) – это процесс, реализуемый после того, как оптимальное решение задачи получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели. ...
... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...
... соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке. Выбор каждой последующей экстремальной точки при использовании симплекс-метода определяется следующими двумя правилами. Каждая последующая угловая точка должна быть смежной с предыдущей. Этот переход осуществляется по границам ( ребрам ) пространства решений ...
0 комментариев