Навигация
Дифференциальные уравнения с запаздывающим аргументом
1. Определения
Дифференциальные уравнения с запаздывающим аргументом вида
![]() (1)
(1)
где ![]() ,
, ![]() ,
, ![]() , называются дифференциальными уравнениями с запаздыванием, зависящим от состояния, а именно с сосредоточенным запаздыванием.
, называются дифференциальными уравнениями с запаздыванием, зависящим от состояния, а именно с сосредоточенным запаздыванием.
Если заданы начальные данные в виде
![]() (2)
(2)
То имеет смысл определить понятие решения, начинающегося в точке σ с функции φ, или, короче, начинающегося в φ.
В дальнейшем будем рассматривать только решения, удовлетворяющие условию Липшица, поэтому следует дать следующее определение:
Def 1.Функция ![]() называется решением системы (1), (2) на отрезке
называется решением системы (1), (2) на отрезке ![]() , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям:
![]()
![]() на отрезке
на отрезке ![]() .
.
Естественно возникает вопрос о существовании и единственности такого решения.
Для начала сделаем некоторые обозначения.
a) ![]()
![]() есть функция, определенная на отрезке
есть функция, определенная на отрезке ![]() и удовлетворяющая условию Липшица с константой L, то есть
и удовлетворяющая условию Липшица с константой L, то есть
![]() ;
;
b) ![]()
c)![]()
Def 2.![]() удовлетворяет условиям a),b),c)}
удовлетворяет условиям a),b),c)}
2. Полезная лемма
Lemma 1: ![]() -выпуклое, замкнутое, ограниченное множество в пространстве непрерывных на отрезке
-выпуклое, замкнутое, ограниченное множество в пространстве непрерывных на отрезке ![]() функций.
функций.
Proof:
1)Выпуклость:
a)Выберем произвольные функции ![]() , тогда
, тогда
![]()
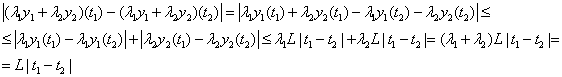
b)![]()
![]() ;
;
c)![]() на отрезке
на отрезке ![]()
![]() на том же отрезке для любых
на том же отрезке для любых ![]() .
.
2)Ограниченность:
Множество ![]() определено так, что все элементы этого множества лежат в шаре радиуса
определено так, что все элементы этого множества лежат в шаре радиуса ![]()
3)Замкнутость:
Возьмем последовательность функций такую, что
![]() ,
, ![]() .
.
a)![]()
Возьмем ![]() тогда
тогда
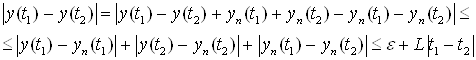
Так как это верно при любом ![]() , то получаем, что предельная функция удовлетворяет условию Липшица с константой L.
, то получаем, что предельная функция удовлетворяет условию Липшица с константой L.
b) По теореме Кантора ![]() равномерно на отрезке.
равномерно на отрезке.
Предположим, что при этом ![]() (для простоты доказательства предположим что
(для простоты доказательства предположим что ![]() , если
, если ![]() , рассуждения проводятся аналогично)
, рассуждения проводятся аналогично)
Возьмем 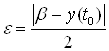 , тогда, так как для любого положительного
, тогда, так как для любого положительного ![]() и любого
и любого ![]() выполнено
выполнено ![]() , то выполнено и для данных
, то выполнено и для данных ![]() и t. Получим:
и t. Получим:
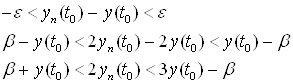
Так как по предположению ![]() , то получаем что
, то получаем что ![]() , а это невозможно, так как
, а это невозможно, так как ![]() . Противоречие показывает, что предельная функция ограничена по норме той же константой
. Противоречие показывает, что предельная функция ограничена по норме той же константой ![]() .
.
c) ![]()
![]()
на отрезке ![]() .
.
Видим, что выполнение условий a,b,c равнозначно тому что ![]() , то есть множество
, то есть множество ![]() замкнуто.
замкнуто.
Лемма доказана полностью.
Похожие работы
... . Но недоверие к символическому исчислению сохранялось до тех пор, пока Джорджи, Бромвич, Карсон, А. М. Эфрос, А. И. Лурье, В. А. Диткин и другие не установили связи операционного исчисления с интегральными преобразованиями. Идея решения дифференциального уравнения операционным методом состоит в том, что от дифференциального уравнения относительно искомой функции-оригинала f(t) переходят к ...
... . Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10). Глава 3. Операционное исчисление § 14. Преобразование Лапласа Понятие оригинала. Кусочно-непрерывная функция называется оригиналом, если выполняются следующие условия: 1) для всех ...
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
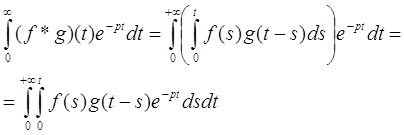
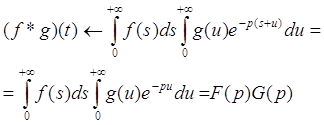
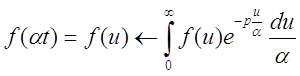
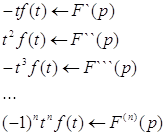





0 комментариев