Проведение эксперимента на объекте исследования
Проверка воспроизводимости эксперимента
Проверка адекватности математического описания
Составление матрицы планирования
Проведение эксперимента на объекте исследования
Проверка воспроизводимости эксперимента
Последовательность выделения наиболее существенных переменных при помощи выборочных ортогональных матриц планирования
Выделение наиболее существенных парных взаимодействий
Навигация
Последовательность выделения наиболее существенных переменных при помощи выборочных ортогональных матриц планирования
Построение моделей статики по методике активного эксперимента
27346
знаков
16
таблиц
5
изображений
2.5 Последовательность выделения наиболее существенных переменных при помощи выборочных ортогональных матриц планирования
Выделение наиболее существенных переменных и их ранжирование можно произвести двумя способами: с помощью вкладов и ортогональных выборочных МП.
Визуальное оценивание показало, что самыми существенными факторами являются 
и 
, имеющие и наибольшие абсолютные величины вкладов, и наибольшее число выделяющихся точек (соответственно восемь и четыре). Построим ВОМП ПФЭ типа 
для этих двух факторов (табл. 2.7), где 
– число факторов в ВОМП, 
– номер строки ВОМП.
Столбцы 
заполняются данными табл. 2.5 следующим образом. Для каждой строки ВОМП выбирается строка в исходной МП, где факторы и имеют такие же знаки. Например, для первой строки табл. 2.7 (
и 
) выбираются строки 1,7,9 и 10 табл. 2.5. Таким образом, в каждой строке ВОМП (табл. 2.7) оказалось по 4 параллельных опыта (
,
,
и 
). Построчные средние значения отклика даны в графе 
.
Таблица 2.7
| z3 | z7 | y1 | y2 | y3 | y4 | Yвыб | S | G | Gтабл |
| -1 | -1 | 209,55 | 158,35 | 189,35 | 210,9 | 192,0375 | 601,5173 | 0,455986 | 0,6841 |
| 1 | -1 | 243,95 | 247 | 265,3 | 255,65 | 252,975 | 92,07083 | ||
| -1 | 1 | 292,5 | 184,45 | 221,9 | 254,9 | 238,4375 | 2127,302 | ||
| 1 | 1 | 301,6 | 262,7 | 262,1 | 353 | 294,85 | 1844,39 |
В графе Sg2выб приведены несмещенные оценки построчных дисперсий, однородность которых проверяется с помощью G-критерия Кохрэна. Расчетное значение критерия G=0,455986, а критическое Gкр=0,6841. Т.к. G<Gкр, можно сделать вывод об однородности оценок дисперсии.Оценки коэффициентов нормированного уравнения регрессии на основании данных ВОМП получились:
â 3=29,3375; â 7=22,0688.
Статистическую значимость оценок коэффициентов проводят по критерию:
âi≤ âiкр=tкр∙S{ âi},
где 
Критическое значение t-критерия Стьюдента выбирают из таблицы для уровня значимости q=0,05 и числа степеней свободы:
nзн=nвос=Nвыб·m(mвыб-1)
Nвыб=4; mвыб=4; m=2
=1166,32
=36,4475
tкр=2,0639
âкр=12,4601
Оценки â 3, â 7 признают статистически значимыми.
Далее исходную табл. 2.5 корректируют по формуле
, (23)
стабилизировав и на уровнях и 
. При этом в тех g-х строках, где 
, из исходных значений отклика вычитают удвоенное значение коэффициента 
, где 
– удвоенное значение 
. Если 
, то вычитание соответствующего 
не производится.
В результате получится скорректированная таблица 2.8.
Таблица 2.8
| g | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | Y | Y' |
| 1 | 1 | 1 | -1 | -1 | 1 | -1 | -1 | -1 | 209,55 | 209,55 |
| 2 | -1 | 1 | -1 | -1 | 1 | 1 | 1 | 1 | 292,5 | 248,3625 |
| 3 | 1 | -1 | -1 | -1 | -1 | -1 | 1 | -1 | 184,45 | 140,3125 |
| 4 | -1 | -1 | 1 | -1 | 1 | 1 | -1 | -1 | 243,95 | 185,275 |
| 5 | -1 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | 158,35 | 158,35 |
| 6 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | -1 | 189,35 | 189,35 |
| 7 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 247 | 188,325 |
| 8 | -1 | 1 | 1 | -1 | 1 | -1 | 1 | -1 | 301,6 | 198,7875 |
| 9 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 265,3 | 206,625 |
| 10 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | 255,65 | 196,975 |
| 11 | -1 | -1 | -1 | -1 | 1 | -1 | 1 | 1 | 221,9 | 177,7625 |
| 12 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | 262,7 | 159,8875 |
| 13 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 | 262,1 | 159,2875 |
| 14 | 1 | -1 | -1 | 1 | 1 | 1 | -1 | 1 | 210,9 | 210,9 |
| 15 | 1 | -1 | 1 | 1 | 1 | 1 | 1 | -1 | 353 | 250,1875 |
| 16 | 1 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | 254,9 | 210,7625 |
По данным этой таблицы (по столбцу y') можно построить новую диаграмму рассеяния (рисунок 2), анализируя которую, выделяют следующие два наиболее существенных фактора. На очередных диаграммах рассеяния ординаты для ранее выделенных наиболее существенных переменных оставляют незаполненными. Отметим, что дисперсия точек на диаграммах рассеяния после выделения наиболее существенных факторов заметно уменьшается по сравнению с первоначальной картиной, поскольку после стабилизации остаются факторы, оказывающие более слабое влияние на величину отклика 
.
Далее аналогичным образом определим следующие два существенных фактора.
Определим медианы на диаграмме рассеяния после стабилизации (рисунок 2).
Рисунок 2
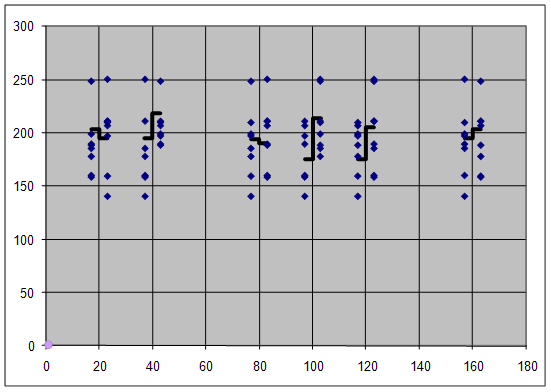
Далее определим вклады и количество выделяющихся точек (таблица2.9).
| вклады | |||||||
| Bz1 | Bz2 | Bz3 | Bz4 | Bz5 | Bz6 | Bz7 | Bz8 |
| -8,1062 | 23,09375 | 0 | -4,3875 | 38,4375 | 30,10625 | 0 | 8,575 |
| выделяющиеся точки | |||||||
| 0 | 0 | 3 | 2 | 5 | 0 | ||
Наиболее существенными факторами являются z5,z6.
Далее строим ВОМП для этих факторов(таблица 2.10).
Таблица 2.10
| z5 | z6 | y1 | y2 | y3 | y4 | Yсред | S | G | Gтабл |
| -1 | -1 | 140,3125 | 206,625 | 196,975 | 159,2875 | 175,8 | 976,8622 | 0,311196 | 0,6841 |
| 1 | -1 | 209,55 | 188,325 | 198,7875 | 154,65 | 187,8281 | 564,3275 | ||
| -1 | 1 | 158,35 | 189,35 | 159,8875 | 210,7625 | 179,5875 | 635,4361 | ||
| 1 | 1 | 248,3625 | 185,275 | 210,9 | 250,1875 | 223,6813 | 983,3819 |
Т.к. G<Gкр, можно сделать вывод об однородности оценок дисперсии.
Получим следующие значения коэффициентов:
â 5=14,0305; â 6=9,91016.
Далее по аналогичным формулам проводится оценка значимости.
Nвыб=4; mвыб=4; m=2
=790,002
=24,6876
tкр=2,0639
âкр=10,2548
Коэффициент â 5 признается незначимым, коэффициент â 2 – значимым.
Похожие работы
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... Замечат. С.: Полемон, Герод Аттик, Аристид, Либаний. Ср. Schmid, "Der Atticismus in seinen Hauptvertretern" (1887-97). 17. Принцип детерминизма в философии. Индетерминизм. Детерминизм (от лат. determino - определяю), философское учение об объективной закономерной взаимосвязи и взаимообусловленности явлений материального и ...
... административно-приказное вмешательство в развитие этой науки. Закономерным стало признание плюрализма точек зрения на предмет социологии и её места в системе социальных и гуманитарных наук. Вопрос о дальнейшем развитии социологии как самостоятельной науки и использовании социологических исследований в решении задач социально-экономического развития страны был поднят до общегосударственного уровня ...
... , а 3 формируется путем умножения построчно колонок 1 и 2. Модель в абсолютных единицах после определения коэффициентов записывается в виде Динамическая идентификация Многие технологические объекты управления, функционирование которых в динамике еще недостаточно изучено, не могут быть описаны аналитически. Для получения их динамических моделей также применяются экспериментальные методы. ...
0 комментариев