Навигация
Средняя арифметическая и условия ее применения
42196
знаков
12
таблиц
0
изображений
2. Средняя арифметическая и условия ее применения
Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака всей совокупности образуется как сумма значений этого признака у ее отдельных единиц.
Средняя арифметическая представляет собой ту величину признака, которую имела бы каждая единица совокупности, если бы общий итог признака был равномерно распределен между всеми единицами совокупности. Используется две формы средней арифметической. Для первичных данных – простая средняя арифметическая 
(4), для вторичных данных – средняя арифметическая взвешенная
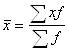(5).
Среднюю арифметическую целесообразно использовать в тех случаях, когда разрыв между минимальным и максимальным значениями признака достаточно невелик (они не отличаются друг от друга в несколько десятков или сотен раз.
Свойства средней арифметической.
1. Произведение средней варианты на сумму частот всегда равно сумме произведения вариант на их частоты
.
2. Если к каждому значению признака вариационного ряда добавить (или отнять) одно и то же число А, то это все равно, что прибавить (или отнять) это число к средней арифметической величине этого ряда
.
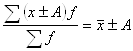3. Если каждый признак ряда умножить (или разделить) на постоянное число А, то это все равно, что умножить (или разделить) на это число среднюю арифметическую величину ряда.
4. Если пропорционально изменить частоты, то средняя от этого не изменится (можно частоты умножить (или делить) на одно и то же число средняя арифметическая от этого не изменится). Это свойство дает возможность частоты заменить удельными весами, называемыми частостями, а также, когда частоты всех вариант одинаковы, вычислять средние по формуле простой средней арифметической. Это свойство важно тогда, когда абсолютные числа – частоты не известны, а известны лишь удельные веса, то есть относительные величины структуры совокупности. Тогда средняя вычисляется так 
, если 
- в процентах или 
, если - в долях единицы.
5. Средняя сумма (разности) двух или нескольких величин равна сумме (разности) их средних.
6. Нулевое свойство средней арифметической. Сумма положительных отклонений от средней арифметической равна сумме отрицательных отклонений от средней арифметической. Сумма всех отклонений индивидуальных значений признака от средней арифметической всегда равна нулю. Именно благодаря этому свойству средняя арифметическая широко применяется в статистике как средство для погашения «сглаживания» случайных отклонений изучаемого признака у отдельных единиц наблюдаемой статистической совокупности.
Пример 4.4
По исходным данным примера 2.1. расчет средней сменной выработки осуществляется по средней арифметической простой:
г.
Применение простой средней арифметической объясняется тем, что объем варьирующего признака для всей совокупности – общее число проработанных лет работниками (61 год) образуется как сумма стажей каждого работника.
Пример 4.5. Расчет среднего производственного стажа работников на основе ряда распределения
| Стаж, г. | Число работников | Середина интервала |
|
| 2-5 5-8 8-11 | 4 5 2 | 3,5 6,5 9,5 | 14,0 32,5 19,0 |
| Итого | 11 | 65,5 |
В данном случае следует воспользоваться формулой средней арифметической взвешенной, поскольку данные вторичные. Интервальные значения признака встречаются не один раз (т.е. повторяются) и эти числа повторений (частоты) не одинаковы.
Конкретными значениями признака, которые должны непосредственно участвовать в расчетах служат середины (центры) интервалов, весами – частоты.
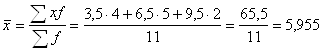
Данный результат отличается от результата, полученного на основе средней арифметической простой. Это объясняется тем, что на основе ряда распределения мы уже не располагаем исходными индивидуальными данными, а вынуждены ограничиться лишь сведениями о величине середины (центра) интервала.
Пример 4.6. Просроченная задолженность по кредитам предприятиями фирмы за отчетный год характеризуется следующими данными:
| № предприятия фирмы | Задолженность по кредитам, тыс. руб. | Удельный вес просроченной задолженности, % |
|
| 1 2 3 | 3500 4000 2000 | 15 30 20 | 52500 120000 40000 |
| Итого | 9500 | 212500 |
Определить средний процент просроченной задолженности фирмы.
Решение: Основой расчета является экономическое содержание показателя.
Удельный вес Объем просроченной задолженности 
просроченной = -------------------------------------------------------- ∙ 100
задолженности, 
, % Объем общей задолженности 
Для расчета среднего процента просроченной задолженности фирмы в этом случае воспользуемся формулой средней арифметической взвешенной:
%.
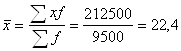Похожие работы
... , во сколько раз одна часть совокупности больше другой, или сколько единиц оДной части приходится на 1, 10, 100, 1000 единиц другой части. Эти относительные величины могут быть исчислены как по абсолютным показателям, так и по показателям структуры. Пример 1.3.7. Имеются следующие данные о численности экономически активного населения РФ по состоянию на конец ноября 2006 г.: Показатели (млн ...
... , средний размер страхового взноса с 1995 по 2003 годы. В работе для анализа статистических данных использован табличный процессор пакет Microsoft Excel. Метод средних величин в изучении общественных явлений. Виды средних величин и их значение в социально-экономических исследованиях. Средняя величина - обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает в ...
ения – отчетность и специально организованное наблюдение. Отчетность – это такая форма наблюдения, при которой предприятия, организации представляют в статистические и вышестоящие органы постоянные сведения, характеризующие их деятельность. Отчетность предоставляется по заранее определенной программе в строго определенные сроки и содержит важнейшие показатели, необходимые в процессе ежедневной ...
... с каждым годом увеличивается, за счет внедрения новых технологий, научного подхода к делу с помощью Иркутской Сельскохозяйственной Академии. 3. Экономико-статистический анализ себестоимости яиц 3.1. Статистическое наблюдение Статистическое наблюдение представляет собой планомерное, научно организованное и, как правило, систематическое собирание данных о явлениях и процессах общественной ...
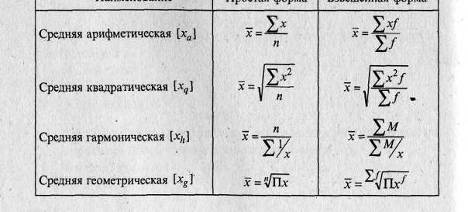
0 комментариев