Навигация
1. Размах вариации
лет
Размах вариации лучше определять по первичным данным, что мы уже делали при расчете величины интервала группировки 
(см. пример 2.1). Для расчета остальных показателей оформим рабочую таблицу
| Стаж, лет | Число работников, чел |
|
|
|
| 2-5 5-8 8-11 | 4 5 2 | 3,5 6,5 9,5 | 14,0 32,5 19,0 | (3,5-5,955)2∙4=24,108 (6,5-5,955)2∙5=1,485 25,134 |
| Итого | 11 | 65,5 | 50,727 |
лет
Дисперсия равна:
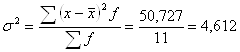
Среднее квадратическое отклонение равно
Коэффициент вариации равен
%
Анализ полученных данных говорит о том, что стаж работников предприятия отличается от среднего стажа 
в среднем на 2,147 года или на 43,3%. Коэффициент вариации превышает 33%, и 40%, следовательно, вариация производственного стажа умеренная, найденный средний стаж плохо представляет всю совокупность работников, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по производственному стажу.
5. Виды дисперсий
Правило сложения дисперсий. Коэффициент детерминации и эмпирическое корреляционное отношение
В статистике важно рассчитывать дисперсии для результативного признака 
, опираясь на данные аналитической группировки.
В этом случае дисперсии примут вид:
- общая дисперсия
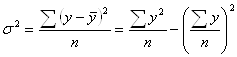(13)
- внутригрупповые дисперсии
(14)
- средняя из внутригрупповых дисперсий
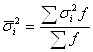(15)
- межгрупповая дисперсия
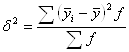(16)
где 
- общая средняя
- средняя 
-ой группы
Правило сложения дисперсий
(17)
На основе этого правила рассчитывают эмпирические показатели тесноты корреляционной связи между факторным и результативным признаками.
Если учесть, что величина межгрупповой дисперсии характеризует влияние только факторного признака, а величина общей дисперсии помимо факторного признака характеризует влияние и всех остальных признаков, то отношение межгрупповой дисперсии к общей покажет силу влияния факторного признака на результативный.
Это отношение называют коэффициентом детерминации 
(18)
Корень квадратный из коэффициента детерминации называют эмпирическим корреляционным отношением.
(19)
Оно показывает степень тесноты связи между факторным и результативным признаком и изменяется в пределах от 0 до 1. Нулевое значение говорит о том, что связи нет (тогда межгрупповая дисперсия равна 0). Значение 1 указывает на наличие функциональной зависимости между признаками, при которой значения исследуемого показателя полностью определяются значениями факторного (группировочного) признака (средняя из внутригрупповых дисперсий в этом случае принимает нулевое значение). И естественно, чем ближе 
к 1, тем связь теснее. Для аналитической характеристики степени связи используют шкалу Чэддока
|
| 0 | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,999 | 1 |
| сила связи | отсутствует | слабая | умеренная | заметная | тесная | весьма тесная | функциональная |
Проиллюстрируем расчеты по данным и результатам расчета примера 2.2.
Пример 4.10. Имеются следующие данные о зависимости выработки работников от их производственного стажа.
| Стаж, г. | Число работников, чел. | Выработка изделий в среднем на работника, шт. |
| 2-5 5-8 8-11 | 4 5 2 | 7,0 8,4 11,0 |
| Итого | 11 |
|
Опираясь на данные представленной таблицы и на исходные данные примера 2.2. определить коэффициент детерминации и эмпирическое корреляционное отношение.
Решение
Вычислим межгрупповую дисперсию по формуле (16)
.
Расчеты произведем в таблице
| Стаж, лет | Число работников, чел. | Средняя выработка |
|
| 2-5 5-8 8-11 | 4 5 2 | 7,0 8,4 11,0 | (7-8,364)2∙4=7,442 (8,4-8,364)2∙5=0,006 (11-8,364)2∙2=13,897 |
| Итого | 11 |
| 21,345 |
Теперь вычислим общую дисперсию выработки изделий на основе индивидуальных данных примера 2.2 по формуле (13)
Для этого вначале возведем данные выработки в квадрат.
| Выработка изделий, шт. |
|
| 1 | 2 |
| 10 7 | 100 49 |
| 7 6 9 8 12 9 8 7 9 | 49 36 81 64 144 81 64 49 81 |
| Итого | 798 |
Тогда 
или 74,9%
=0,865
Величина коэффициента детерминации говорит о том, что вариация выработки изделий на 74,9% зависит от вариации производственного стажа работников и на 25,1% от прочих признаков.
Величина эмпирического корреляционного отношения (0,865) свидетельствует о тесной взаимосвязи между стажем работников и их выработкой.
Похожие работы
... , во сколько раз одна часть совокупности больше другой, или сколько единиц оДной части приходится на 1, 10, 100, 1000 единиц другой части. Эти относительные величины могут быть исчислены как по абсолютным показателям, так и по показателям структуры. Пример 1.3.7. Имеются следующие данные о численности экономически активного населения РФ по состоянию на конец ноября 2006 г.: Показатели (млн ...
... , средний размер страхового взноса с 1995 по 2003 годы. В работе для анализа статистических данных использован табличный процессор пакет Microsoft Excel. Метод средних величин в изучении общественных явлений. Виды средних величин и их значение в социально-экономических исследованиях. Средняя величина - обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает в ...
ения – отчетность и специально организованное наблюдение. Отчетность – это такая форма наблюдения, при которой предприятия, организации представляют в статистические и вышестоящие органы постоянные сведения, характеризующие их деятельность. Отчетность предоставляется по заранее определенной программе в строго определенные сроки и содержит важнейшие показатели, необходимые в процессе ежедневной ...
... с каждым годом увеличивается, за счет внедрения новых технологий, научного подхода к делу с помощью Иркутской Сельскохозяйственной Академии. 3. Экономико-статистический анализ себестоимости яиц 3.1. Статистическое наблюдение Статистическое наблюдение представляет собой планомерное, научно организованное и, как правило, систематическое собирание данных о явлениях и процессах общественной ...
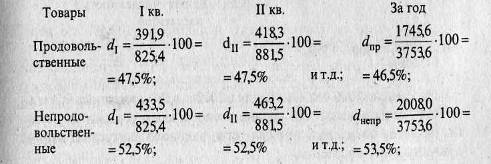
0 комментариев