Навигация
Структурный анализ на уровне групп Ассура
1.1.3 Структурный анализ на уровне групп Ассура
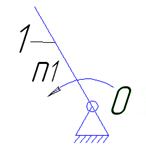
Исходный механизм I (0;1):n=1; р5=1
Определить степень подвижности W=3n-2p
W=3*1-2*1=1
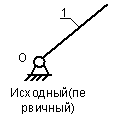
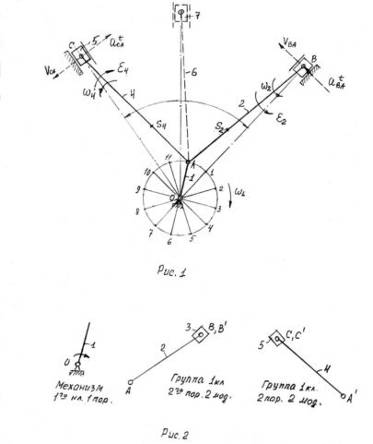
Рисунок 2- Исходный механизм
Вывод: Так как степень подвижности равна 1, следовательно, это исходный механизм.
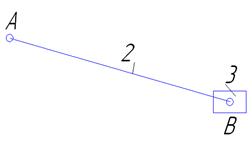
Группа Ассура второго класса, второго вида II2 (2;3): n=2; p5=3.
Определить степень подвижности W=3n-2p
W=3*2-2*3=0
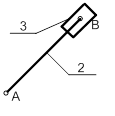
Рисунок 3- Группы Ассура
Вывод: Так как степень подвижности равна 0, следовательно, это группа Асура.![]() Формула механизма: I (0; 1) II2 (2; 3)
Формула механизма: I (0; 1) II2 (2; 3)
Вывод: Механизм является механизмом второго класса, так как наивысший класс группы Ассура равен II.
1.2 Кинематический анализ механизма (лист 1)
Задачи кинематики:
1. Задача положения состоит в определении функции положения;
2. Задача о скоростях, заключается в отыскании аналогов линейных и угловых скоростей;
3. Задача положения, аналога скорости и аналога ускорения центра масс каждого звена;
4. Задача углового положения, аналогов угловой скорости и углового ускорения звеньев;
5. Определение крайних положений механизма и величины хода выходного звена.
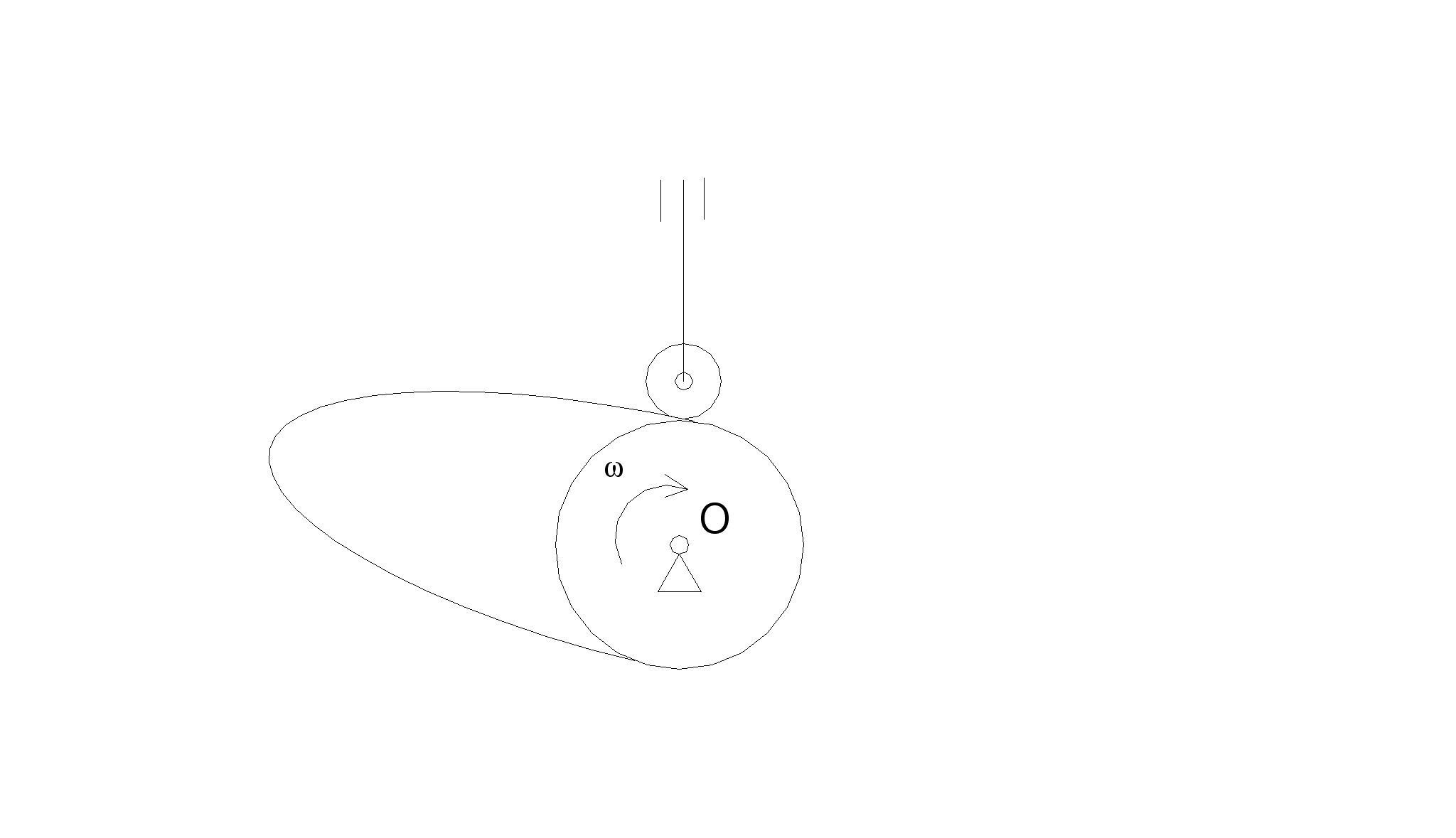
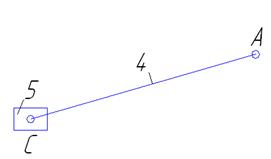
1.2.1 Анализ движения исходного механизма I (0,1)

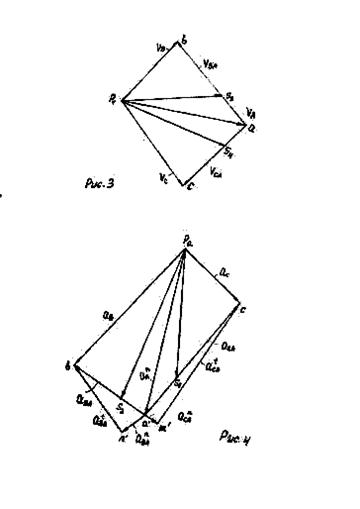
Рисунок 4-Входное звено
Принимаем угол Ψ = 30о
Ψ=30о=0.5235 рад
Cos 30=0.8660 рад
Sin 30=0.5 рад
Допущения:
1 Звенья механизма представляют собой абсолютно твердые тела.
2 Отсутствуют зазоры в кинематических парах.
Для решения задачи пользуемся методом векторных контуров. В этом методе связи в механизме, определяем как характером кинематических пар, так и размерами звеньев, выражаем в форме условий замкнутости векторных контуров, построенных на базе кинематической схемы механизма. В скалярной форме соответствующие зависимости получаем, проектируя контуры на оси координат.
Принимаем угол Ψ = 30о
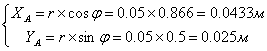 (1)
(1)
Аналоги скорости точки А:
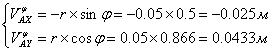 (2)
(2)
Аналоги ускорения точки А:
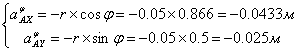 (3)
(3)
1.2.2 Анализ группы Ассура II(2,3)
В данном подразделе определим зависимости ![]() и
и ![]() . Задачу решаем аналитически с использованием метода векторных контуров. Для получения зависимостей составляем векторные контуры. Углы отсчитываем от положительной оси Х против часовой стрелки, а для входного звена в направлении вращения.
. Задачу решаем аналитически с использованием метода векторных контуров. Для получения зависимостей составляем векторные контуры. Углы отсчитываем от положительной оси Х против часовой стрелки, а для входного звена в направлении вращения.
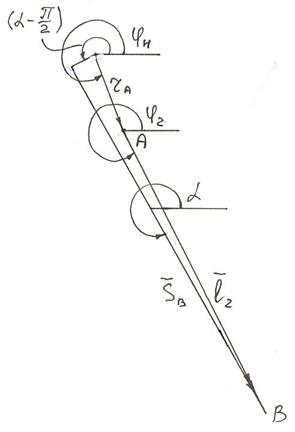
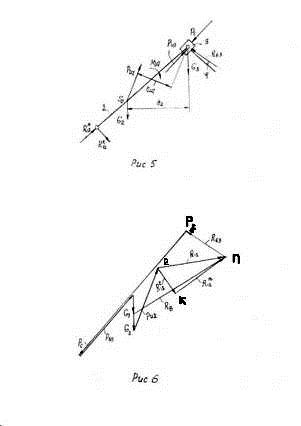
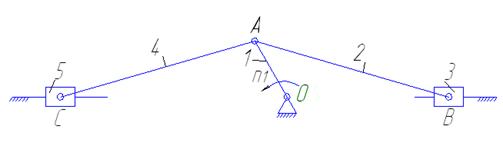
Рисунок 5 – Векторный контур ОАВК
Уравнение замкнутости векторного контура:
![]() (4
(4
Проецируем уравнение на оси системы координат:
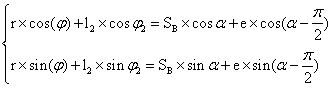 (5
(5
Умножить второе уравнение на ![]() , первое – на
, первое – на ![]() .
.
После вычитания первого уравнения из второго получим:
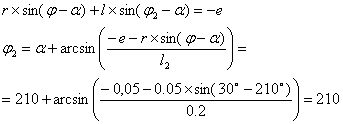 (6
(6
Дифференцируем уравнения исходной системы по обобщенной координате:
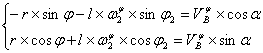 (7)
(7)
После преобразований находим:
- Аналог угловой скорости звена 2:
![]() (8)
(8)
- Аналог скорости точки В:
![]() (9)
(9)
Второй раз дифференцируем ту же систему:
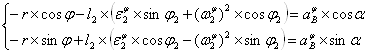
После преобразований получаем:
- Аналог углового ускорения звена 2:
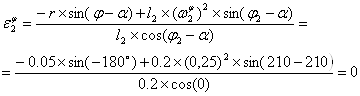 (10)
(10)
- Аналог ускорения точки В:
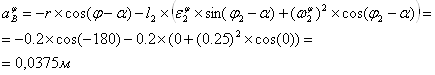
1.2.3 Определяем кинематические функции для центра масс
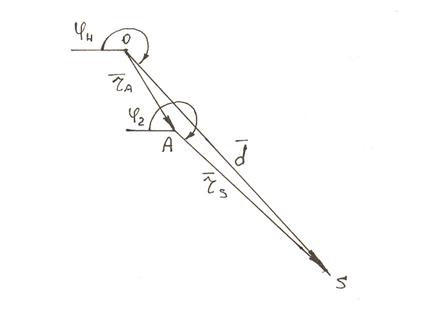
Рисунок 6 – Векторный контур ОАS
Уравнение замкнутости векторного контура:
![]() (11)
(11)
Координаты центра масс звена 2:
 (12)
(12)
Аналог скорости центра масс звена 2:
![]() (13)
(13)
Аналог ускорения центра масс звена 2:
 (14)
(14)
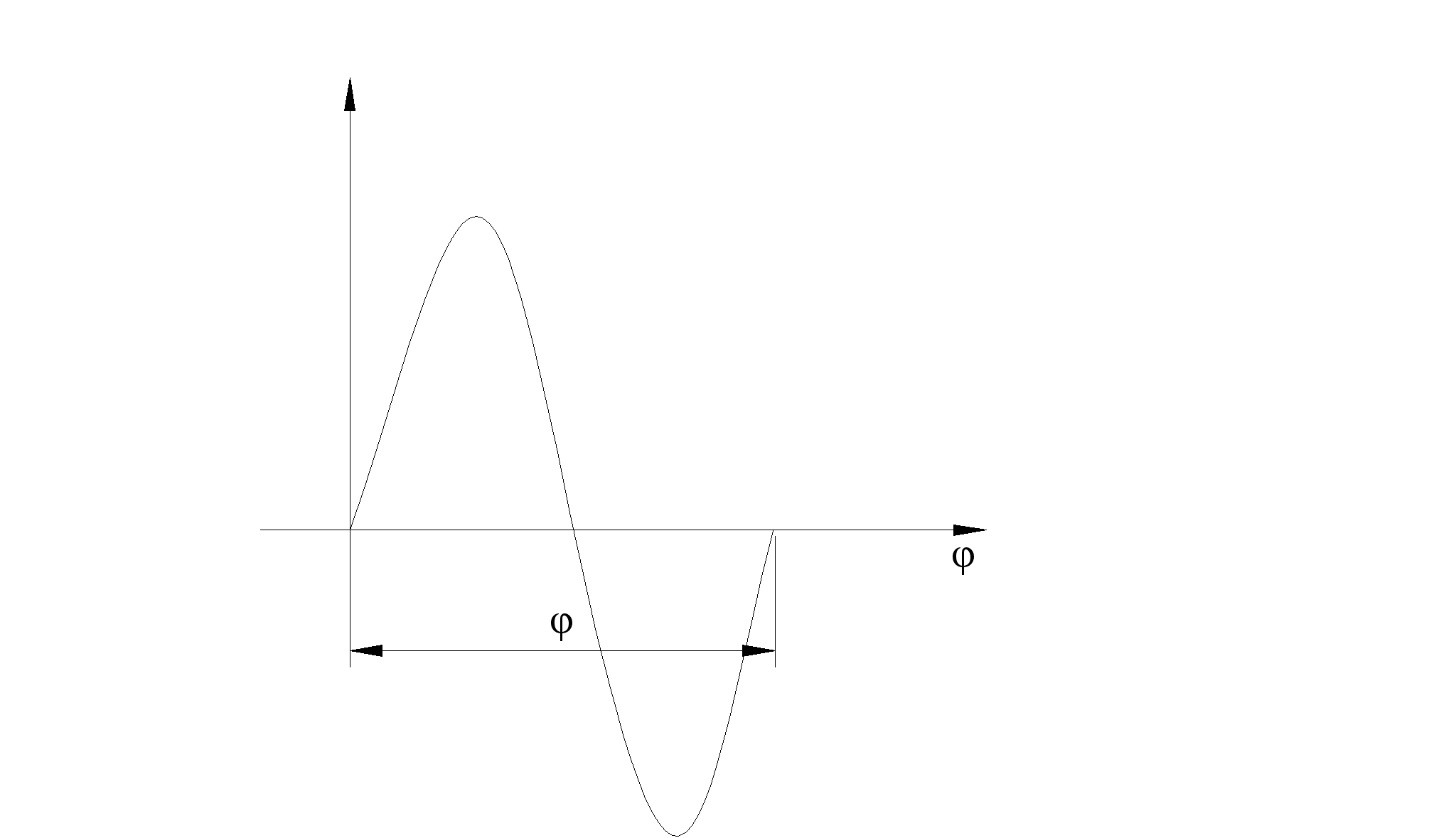
1.2.4 Анализ движения выходного звена
Рабочий ход ползуна – φ max=0.1 рад
Период разгона – от φ =0.524 рад до φ = 3.665 рад
Период замедления – от φ =3.665 рад до φ =0.524 рад
1.2.5 Выбор масштабных коэффициентов
К(l)=0,001 м/мм
K (Sb) =0,001 м/м
K (Vb) =0,001 м/мм
K (Ab) =0,001 м/мм
K (Vs) = 0,001 м/мм
K (As) =0,001 м/мм
1.3 Анализ динамики установившегося движения (лист 2)
Целью динамического анализа является определение закона движения машины по заданным действующим на неё силам.
Основные задачи:
1. построение динамической модели машины;
2. численный анализ параметров динамической модели, угловой скорости и углового ускорения главного вала машины (без маховика );
3. определение работы сопротивлений, величины момента и мощности двигателя;
4. оценка равномерности хода машины, определение момента инерции маховика и значения угловой скорости главного вала в начале цикла;
5. численный анализ угловой скорости и углового ускорения главного вала машины с маховиком.
Допущения:
А) пренебрегаем трением в кинематических парах и вредными сопротивлениями среды;
Б) момент, развиваемый двигателем, считаем постоянным на всем периоде установившегося движения.
Исходные данные:
![]()
![]()
![]()
![]()
![]()
![]()
P1=![]() H P2=
H P2=![]() H P3=
H P3=![]() H H1=
H H1=![]() H2=
H2=![]()
H3=![]()
![]()
Рассмотрим решение прямой задачи динамики машин – определение закона движения машины по заданным действующим на неё силам. На основе анализа периодических колебаний скорости главного вала оценивается неравномерность хода машины. Если коэффициент неравномерности хода превышает допустимую величину δ, то для уменьшения колебаний скорости на главный вал устанавливается маховик.
Похожие работы
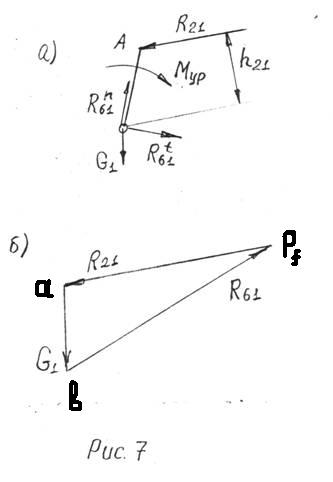
... отрезка "ав". Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скоростей определится из соотношений: . Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении. Как уже говорилось, отрезок плана скоростей ав (вектор) обозначает скорость точки "В" относительно точки ...
... B[44] = 220.000 TETA[44] = 0.0 R[45] = 52.000 B[45] = 220.000 TETA[45] = 0.0 R[46] = 52.000 B[46] = 360.000 TETA[46] = 0.0 6. Силовое исследование рычажного механизма. 6.1 Задачи силового исследования. При силовом исследовании решаются следующие задачи Определение сил действующих на звенья механизма. Определение реакций в кинематических ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
... , - масса маховика, кг - плотность материала, (материал-Сталь 45) - ширина маховика, м - диаметр маховика, м ,м (2,23) где, - коэффициент (0,1÷0,3), м м кг 3. Силовой анализ рычажного механизма 3.1 Построение плана скоростей для расчётного положения Расчётным положением является положение №11. Построение плана скоростей описано в разделе №2. ...
0 комментариев