Навигация
Расчет параметров динамической модели машины
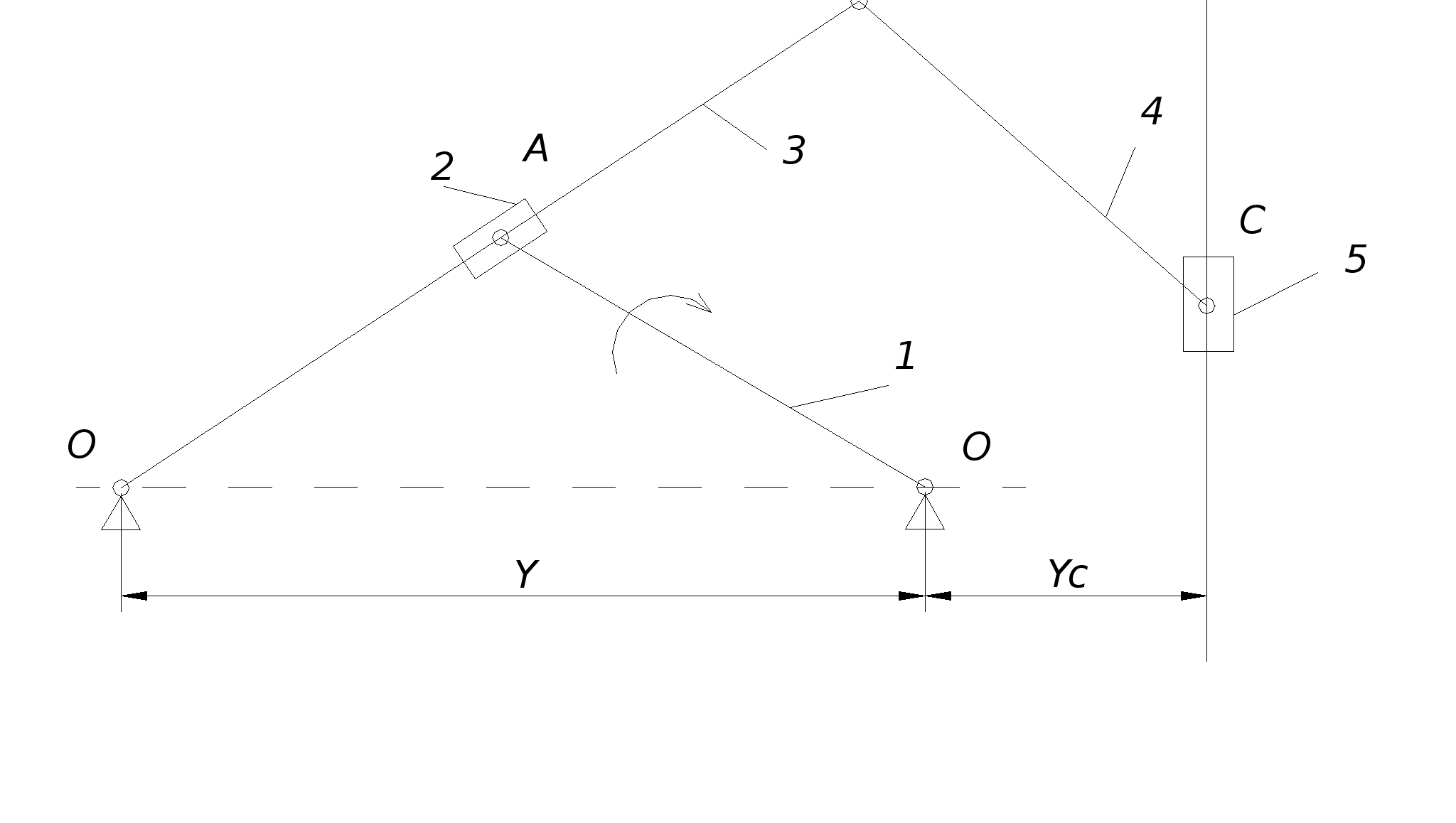
1.3.1 Расчет параметров динамической модели машины
Приведённый момент инерции
![]() (1)
(1)
![]() (2)
(2)
Производная приведенного момента инерции
![]() (3)
(3)
Момент сопротивления
![]() (4)
(4)
Вычисляем параметры динамической модели для положений №1.2,3 и используем полученные данные для получения распечатки «ТММ ДИНАМИКА».
Приведенный момент инерции по формуле (2):
![]() .
.
Производная приведенного момента инерции по формуле (3):
![]()
Момент сопротивления по формуле (4):
![]() ;
;
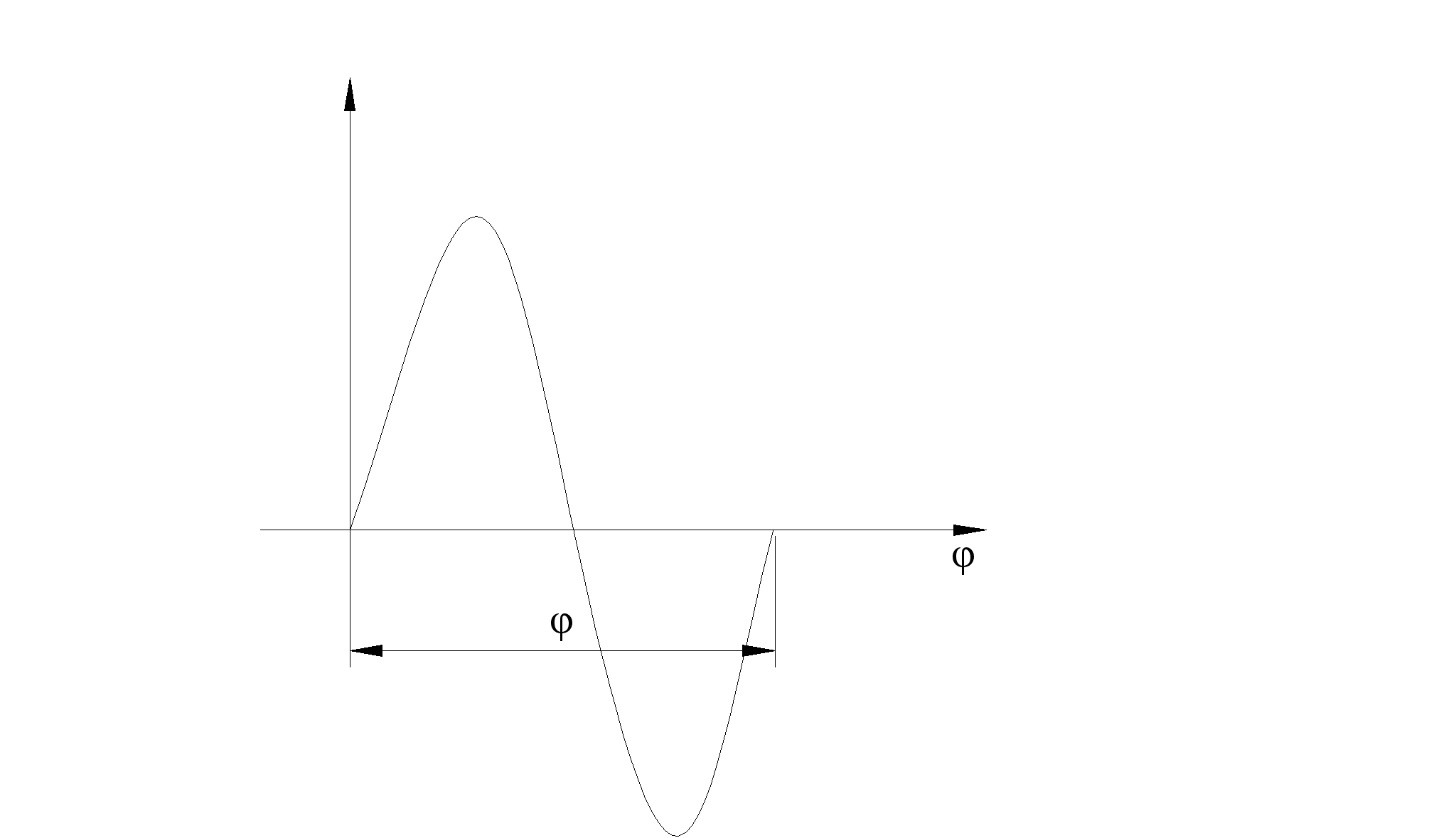
По полученным данным строим диаграммы ![]() ,
,![]()
Методом графического интегрирования строим диаграмму работы сил сопротивления Ас.
Соединив начальную и конечную точки диаграммы, получим движущую работу ![]() . Движущая работа изменяется по линейному закону. Производная от Ад даст значение движущего момента
. Движущая работа изменяется по линейному закону. Производная от Ад даст значение движущего момента ![]()
Масштабный коэффициент графика работ вычисляем по формуле:
![]()
1.3.2 Определение величины движущего момента и мощности
По графику определяем:
![]()
Определяем мощность по формуле:
![]() (5)
(5)
Строим график суммарной работы![]() , ординаты которого равны разности
, ординаты которого равны разности ![]() и
и ![]()
1.3.3 Оценка неравномерности движения
Запишем формулы для ![]() и
и ![]() :
:
 (6)
(6)
![]()
Оставшиеся значения ![]() приведены в распечатке.
приведены в распечатке.
Из выражения (6) выразим ![]() :
:
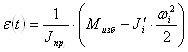 (7)
(7)
![]()
Оставшиеся значения ![]() приведены в распечатке.
приведены в распечатке.
Колебания скорости главного вала машины в режиме установившегося движения будет периодическим. Её амплитуду принято оценивать безразмерным коэффициентом неравномерности хода машины
![]() (8).
(8).
Найдем значения ![]() и
и ![]() из графика угловых скоростей входного звена:
из графика угловых скоростей входного звена:

Подставляя значения ![]() и
и ![]() в формулу (9) определяем неравномерность хода.
в формулу (9) определяем неравномерность хода.
![]()
Неравномерность хода ![]() , так как неравномерность хода по условию задана
, так как неравномерность хода по условию задана ![]() , следовательно, требование не выполнено. Принимаем решение о снижении неравномерности хода путем установки на главном валу машины маховика.
, следовательно, требование не выполнено. Принимаем решение о снижении неравномерности хода путем установки на главном валу машины маховика.
1.3.4 Определение момента инерции маховика
Задача: Определить момент инерции маховика, обеспечивающий заданный коэффициент неравномерности хода машины.
Момент инерции маховика определяем методом Виттенбауэра.
Находим ωmin и ωmax, используя заданные значения ωср и d.
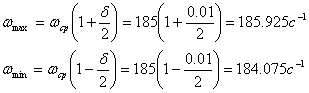 (9)
(9)
Определяем положения механизма φА и φВ, в которых после установки маховика ω = ωmin и ω = ωmax соответственно.
Для решения этой задачи строим диаграмму «энергия – масса» (зависимость ![]() от
от ![]() ). Проводим к графику крайнюю верхнюю и крайнюю нижнюю касательные под углами
). Проводим к графику крайнюю верхнюю и крайнюю нижнюю касательные под углами ![]() и
и ![]() соответственно. Эти углы вычисляем по формулам:
соответственно. Эти углы вычисляем по формулам:
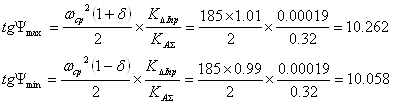 (10)
(10)
Откуда:
![]()
Находим точки касания A и B на диаграмме, проектируем их на оси координат графика и определяем:
![]()
Определяем момент инерции маховика по формуле:
![]() (11)
(11)
Похожие работы
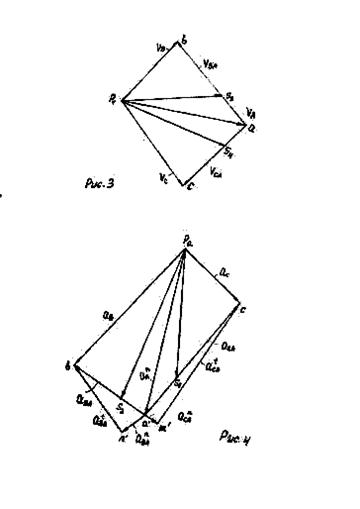
... отрезка "ав". Соединив точки S2 и S4 с полюсом плана скоростей получим векторы скоростей этих точек, а величина скоростей определится из соотношений: . Построенный план скоростей для механизма компрессора позволяет определить угловые скорости звеньев 2 и 4 в их вращательном движении. Как уже говорилось, отрезок плана скоростей ав (вектор) обозначает скорость точки "В" относительно точки ...
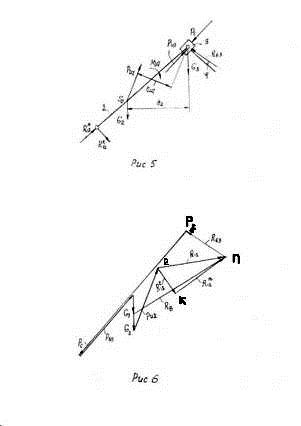
... B[44] = 220.000 TETA[44] = 0.0 R[45] = 52.000 B[45] = 220.000 TETA[45] = 0.0 R[46] = 52.000 B[46] = 360.000 TETA[46] = 0.0 6. Силовое исследование рычажного механизма. 6.1 Задачи силового исследования. При силовом исследовании решаются следующие задачи Определение сил действующих на звенья механизма. Определение реакций в кинематических ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
... , - масса маховика, кг - плотность материала, (материал-Сталь 45) - ширина маховика, м - диаметр маховика, м ,м (2,23) где, - коэффициент (0,1÷0,3), м м кг 3. Силовой анализ рычажного механизма 3.1 Построение плана скоростей для расчётного положения Расчётным положением является положение №11. Построение плана скоростей описано в разделе №2. ...
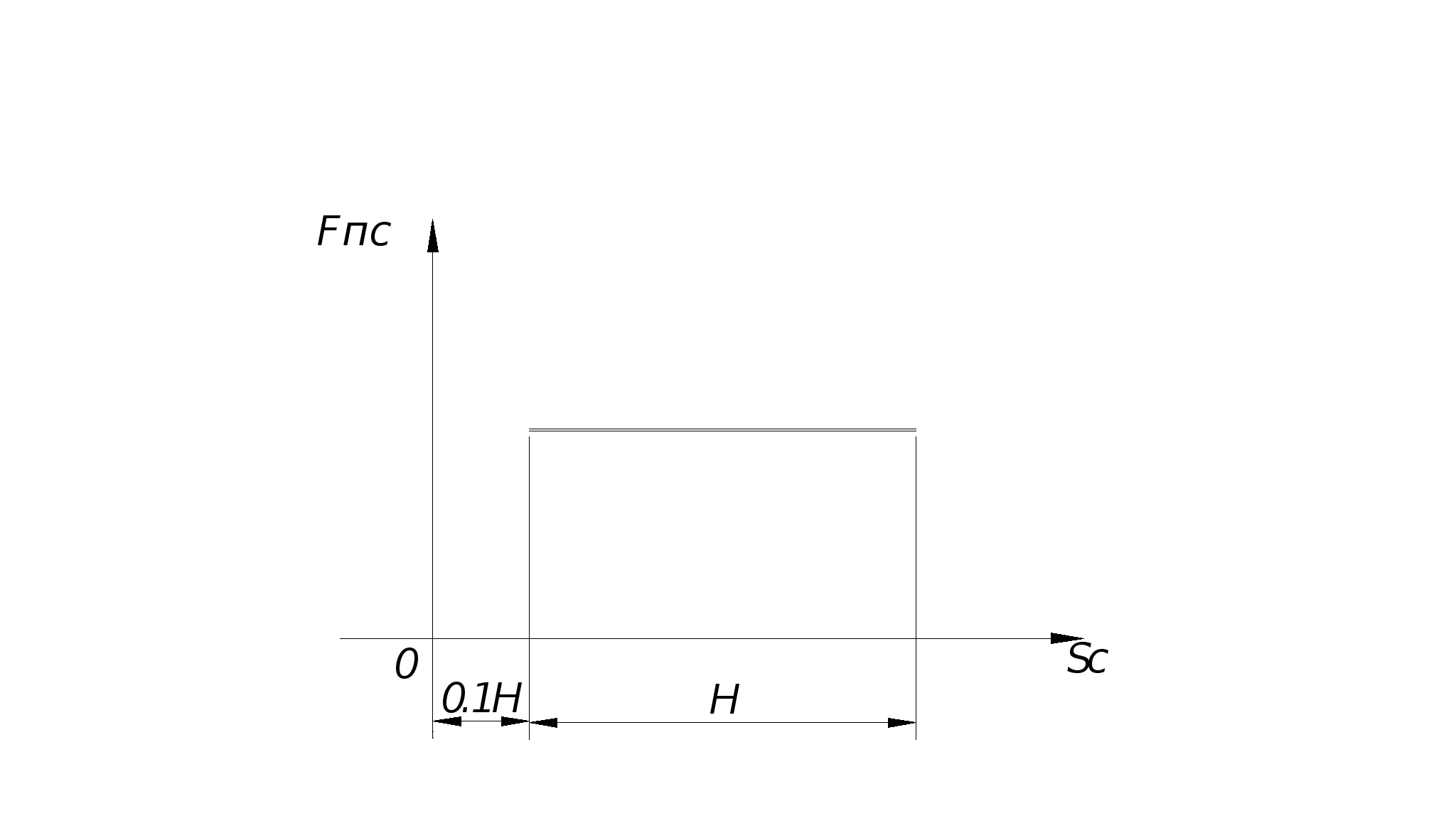
0 комментариев