Навигация
2.5 Схема алгоритма
На рисунке 2.1 представлена схема алгоритма решения задачи №2.
На рисунке 2.2 представлена схема алгоритма ввода исходных данных (подпрограмма-процедура Vvod).
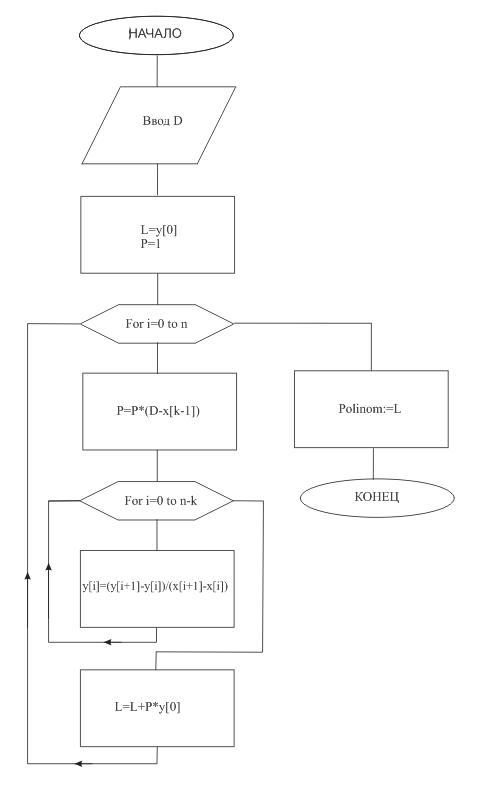
На рисунке 2.3 представлена схема алгоритма интерполяции функции по методу Ньютона с разделенными разностями (newt)
На рисунке 2.4 представлена схема алгоритма записи данных и результата в файл (подпрограмма-процедура zapisb_v_fail).
На рисунке 2.5 представлена схема алгоритма вывода содержимого записанного файла на экран (подпрограмма-процедура outputtoscreen).
2.6 Текст программы
program newton;
uses crt,graph;
const c=10;
type matr=array[0..c,0..c] of real;
mas=array[0..c] of real;
var x,y,koef_polinoma:mas;
a:matr;
b:mas;
d1:real;
n:integer;
fail,fail1,ekran:text;
procedure Vvod(var kolvo:integer; var uzel,fun:mas);
{Процедура осуществляет ввод данных:пользователь вводит с клавиатуры
узлы интерполяции и значения функции в них. Также определяется количество узлов.}
var code,i:integer; s:string;
begin
writeln('введите количество узлов');
readln(kolvo);
kolvo:=kolvo-1;
for i:=0 to kolvo do
begin
repeat
writeln('введите ',i,'-й узел интерполирования');
readln(s);
val(s,uzel[i],code);
until code=0;
repeat
writeln('введите значение функции, соответствующее данному узлу');
readln(s);
val(s,fun[i],code);
until code=0;
end;
end;
procedure newt(var kolvo:integer; D:real; var koef,uzel,fun:mas)
var L,P:real;
begin
L:=fun[0];
P:=1;
for i:=1 to kolvo do
begin
P:=P*(D-uzel[i-1]);
for j:=1 to kolvo-i do
begin
fun[j]:=(fun[j-1]-fun[j])/(uzel[j+i]-uzel[i])
end;
koef[i]:=fun[0];
L:=L+P*fun[0];
end;
end;
procedure newt(var kolvo:integer; D:real; var koef,uzel,fun:mas) {процедура интерполяции функции методом Ньютона}
var L,P:real;
begin
L:=fun[0];
P:=1;
for i:=1 to kolvo do
begin
P:=P*(D-uzel[i-1]);
for j:=1 to kolvo-i do
begin
fun[j]:=(fun[j-1]-fun[j])/(uzel[j+i]-uzel[i])
end;
koef[i]:=fun[0];
L:=L+P*fun[0];
end;
end;
procedure zapisb(koef:mas; uzel,fun:mas; kolvo:integer; var f:text);
{В данной процедуре осуществляется запись в файл данных и результата}
var i:integer;
begin
assign(f,'interpol.txt');
rewrite(f);
for i:=0 to kolvo do writeln(f,'x= ',uzel[i]:8:4,' f(x)=',fun[i]:8:4);
writeln(f,'Интерполяционный полином');
write(f,'p(x)=',koef[0]:8:4);
for i:=1 to kolvo do if i>1 then write (f,'+(',koef[i]:8:4,')*x^',i)
else write (f,'+(',koef[i]:8:4,')*x');
close(f);
end;
procedure vblvod(var f1,f2:text);
{Вывод содержимого записанного файла на экран}
var s1:string;
begin
clrscr;
assign(f1,'interpol.txt');
reset(f1);
assigncrt(f2);
rewrite(f2);
while not eof(f1) do
assigncrt(f2);
rewrite(f2);
while not eof(f1) do
begin
Readln(f1,s1);
writeln(f2,s1);
end;
close(f2);
close(f1);
end;
procedure grafik(kolvo:integer; uzlbl,funktsiya:mas; c:mas);
{Построение графика полученной функции}
var driver,mode,Err,a1,b1,z,i,j:integer; s:string; xt,yt:real;
begin
driver:=detect;
InitGraph(driver,mode,'d:\tp7\bp\bgi');
err:=graphresult;
if err<>grok then writeln('Ошибка при инициализации графического режима')
else
begin
Setcolor(9);
line(320,0,320,480);
line(0,240,640,240);
settextstyle(smallfont,horizdir,3);
setcolor(10);
outtextxy(320,245,'0');
a1:=0;
b1:=480;
z:=-10;
for i:=0 to 20 do
begin
if z<>0 then
begin
str(z,s);
setcolor(10);
outtextxy(a1,245,s);
outtextxy(325,b1,s);
setcolor(8);
line(0,b1,640,b1);
line(a1,0,a1,480);
end;
outtextxy(325,b1,s);
setcolor(8);
line(0,b1,640,b1);
line(a1,0,a1,480);
end;
a1:=a1+32;
b1:=b1-24;
z:=succ(z);
end;
setcolor(5);
for i:=0 to kolvo do
begin
xt:=uzlbl[i];
yt:=funktsiya[i];
putpixel(round(320+xt*32),round(240-yt*24),5);
end;
moveto(round(320+uzlbl[0]*32),round(240-funktsiya[0]*24));
setcolor(11);
for i:=0 to kolvo do
begin
xt:=uzlbl[i];
yt:=0;
for j:=0 to kolvo do yt:=yt+c[j]*vozvedenie_v_stepenb(uzlbl[i],j);
lineto(round(320+xt*32),round(240-yt*24));
moveto(round(320+xt*32),round(240-yt*24));
end;
readln;
closegraph;
end;
end;
{Основная часть программы}
BEGIN
CLRSCR;
Writeln('Программа осуществляет интерполирование функции, заданной в узлах');
Vvod(N,X,Y);
writeln(‘введите значение промежуточной точки’);
readln(d1);
2.7 Тестовый примерwriteln('Нажмите Enter');
readln;
newt(N,d1,X,Y,koef_polinoma);
zapisb(koef_polinoma,x,y,n,fail);
vblvod(fail,fail1);
writeln('Нажмите Enter для просмотра графика функции, затем еще раз для выхода из программы');
readln;
grafik(N,X,Y,koef_polinoma);
END.
readln(d1);
writeln('Нажмите Enter');
readln;
newt(N,d1,X,Y,koef_polinoma);
zapisb(koef_polinoma,x,y,n,fail);
vblvod(fail,fail1);
writeln('Нажмите Enter для просмотра графика функции, затем еще раз для выхода из программы');
readln;
grafik(N,X,Y,koef_polinoma);
END.
Дана табличная функция:
Вычислить разделенные разности 1-го, 2-го, 3-го порядков (n=3) и занести их в диагональную таблицу.
Разделенные разности первого порядка:
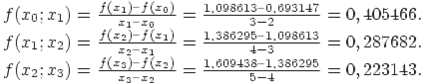
Разделенные разности второго порядка:
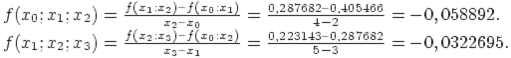
Разделенная разность третьего порядка:
![]()
Интерполяционный многочлен Ньютона для заданной табличной функции имеет вид:
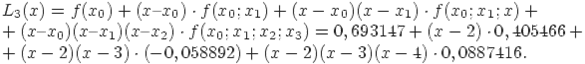
График интерполяционного многочлена будет таким:
procedure zapisb(koef:mas; uzel,fun:mas; kolvo:integer; var f:text);
{В данной процедуре осуществляется запись в файл данных и результата}
var i:integer;
begin
assign(f,'interpol.txt');
rewrite(f);
for i:=0 to kolvo do writeln(f,'x= ',uzel[i]:8:4,' f(x)=',fun[i]:8:4);
writeln(f,'Интерполяционный полином');
write(f,'p(x)=',koef[0]:8:4);
for i:=1 to kolvo do if i>1 then write (f,'+(',koef[i]:8:4,')*x^',i)
else write (f,'+(',koef[i]:8:4,')*x');
close(f);
end;
procedure vblvod(var f1,f2:text);
{Вывод содержимого записанного файла на экран}
var s1:string;
begin
clrscr;
assign(f1,'interpol.txt');
reset(f1);
assigncrt(f2);
rewrite(f2);
while not eof(f1) do
begin
Readln(f1,s1);
writeln(f2,s1);
end;
close(f2);
close(f1);
end;
procedure grafik(kolvo:integer; uzlbl,funktsiya:mas; c:mas);
{Построение графика полученной функции}
var driver,mode,Err,a1,b1,z,i,j:integer; s:string; xt,yt:real;
begin
driver:=detect;
InitGraph(driver,mode,'d:\tp7\bp\bgi');
err:=graphresult;
if err<>grok then writeln('Ошибка при инициализации графического режима')
else
begin
Setcolor(9);
line(320,0,320,480);
line(0,240,640,240);
settextstyle(smallfont,horizdir,3);
setcolor(10);
outtextxy(320,245,'0');
a1:=0;
b1:=480;
z:=-10;
for i:=0 to 20 do
begin
if z<>0 then
Похожие работы
... сформировать более высокий уровень абстракции и обобщения, чем тот, на который ориентировалось традиционное преподавание»[4]. Следовательно, традиционные формы обучения не в состоянии поднять математическое мышление младших школьников на более высокий уровень. Как же решает эту проблему нетрадиционное обучение? Какие свойства математического мышления развивает решение нестандартных задач? Во- ...
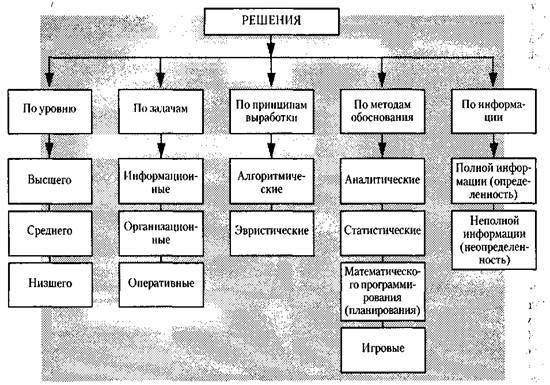
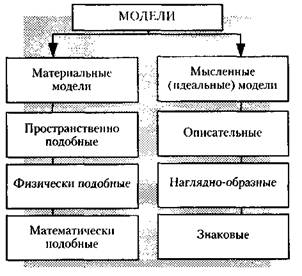
... , которые поддаются математической формализации, моделируя, таким образом, отдельные элементы общего производственного процесса. Конечной целью моделирования производственно-экономической системы является подготовка и принятие руководителем предприятия управленческого решения. Модели производственно-экономических систем можно различать по следующим признакам: – по целям моделирования; – по ...
... Writeln(‘Федеральное агентство по образованию'); GoToXY(22,3); Writeln('Тульский государственный университет'); GoToXY(28,4); Writeln('КАФЕДРА РАДИОЭЛЕКТРОНИКИ'); GoToXY(14,8); Writeln('Интерполяция функции одной переменной методом Ньютона.'); GoToXY(27,9); Writeln('Построение графика полинома.'); GoToXY(34,12); Writeln('Вариант #7'); GoToXY(24,17); Writeln('Студент гр. 220371 ...
сети, построенной на основе различных топологий. Программное обеспечение прикладных систем, предназначенных для профессиональной деятельности руководителя, включает: · системные программные средства; · базовые пакеты прикладных программ; · средства сетевой поддержки компьютеров в локальных и глобальных сетях; · системы прикладного программирования; · тестовые программные средства. ...

0 комментариев