Навигация
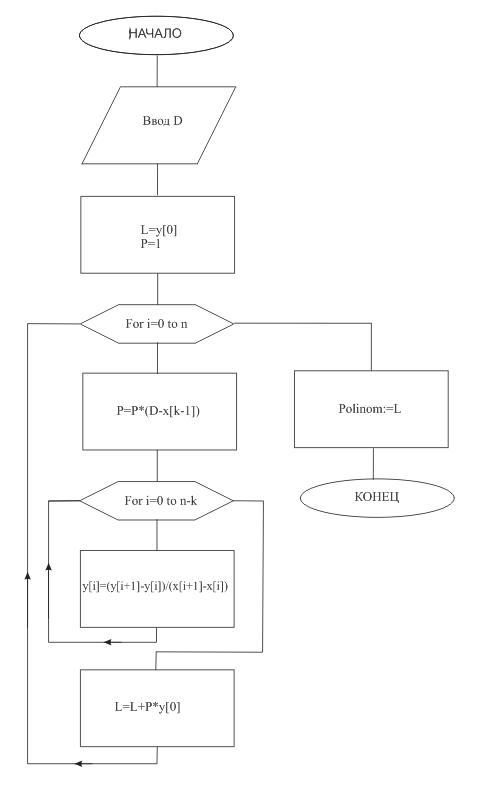
4.5 Схема алгоритма

Рис. 4.1 Основная программа метода

Рис .4.2 Интегрирование методом Гаусса
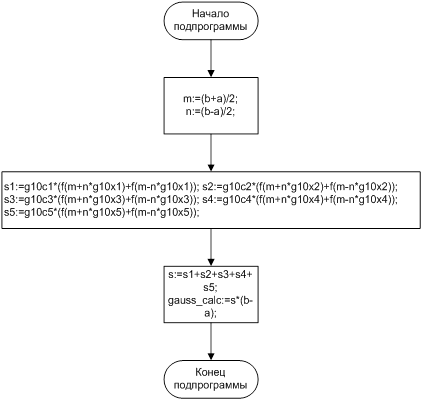
Рис 4.3 Процедура подсчета коэффициентов по методу Гаусса
4.6 Текст программыuses crt,graph;
var aaa,bbb,kkk:real;
const
g10c1=0.9739065285/6.2012983932;
g10c2=0.8650633667/6.2012983932;
g10c3=0.6794095683/6.2012983932;
g10c4=0.4333953941/6.2012983932;
g10c5=0.1488743390/6.2012983932;
g10x1=0.0666713443/6.2012983932;
g10x2=0.1494513492/6.2012983932;
g10x3=0.2190863625/6.2012983932;
g10x4=0.2692667193/6.2012983932;
g10x5=0.2955242247/6.2012983932;
function F(x:real):real;{интегрируемая функция}
begin
F:= ln(1+x*x*x);
end;
function gauss_calc(a,b:real):real; {метод Гаусса}
var n,m,s,s1,s2,s3,s4,s5 :real;
begin
m:=(b+a)/2; n:=(b-a)/2;
s1:=g10c1*(f(m+n*g10x1)+f(m-n*g10x1));
s2:=g10c2*(f(m+n*g10x2)+f(m-n*g10x2));
s3:=g10c3*(f(m+n*g10x3)+f(m-n*g10x3));
s4:=g10c4*(f(m+n*g10x4)+f(m-n*g10x4));
s5:=g10c5*(f(m+n*g10x5)+f(m-n*g10x5));
s:=s1+s2+s3+s4+s5;
gauss_calc:=s*(b-a);
end;
{рекурсивная ф-ция подсчета с заданной точностью}
{ gc - ранее посчитаный интеграл на интервале (a,b)}
function gauss(a,b,eps,gc:real):real;
var t,ga,gb :real;
begin
t:=(a+b)/2; {разбиваем интервал на две половинки}
ga:=gauss_calc(a,t); {в каждой половинке считаем интеграл}
gb:=gauss_calc(t,b);
if abs(ga+gb-gc)>eps then {проверяем точность вычислений}
begin
ga:=gauss(a,t,eps/2,ga); {рекурсия для первой половинки}
gb:=gauss(t,b,eps/2,gb); {рекурсия для второй половинки}
end; {при этом точность повышаем, чтобы }
{при сложении ошибка не накапливалась}
gauss:=ga+gb; {интеграл = сумме интегралов половинок}
end;
procedure inputnum(prm:string;var num:real;lb,ub:real);
var q:boolean;
begin
repeat
write('Введите ',prm,' ');readln(num);
q:=(lb>=num) or (num>ub);
if q then writeln('Число должно быть от ', lb:0:0,' до ',ub:0:0);
until not q;
end;
function main_menu:integer;
var i:integer;
begin
Writeln('==========================================================');
Writeln('0 - выход');
Writeln('1 - решать тестовый пример a=0 b=1.2 k=10 eps = 0.0001');
Writeln('2 - решать пример с произвольными a, b, k, eps');
Writeln('----------------------------------------------------------');
Write('Выбор >>> ');readln(i);
Writeln('==========================================================');
main_menu:=i;
end;
{Вывод графика}
procedure outputgraph(a,b,a1,b1:real;n:integer);
var i,j,j1,k:integer;t,y1,y2,x1,x2,x,y:double;s:string;
begin
clearviewport;
x1:=a1-1;x2:=b1+1;
if x1<0.5 then x1:=-0.5;
y2:=f(ln(bbb/aaa)/(bbb-aaa))*1.2;
y1:=-y2;
{Линия y=0}
setcolor(15);
y:=0;
j:=trunc(480*(y-y2)/(y1-y2));
line(0,j,639,j);
{Линии x=a,x=b}
setcolor(5);
j:=trunc(480*(-y2)/(y1-y2));
i:=trunc(640*(a-x1)/(x2-x1));
j1:=trunc(480*(f(a)-y2)/(y1-y2));
line(i,j,i,j1);
i:=trunc(640*(b-x1)/(x2-x1));
j:=trunc(480*(-y2)/(y1-y2));
j1:=trunc(480*(f(b)-y2)/(y1-y2));
line(i,j,i,j1);
{Сам график}
setcolor(14);
setlinestyle(0,0,3);
t:=(b-a)/n;
k:=0;
j1:=trunc(480*(-y2)/(y1-y2));
for i:=0 to 640 do begin
x:=(x2-x1)*i/640+x1;
y:=f(x);
j:=trunc(480*(y-y2)/(y1-y2));
if j>479 then j:=479;
if j<0 then j:=0;
setcolor(14);
setlinestyle(0,0,3);
if i=0 then moveto(i,j) else lineto(i,j);
setcolor(8);
if (x>t*k+a) then begin
k:=k+1;
setcolor(15);
end;
k:=0;
j1:=trunc(480*(-y2)/(y1-y2));
for i:=0 to 640 do begin
x:=(x2-x1)*i/640+x1;
y:=f(x);
j:=trunc(480*(y-y2)/(y1-y2));
if j>479 then j:=479;
if j<0 then j:=0;
setcolor(14);
setlinestyle(0,0,3);
if i=0 then moveto(i,j) else lineto(i,j);
setcolor(8);
if (x>t*k+a) then begin
k:=k+1;
setcolor(15);
end;
setlinestyle(0,0,1);
if (x>=a) and (x<=b) then line(i,j,i,j1);
end;
setcolor(15);
y:=f(b);
i:=trunc(640*(b-x1)/(x2-x1));
j:=trunc(480*(y-y2)/(y1-y2));
line(i,j,i,j1);
setlinestyle(0,0,1);
setcolor(12);
{Подписи}
setcolor(13);
str(a:6:6,s);
s:='a='+s;
i:=trunc(640*(a-x1)/(x2-x1));
outtextxy(i,j1+2,s);
str(b:6:6,s);
s:='b='+s;
i:=trunc(640*(b-x1)/(x2-x1));
outtextxy(i-10,j1+2,s);
setcolor(15);
y:=0;
j:=trunc(480*(y-y2)/(y1-y2));
outtextxy(5,j+3,'y=0');
readkey;
end;
procedure equateit(eps:real);
var integral,a,b:real;i,j:integer;
begin
a:=0;b:=1;
Integral:=gauss(a,b,eps,gauss_calc(a,b));
writeln('Интеграл = ',integral:0:6);
readkey;
i:=vga;j:=vgahi;
initgraph(i,j,'..\bgi');
outputgraph(a,(b+a)/2,a,b,1);
outputgraph((b+a)/2,b,a,b,1);
outputgraph(a,b,a,b,1);
closegraph;
end;
var sel:integer;
eps:real;
begin
repeat
clrscr;
sel:=main_menu;
case sel of
1:begin
aaa:=0.1;bbb:=1.2;kkk:=10;
eps:=1e-4;
equateit(eps);
end;
2:begin
inputnum('a',aaa,0,1000);
inputnum('b',bbb,-1000,1000);
inputnum('k',kkk,-1000,1000);
inputnum('точность',eps,0.000000001,1);
equateit(eps);
end;
end;
until sel=0;
end.
i:=vga;j:=vgahi;
initgraph(i,j,'..\bgi');
outputgraph(a,(b+a)/2,a,b,1);
outputgraph((b+a)/2,b,a,b,1);
outputgraph(a,b,a,b,1);
closegraph;
end;
var sel:integer;
eps:real;
begin
repeat
clrscr;
sel:=main_menu;
case sel of
1:begin
aaa:=0.1;bbb:=1.2;kkk:=10;
eps:=1e-4;
equateit(eps);
end;
2:begin
inputnum('a',aaa,0,1000);
inputnum('b',bbb,-1000,1000);
inputnum('k',kkk,-1000,1000);
inputnum('точность',eps,0.000000001,1);
equateit(eps);
end;
end;
until sel=0;
end.
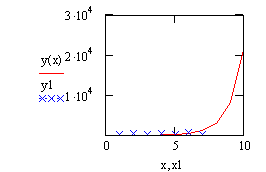
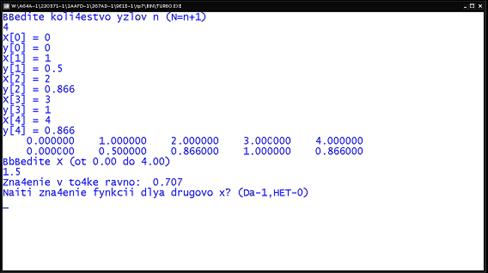
4.7 Тестовый пример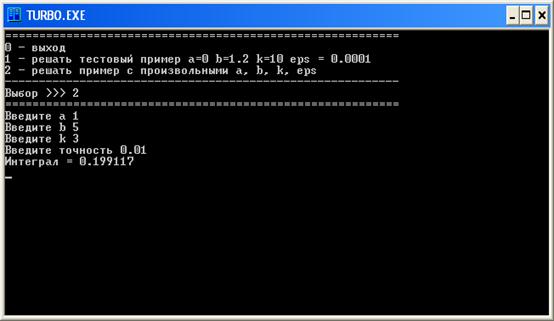
Используя семиточечную формулу вычислить интеграл 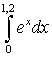 .
.
(Точное решение - 2,3201169227)
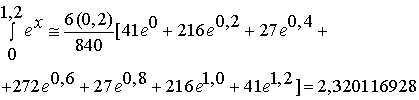
![]()
![]()
![]()
![]()
Заключение
В данной работе описаны и реализованы с помощью блок-схем и языка программирования Turbo Pascal базовые задачи вычислительной математики: решение систем линейных алгебраических уравнений, полиномиальная интерполяция, среднеквадратичное приближение функции, численное интегрирование функций. Представленные методы и реализованные алгоритмы достаточно просты, но в тоже время эффективны для большого количества задач.
Список использованных источников
1. Бахвалов Н., Жидков Н., Кобельков Г. Численные методы. М.: Лаборатория базовых знаний, 2001. 632 с.
2. Вержбицкий В.М., Численных методы. Линейная алгебра и нелинейные уравнения. М.: Высшая школа, 2000. 266 с.
3. Вержбицкий В.М., Основы численных методов. М.: Высшая школа, 2002. 840 с.
4. Пирумов У.Г. Численные методы . М.: Дрофа, 2003. 224 с.
5. Буслов В.А., Яковлев С.Л. Яисленные методы и решение уравнений. Санкт-Петербург, 2001. 44 с.
6. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: Нолидж, 1997. – 616 с.
Похожие работы
... сформировать более высокий уровень абстракции и обобщения, чем тот, на который ориентировалось традиционное преподавание»[4]. Следовательно, традиционные формы обучения не в состоянии поднять математическое мышление младших школьников на более высокий уровень. Как же решает эту проблему нетрадиционное обучение? Какие свойства математического мышления развивает решение нестандартных задач? Во- ...
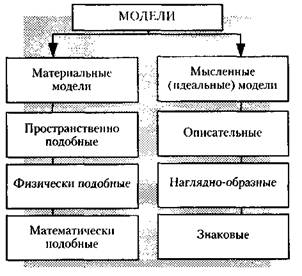
... , которые поддаются математической формализации, моделируя, таким образом, отдельные элементы общего производственного процесса. Конечной целью моделирования производственно-экономической системы является подготовка и принятие руководителем предприятия управленческого решения. Модели производственно-экономических систем можно различать по следующим признакам: – по целям моделирования; – по ...
... Writeln(‘Федеральное агентство по образованию'); GoToXY(22,3); Writeln('Тульский государственный университет'); GoToXY(28,4); Writeln('КАФЕДРА РАДИОЭЛЕКТРОНИКИ'); GoToXY(14,8); Writeln('Интерполяция функции одной переменной методом Ньютона.'); GoToXY(27,9); Writeln('Построение графика полинома.'); GoToXY(34,12); Writeln('Вариант #7'); GoToXY(24,17); Writeln('Студент гр. 220371 ...
сети, построенной на основе различных топологий. Программное обеспечение прикладных систем, предназначенных для профессиональной деятельности руководителя, включает: · системные программные средства; · базовые пакеты прикладных программ; · средства сетевой поддержки компьютеров в локальных и глобальных сетях; · системы прикладного программирования; · тестовые программные средства. ...

0 комментариев