Индексы себестоимости товарной продукции

4.  Индексы себестоимости товарной продукции

Характеристика динамики себестоимости продукции дается при помощи индексов.

Имея данные о себестоимости единицы изделия за предыдущий период (Z₀), по плановым расчетам (Z_пл) и за отчетный период (Z₁), можно дать общую характеристику степени выполнения планового задания по снижению себестоимости и ее динамики с помощью индексов, а также определить абсолютную сумму перерасхода или экономии в результате изменения себестоимости.

При изучении динамики себестоимости по группе предприятий, изготавливающих продукцию одного и того же вида, используется индекс переменного состава, индекс фиксированного состава и индекс влияния структурных сдвигов.¹

На тех предприятиях, на которых изготавливаются разные виды продукции и в общем выпуске преобладает сравнимая продукция, вычисляются показатели снижения себестоимости сравнимой товарной продукции.

К сравнимой относят продукцию, которая производилась в отчетном предыдущем периодах. Основным критерием сравнимости является сохранение продуктом потребительских свойств.

Для оценки выполнения плановых заданий и динамики себестоимости сравнимой товарной продукции используют следующие три индекса.

1.  Индекс планового задания:

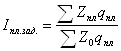
Данный индекс характеризует изменение плановой себестоимости единицы изделия по сравнению со средней годовой себестоимостью предыдущего года в расчете на плановый объем и ассортимент продукции. Разность между числителем и знаменателем дает плановую сумму общей экономии (перерасхода) от изменения себестоимости сравнимой товарной продукции:

2.
Индекс выполнения планового задания

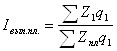
Рассчитывается этот индекс только в аналитических целях и характеризует соотношение уровней фактической и плановой себестоимости в расчете на фактический объем и состав продукции, что устраняет влияние ассортиментных сдвигов. Разность между числителем и знаменателем дает размер сверхплановой суммы экономии (перерасхода), полученной вследствие снижения (повышения) себестоимости продукции:

3.Индекс фактического изменения себестоимости сравнимой товарной продукции:

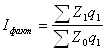
Последний показатель характеризует динамику себестоимости продукции. Поскольку в знаменателе фигурирует фактическая себестоимость единицы продукции предыдущего года, то он охватывает только продукцию, сравнимую с предыдущим годом. Разность между числителем знаменателем дает сумму фактической экономии (перерасхода), полученную вследствие снижения (повышения) себестоимости продукции:

II РАСЧЕТНАЯ ЧАСТЬ

Задание 1. Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности в отчетном году (выборка 20%-ная механическая)

Таблица 2.1

№ предприятия п/п	Выпуск продукции, тыс. ед.	Затраты на производство продукции, млн.руб.	№ предприятия п/п	Выпуск продукции, тыс. ед.	Затраты на производство продукции, млн.руб.
1	160	18,240	16	148	17,612
2	140	17,080	17	110	13,970
3	105	13,440	18	146	17,666
4	150	17,850	19	155	17,980
5	158	18,170	20	169	19,266
6	170	19,210	21	156	17,940
7	152	17,936	22	135	16,335
8	178	19,580	23	122	15,250
9	190	19,440	24	130	15,860
10	164	18,860	25	200	21,000
11	151	17,818	26	125	15,250
12	142	17,040	27	152	17,784
13	120	15,000	28	173	19,030
14	100	13,000	29	115	14,490
150	176	19,360	30	190	19,950

По исходным данным:

1.  Постройте статистический ряд распределения организаций (предприятий) по признаку себестоимость единицы продукции, образовав 5 (пять) групп с равными интервалами.

2.  Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану.

Сделайте выводы по результатам выполнения задания.

РЕШЕНИЕ

Проранжируем в порядке возрастания значение факторного признака:

Х- себестоимость единицы продукции (руб.)

Y- выпуск продукции (тыс.руб)

Таблица 2.2

Себестоимость единицы продукции, руб.Х	Затраты на производство продукции, млн.руб.,	Выпуск продукции, тыс.ед., Y	Себестоимость единицы продукции, руб.Х	Затраты на производство продукции, млн.руб.,	Выпуск продукции, тыс.ед., Y
105	19,950	190	118	17,818	151
105	21,000	200	119	17,612	148
108	19,440	180	119	17,850	150
110	19,580	178	120	17,040	142
110	19,030	173	121	17,666	146
110	19,360	176	121	16,335	135
113	19,210	170	122	17,080	140
114	18,240	160	122	15,250	125
114	19,266	169	122	15,860	130
115	18,860	164	125	15,000	120
115	17,940	156	125	15,250	122
115	18,170	158	126	14,490	115
116	17,980	155	127	13,970	110
117	17,784	152	128	13,440	105
118	17,936	152	130	13,000	100

Для того чтобы произвести группировку, необходимо вычислить величину группировочного интервала по формуле:

где  и  - соответственно max и min значения выпуска продукции,  - число образуемых групп.

 руб

Образуем группы, которые отличаются друг от друга по себестоимости единицы продукции на данную величину (5 руб.).

1 группа будет иметь размеры: 105+5=110 руб.

2 группа: 110+5=115 руб.

3 группа: 115+5=120 руб.

4 группа: 120+5=125 руб.

5 группа: 125+5=130 руб.

Группировку предприятий произведем в рабочей таблице 2.3.

Таблица 2.3 Рабочая таблица с группировкой

Группа	Группы предприятий по величине себестоимости единицы продукции, руб.	Номер предприятия	Себестоимость ед. продукции, руб.
1	105-110	25 30 9	105 105 108
2	110-115	8 15 28 6 20 1	110 110 110 113 114 114
3	115-120	5 10 21 19 27 7 11 4 16	115 115 115 116 117 118 118 119 119
4	120-125	12 18 22 24 26 2	120 121 121 122 122 122
5	125-130	23 13 29 17 3 14	125 125 126 127 128 130

В результате группировки получили следующий ряд распределения (табл. 2.4, 2.5).

Таблица 2.4

Группировка предприятий по себестоимости единицы продукции, руб.
№ группы	Группы предприятий по себестоимости единицы продукции, руб.	Число предприятий по себестоимости единицы продукции		Себестоимость единицы продукции, руб.
		Всего, тыс.ед.	% к итогу	Всего, млн. руб.	% к итогу
А	Б	1	2	3	4
1	105-110	3	10,0	318	9,0
2	110-115	6	20,0	671	19,0
3	115-120	9	30,0	1052	29,8
4	120-125	6	20,0	728	20,6
5	125-130	6	20,0	761	21,6
	Итого:	30	100,0	3530	100,0

Таблица 2.5

Группы	Группы предприятий по величине себестоимости единицы продукции, руб.	Число предприятий	Накопленные частоты
1	105-110	3	3
2	110-115	6	9
3	115-120	9	18
4	120-125	6	24
5	125-130	6	30

Рассчитаем характеристики интервального ряда распределения.

Среднюю рассчитаем по формуле – средняя арифметическая взвешенная.

где - сумма произведений себестоимости единицы продукции на число предприятий,

- общее число предприятий.

Расчет характеристик ряда распределения представим в таблице 2.6.

Таблица 2.6 Расчет характеристик ряда распределения

Группы	Группы предприятий по себестоимости единицы продукции, руб	Число предприятий
1	105-110	3	107,5	322,50	-11	363	3
2	110-115	6	112,5	675,00	-6	216	9
3	115-120	9	117,5	1057,50	-1	9	18
4	120-125	6	122,5	735,00	4	96	24
5	125-130	6	127,5	765,00	9	486	30
Итого:		30		3555,00		1170

 руб

Средняя величина себестоимости единицы продукции предприятий, взвешивая значение признака по абсолютной численности предприятий равна: 118,5 руб.

Дисперсия признака представляет собой средний квадрат отклонения вариантов от их средней величины. Так как у нас имеются сгруппированные данные, то расчеты будем производить по следующей формуле:

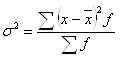; руб

Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности, оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Среднее квадратическое отклонение определяем по формуле:

;  руб

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической.

Коэффициент вариации рассчитаем по формуле:

;  %

Так как коэффициент вариации V=5,27%<33% ,значит наша совокупность количественно однородна.

Построим графики ряда распределения и определим на них моду медиану.

Мода М_о значение случайной величины встречающейся с наибольшей вероятностью.

Моду рассчитаем по формуле:

Модальным будет 3-ий интервал с наибольшей частотой 9.

 руб.

В изучаемой совокупности наиболее часто встречаются предприятия, с величиной себестоимости единицы продукции 118руб.

Для описания моды строим гистограмму:

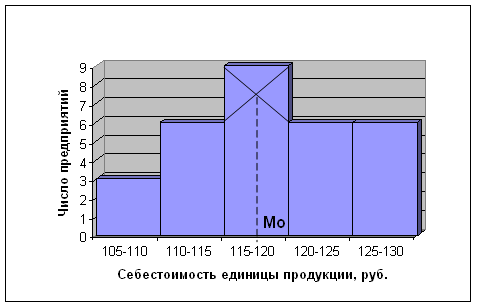
Рис.1 Распределение предприятий по величине себестоимости единицы продукции

Медиана(Ме) - это численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда (построенного в порядке возрастания, либо убывания значения изучаемого признака). Медиану иногда называют серединной вариантой, т.к. она делит совокупность на две равные части.

Для расчета медианы находим накопленные частоты ().

Накопленная частота в 3-ем интервале:

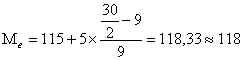 руб

Значит, в изучаемой совокупности 50% предприятий имеют себестоимость единицы продукции менее 118 руб., а остальные 50% имеют себестоимость единицы продукции более 118 руб.

Для описания медианы строим камуляту:

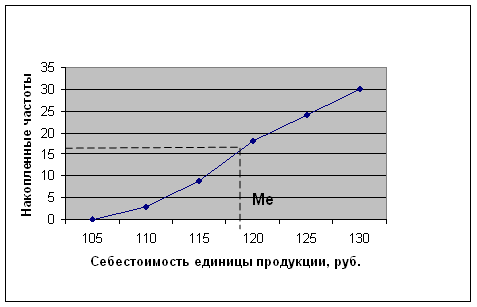
Рис.2 Распределение предприятий по величине себестоимости единицы продукции

Ответ: В результате расчетов получили следующее:

1.  Средний размер себестоимости единицы продукции составляет 118,5руб.

2.  Среднее квадратическое отклонение 6,245руб.

3.  Коэффициент вариации 5,27 %

4.  Наиболее часто встречаются предприятия, с величиной себестоимости единицы продукции на сумму 116руб.

5.  50% предприятий имеют себестоимость единицы продукции менее 117 руб., а остальные 50% имеют себестоимость единицы продукции более 117 руб.(медиана).

Задание 2. По исходным данным:

1.  Установите наличие и характер связи между признаками – выпуск продукции и себестоимость единицы продукции методом аналитической группировки, образовав заданное число групп с равными интервалами по факторному признаку.

РЕШЕНИЕ

Для того чтобы произвести группировку, рассчитаем величину группировочного интервала по формуле:

где  и  - соответственно max и min значения выпуска продукции,  - число образуемых групп.

 тыс.ед

Образуем группы, которые отличаются друг от друга по выпуску продукции на данную величину (20 тыс. ед.).

1 группа будет иметь размеры: 100+20=120 тыс. ед.

2 группа: 120+20=140 тыс. ед.

3 группа: 140+20=160 тыс. ед.

4 группа: 160+20=180 тыс. ед.

5 группа: 180+20=200 тыс. ед.

Группировку предприятий произведем в рабочей таблице 2.7

Таблица 2.7 Рабочая таблица группировок

Группа	Группы предприятий по размеру выпуска продукции тыс.ед.	Номер предприятия	Выпуск продукции, тыс. ед.	Себестоимость единицы продукции, руб.
1	100-120	14 3 17 29	100 105 110 115	130 128 127 126
Всего		4	430,000	511,000
2	120-140	13 23 24 22 26	120 122 130 135 125	125 125 122 121 122
		5	632,000	615,000
3	140-160	2 12 18 16 4 7 11 27 19 21 5	140 142 146 148 150 152 151 152 155 156 158	122 120 121 119 119 118 118 117 116 115 115
		11	1649,000	1300,000
4	160-180	1 10 20 6 28 15 8	160 164 169 170 173 176 178	114 115 114 113 110 110 110
		7	1190,000	786,000
5	180-200	9 30 25	180 190 200	108 105 105
		3	570,000	318,000

На основе данной таблицы составим сводную аналитическую таблицу:

Таблица 2.8 Сводная аналитическая группировка

Группа	Группы предприятий по размеру выпуска продукции, тыс. ед.	Номер предприятий	Выпуск продукции, тыс.ед.		Себестоимость единицы продукции, руб.
			Всего	На 1 предприятие	Всего	На 1 предприятие
А	В	1	2	3	4	5
1	100-120	4	430	107,500	511	127,750
2	120-140	5	632	126,400	615	123,000
3	140-160	11	1649	149,909	1300	118,182
4	160-180	7	1190	170,000	786	112,286
5	180-200	3	570	190,000	318	106,000
	Всего	30	4471	149,033	3530	117,667

Сравнивая графы 3 и5аналитической таблицы видим, что с увеличением выпуска продукции падает себестоимость единицы продукции. Следовательно, между этими показателями имеется обратная зависимость.

Вычислим коэффициент детерминации, который показывает долю вариации результативного признака  под влиянием факторного признака .

Таблица 2.9 Ряд распределения предприятий по размеру выпуска продукции

№ группы	Группы предприятий по размеру выпуска продукции, тыс. ед.	Число предприятий, f	Себестоимость единицы продукции, руб., y	уicр-уср.=уicр-117,667	f*(у-уср)2
1	100-120	4	127,750	10,083	406,6676
2	120-140	5	123,000	5,333	142,2044
3	140-160	11	118,182	0,515	2,917475
4	160-180	7	112,286	-5,381	202,6861
5	180-200	3	106,000	-11,667	408,3567
	Всего	30	117,667		1162,832

Для этого определим межгрупповую дисперсию, характеризующую систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основу группировки.

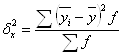
Межгрупповая дисперсия показывает вариацию себестоимости единицы продукции за счет изменения выпуска продукции.

Общую дисперсию, характеризующую вариацию себестоимости единицы продукции под действием всех факторов, рассчитаем по формуле:

Расчет среднего значения признака  представим в таблице 2.10.

Табл. 2.10 Расчет среднего значения признака

№ предприятия	Себестоимость единицы продукции, руб., y	y2
1	105	11025
2	105	11025
3	108	11664
4	110	12100
5	110	12100
6	110	12100
7	113	12769
8	114	12996
9	114	12996
10	115	13225
11	115	13225
12	115	13225
13	116	13456
14	117	13689
15	118	13924
16	118	13924
17	119	14161
18	119	14161
19	120	14400
20	121	14641
21	121	14641
22	122	14884
23	122	14884
24	122	14884
25	125	15625
26	125	15625
27	126	15876
28	127	16129
29	128	16384
30	130	16900
Сумма		416638

Тогда общая дисперсия равна:

 или 91,4 %

Это означает, что на 91,4 % вариация себестоимости единицы продукции обусловлена вариацией выпуска продукции и на 8,6 % – влиянием прочих факторов.

Вычислим эмпирическое корреляционное отношение, которое показывает тесноту связи между группировочным и результативным признаками:

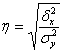
- это свидетельствует о наличие тесной (сильной) связи между выпуском продукции и себестоимость единицы продукции.

Ответ: В результате расчетов получили следующее:

1.  С увеличением выпуска продукции падает себестоимость единицы продукции. Следовательно, между этими показателями имеется обратная зависимость.

2.  Межгрупповая дисперсия 38,761.

3.  Общая дисперсия 42,41.

4.  Коэффициент детерминации 91,4 %.

5.  Эмпирическое корреляционное отношение 0,956.

6.  Связь между себестоимостью единицы продукции и выпуском продукции весьма высокая.

Задание 3. По результатам выполнения задания 1 с вероятностью 0,954 определите

1.  Ошибку выборки среднего уровня себестоимости и границы, в которых будет находиться средний уровень себестоимости продукции в генеральной совокупности.

2.  Ошибку выборки доли предприятий с уровнем себестоимости единицы продукции 125 руб. и более и границы, в которых будет находиться генеральная доля.

РЕШЕНИЕ

Определяем ошибку выборки среднего уровня себестоимости продукции по формуле:

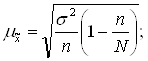 где n=30, k=0.2 или 20%

K=n / N

 руб.

Найдем предельную ошибку:

 

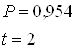
руб

Средний уровень себестоимости единицы продукции будет находиться в следующих границах:

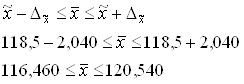
С вероятностью 0,954 можно сказать, что средний уровень себестоимости единицы продукции в генеральной совокупности находится в пределах от 116,460 руб. до 120,540 руб.

2. Определяем ошибку доли предприятий с уровнем себестоимости продукции 125 руб. и более по формуле:

 или 20 %

Среднюю ошибку для выборочной доли определим по формуле:

 или 6,5 %

Ошибка выборки доли предприятий с уровнем себестоимости продукции 125 руб. и более составляет 6,53%

 или 13 %

Найдем пределы, в которых будет находиться генеральная доля, по формуле:

С вероятностью 0,954 можно сказать, что доля предприятий с уровнем себестоимости единицы продукции , равной 125,0 руб. и более будет находится в пределах от 7,0% до 33,0%.

Задание 4. Имеются данные о выпуске однородной продукции и ее себестоимости по двум филиалам фирмы:

Таблица 2.11

Филиал	Базисный период		Отчетный период
	Выпуск продукции, тыс. ед.	Себестоимость единицы продукции, тыс. руб.	Выпуск продукции, тыс. ед.	Себестоимость единицы продукции, тыс. руб.
№ 1	20	2,0	31,5	2,5
№ 2	20	2,1	10,5	2,7

Определите:

1.  Индексы себестоимости единицы продукции в отчетном периоде по сравнению с базисным по каждому филиалу.

2.  Общие индексы себестоимости переменного, постоянного состава, индекс структурных сдвигов.

Результаты расчетов представьте в таблице.

Сделайте выводы.

РЕШЕНИЕ:

1. Найдем индексы себестоимости единицы продукции в отчетном периоде по сравнению с базисным по формуле:

Где i_z- индекс себестоимости единицы продукции;

z₁ - себестоимость единицы продукции в отчетном периоде;

z₀ - себестоимость единицы продукции в базисном периоде.

Филиал № 1

 или 125 %

Филиал № 2:  или 129 %

В первом филиале себестоимость единицы продукции в отчетном периоде по сравнению с базисным увеличилась на 25 %, во втором – на 29 %.