Навигация
Статистические методы изучения экономических явлений
57914
знаков
21
таблица
2
изображения
Введение.
Статистические дисциплины играют важную роль в системе экономического образования. Для общеэкономических специальностей, статистика является основой для разработки и совершенствования методов экономического анализа. Сама же статистика - самостоятельная общественная наука, имеющая свой предмет и метод исследования. Понятие "статистика" происходит от латинского слова "status", которое в переводе, означает - положение, состояние, порядок явлений. Эта наука, изучающая положение дел в государстве. Главная её задача - это сбор цифровых данных, их обобщение и переработка. В зависимости от объекта изучения статистика как наука подразделяется на социальную, демографическую, экономическую, промышленную, торговую, банковскую, финансовую, медицинскую и т.д. Общие свойства статистических данных, независимо от их природы и методы их анализа рассматриваются математической статистикой и общей теорией статистики.
Под предметом статистики понимается количественная сторона массовых общественных явлений в постоянной связи с их содержанием или количественной стороной, а также количественное выражение закономерностей общественного развития в конкретных условиях места и времени. Одной из характерных особенностей статистики является то, что при изучении количественной стороны общественных явлений и процессов она всегда отображает качественные особенности исследуемых явлений, т.е. изучает количество в неразрывной связи, единстве с качеством (качество - это свойства, присущие предмету или явлению, которые отличают данный предмет или явление от других).
Предмет статистики исследуется при помощи определённых понятий, таких как: статистическая совокупность, единица совокупности, признак, статистический показатель, система статистических показателей.
Глава 1. Средние величины и показатели вариации1.1.Средние величины
Средняя величина – это обобщающая количественная характеристика совокупности однотипных явлений по одному варьирующему признаку.
Она отражает объективный уровень, достигнутый в процессе развития явления к определенному моменту или периоду.
Важнейшая особенность средней величины – в том, что она относится к единице изучаемой совокупности и через характеристику единицы характеризует всю совокупность в целом.
Основные свойства средней величины:
Она обладает устойчивостью, что позволяет выявлять закономерности развития явлений. Средняя облегчает сравнение двух совокупностей, обладающих различной численностью.
Она помогает характеризовать развитие уровня явления во времени.
Она помогает выявить и охарактеризовать связь между явлениями.
Средние позволяют исключить влияние индивидуальных значений признака, т.е. они являются абстрактными величинами. Поэтому средние должны употребляться на основе сгруппированных данных.
К расчету средней предъявляются два основных требования:
Среднюю нужно рассчитывать так, чтобы она погашала то, что мешает выявлению характерных черт и закономерностей в развитии явления, а не затушевывала развитие.
Средняя может быть вычислена только для однородной совокупности. Средняя, вычисленная для неоднородной совокупности, называется огульной.
Говоря о методологии исчисления средних, не надо забывать, что средняя всегда дает обобщенную характеристику лишь по одному признаку.
1.2. Виды средних величин.
Средние величины делятся на степенные и структурные.
А) К степенным относятся:
"Средняя арифметическая простая – применяется в случаях, когда известно значение всех показателей по единицам совокупности, при этом данные не сгруппированы. И рассчитывается она по формуле:
=
=
,
где n – число единиц
"В случае, когда данные сгруппированы, имеется информация об индивидуальном значении признака и количестве единиц в каждой группе, используют формулу средней арифметической взвешенной
,
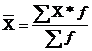где 
- частота повторов,
n – индивидуальное значение признаков.
"Средняя гармоническая взвешенная– применяется в случаях, когда известны индивидуальное значение признака и общий объем явления, а частота повторов индивидуальных значений не задана.
,
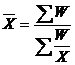где W – общий объём значения;
Х – индивидуальное значение признака.
"Средняя гармоническая простая – используют в ситуациях, когда общий размер явления одинаков для всех индивидуальных значений признака.
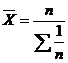
"Средняя хронологическая – применяется в случаях, когда индивидуальное значение признака приводятся на несколько равноценных дат, а рассматривать надо среднюю за период.
,
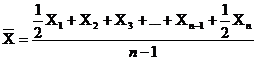где n – число дат;
(n-1) – число периодов
"Средняя геометрическая – применяется в случаях, когда индивидуальное значение признака заданы темпами роста (индексами)
В) Структурные средние
К структурным средним относятся:
мода
медиана
квартиль
дециль
перцентиль
Основные из них – это мода и медиана
Мода
Это значение признака, которое встречается в ряду распределения чаще, чем другие его значения.
В дискретном ряду распределения значения моды определяются визуально. Если же ряд распределения задан как интервальный, то значение моды рассчитывается по следующей формуле:
,
Хо – начальная граница модального интервала,
i – величина модального интервала,
- частота модального интервала,
- частота интервала, предшествующего модальному,
- частота интервала, следующего за модальным.
Медиана
Это центральное значение признака, им обладает центральный член ранжированного ряда. Определение медианы в дискретном ряду производится следующим образом:
Если ряд содержит нечётное число вариантов: медиана – это центральное значение
Если ряд содержит чётное число вариантов: медиана определяется как среднее из двух центральных мест.
Для интервального ряда медиана рассчитывается по следующей формуле:
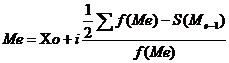
Хо – начальная граница медианного интервала,
i – величина медианного интервала,
- накопленные частоты ряда,
- накопленные частоты интервала, предшествующего медианному
Похожие работы
... при анализе различных явлений, относящихся к одному и тому же объекту. Раздел 2. Методы анализа рядов динамики 2.1 Понятие о статистических рядах динамики Методы анализа рядов динамики занимают немаловажное место в связи с тем, что уровни общественных явлений изменяются во времени и, следовательно, необходимо выделить однородные этапы развития, найти и охарактеризовать свойственные им ...
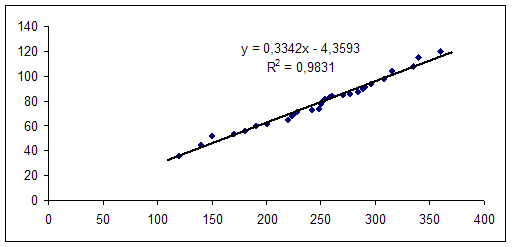
... колеблется в пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем больше влияние оказывает факторный признак на результативный. Для изучения взаимосвязи между производительностью труда и заработной платой проведем дисперсионный анализ на основе результатов проведенной аналитической группировки (смотри таблицу 1) Средний уровень производительности труда по 30 предприятиям составляет ...
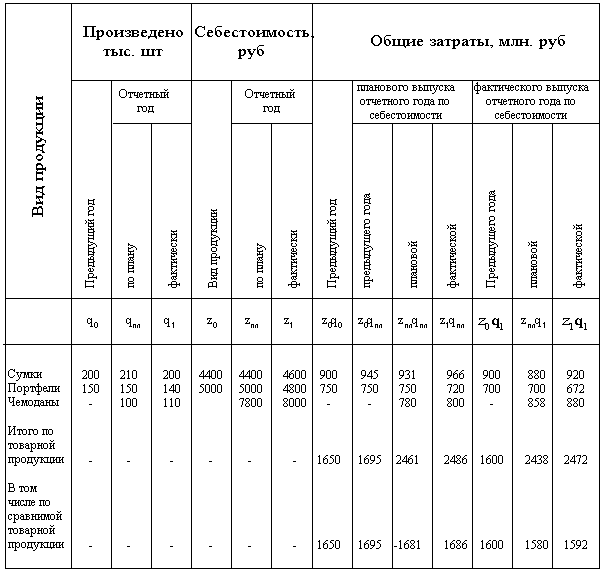
... в сумме 2472-2438=34 млн руб., в том числе по несравнимой продукции: 880-858=22 млн руб. Выпуск и себестоимость продукции на кожгалантерейной фабрике 1.4 Статистические методы изучения уровней динамики Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и ...
... направлено на решение следующих задач: •определение объемов инвестиций, их структуры и темпов изменения; •определение экономической эффективности инвестиций и интенсивности инвестиционной деятельности. Статистическим методом изучения инвестиций является метод группировок. Существует три вида группировок: типологические, структурные и аналитические. Типологическая группировка решает задачу ...
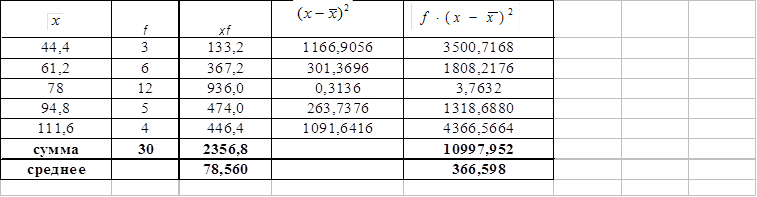
0 комментариев