Знаходимо середину кожного інтервалу

1. Знаходимо середину кожного інтервалу.

Це буде варіаційна ознака, частотою буде кількість робітників, що отримують відповідну заробітну плату. Побудуємо таблицю, в якій зазначимо середини інтервалів.

Місячна ЗРП, X	І цех	II цех	По заводу
104.56	11	2	13
130,76	11	4	15
156,97	2	17	19
183,16	1	7	8
Разом:	25	30	55

2. За формулою середньої зваженої одчислюємо середню ЗРП:

По І цеху:

по II цеху:

по заводу:

2. Модою називається величина ознаки, тобто варіанта, яка найчастіше зустрічається у даній сукупності.

Модою в дискретному ряду розподілу буде варіанта, яка має найбільшу частоту.

Отже, модою тарифного розряду у І цеху буде: Мо1= "3-ій розряд";

II цеху: Мо2="4-ий розряд";

по заводу: Мо3 = "4-ий розряд"

Модою в інтервальному ряду розподілу визначається за залежністю:

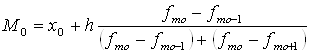 (3)

де х_о та h - відповідно нижня межа та ширина модального інтервалу;

f_mo, f_mо-1 f_mо+1 - частоти модального, перед модального та після модального інтервалу.

Звідси мода заробітної плати дорівнює:

По І цеху:

по II цеху:

по заводу:

3.Медіана - це варіанта, яка знаходиться всередині варіаційного ряду, тобто медіана поділяє ряд розподілу на 2 рівні за чисельністю частини.

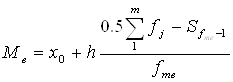 (4)

де х_о та h - відповідно нижня межа та ширина медіанного інтервалу;

f_me - частота медіанного інтервалу;

S_fme-1 - кумулятивна частота передмедіанного інтервалу.

Для того, щоб знайти медіану тарифного розряду, треба спочатку знайти серединну частоту:

 (5)

Далі потрібно накопичувати частоти доти, поки їхня сума не буде перевищувати величину серединної частоти. Потому значенню, на якому ми зупинилися, визначаємо ознаку, а отже, і медіану.

Для знаходження медіани побудуємо допоміжні таблиці.

Для І цеху:

для II цеху:

для заводу: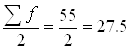

Для І цеху

Розряд	І цех
	чол.	накопичення частот
І	6	6
ІІ	5	11
III	7	19>12,5
IV	4
V	2
VI	1
Разом:	25

Отже, Ме1= "3-ій розряд";

Для II цеху

Розряд	II цех
	чол.	накопичення частот
І	-	-
II	2	2
III	4	6
IV	10	16>15
V	7
Разом:	30

Ме2= "4-ий розряд";

Для заводу

Розряд	Для заводу
	чол.	накопичення частот
І	6	6
II	7	13
III	11	24
IV	14	38>27,5
V	9
Разом:	55

Отже, Ме3= "4-ий розряд"

Медіана заробітної плати визначається за формулою 4.

По І цеху: , тоді медіанний інтервал визначаємо за допомогою накопичення частот:

ЗРП, грн.	І цех
	чол.	накопичення частот
91,46-117,66 117.66-143,86 143,86 - 170,06 170,06- 196,26	11 11 2 1	11 22>12,5
Разом:	25

Отже, інтервал від 117,66 до 143,86 грн.

Тоді

для II цеху:

ЗРП, грн.	II цех
	чол.	накопичення частот
91,46-117,66	2	2
117,66-143,86	4	6
143.86-170,06	17	23>15
170,06-196,26	7
Разом:	30

4. Загальна дисперсія σ² характеризує відхилення індивідуальних значень ознаки сукупності від загальної середньої і розраховується за формулою:

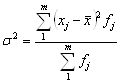 (6)

де m - число одиниць сукупності; х - значення варіант; f - частота;  - середнє арифметичне значення ознаки.

Для того, щоб знайти дисперсно, необхідно:

1). Знайти середню арифметичну кожного ряду розподілу ;

2). Знайти відхилення кожної варіанти від середньої величини: х-; Підносимо кожне відхилення до квадрату: (х-)²;

4).Множимо кожний квадрат відхилення на відповідну частоту: (х-)² * f;

5). Додаємо всі отримані добутки:

6). Ділимо суму отриманих добутків на суму частот:

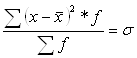
отримаємо показник дисперсії.

Знайдемо дисперсію по тарифному розряду.

І цех:

№ розряду (х)	К-сть працівників (f)	X*f	х-	(х-)2	(х-)2 * f
1	6	6	-1,76	3,0976	18,5856
2	5	10	-0,76	0,5776	2,888
3	7	21	0,24	0,0576	0,4032
4	4	16	1,24	1,5376	6,1504
5	2	10	2,24	5,0176	10,0352
6	1	6	3,24	10,4976	10,4976
Разом	25	69	X	X	48,56

1.

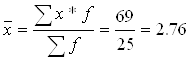
2

II цех

№ розряду (х)	К-сть працівників(f)	X*f	х-	(х-)2	(х-)2 * f
1	-	-	-	-	-
2	2	4	-2,43	5,9049	11,8098
3	4	12	-1,43	2,0449	8,1796
4	10	40	-0,43	0,1849	1,849
5	7	35	0,57	0,3249	2,2743
6	7	42	1,57	2,4649	17,2543
Разом	30	133	X	X	41,367

1.

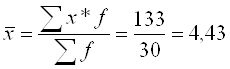
2.

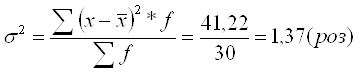
По заводу

№ розряду (х)	К-сть працівників (f)	X*f	х-	(х-)2	(х-)2 * f
1	6	6	-2,67	7,1289	42,7734
2	7	14	-1,67	2,7889	19,5223
3	11	33	-0,67	0,4489	4,9379
4	14	56	0,33	0,1089	1,5246
5	9	45	45	1,7689	15,9201
6	8	48	2,33	5,4289	43,4312
Разом	55	202	X	X	128,1095

1.

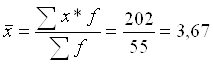
2.

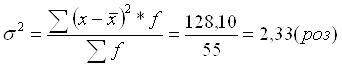
Дисперсія по заробітній платі

По І цеху:

Серед. інтервалу (X)	К-сть працівників (f)	X*f	х-	(х-)2	(х-)2 * f
104,56	11	1150,16	-18,84	354,9456	3904,402
130,76	11	1438,36	7,36	54,1696	595,8656
156,96	2	313,92	33,56	1126,274	2252,547
183,16	1	183,16	59,76	3571,258	3571,258
Разом	25	3085,6	X	X	10324,07

1.

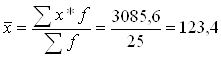
2.

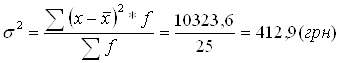
По II цеху

Серед. інтервалу (X)	К-сть працівників (f)	X*f	х-	(х-)2	(х-)2 * f
104,56	2	209,12	-51,44	2646,074	5292,147
130,76	4	523,04	-25,24	637,0576	2548,23
156,96	17	2668,32	0,96	0,9216	15,6672
183,16	7	1282,12	27,16	737,6656	5163,659
Разом	30	4682,6	X	X	13019,7

1.

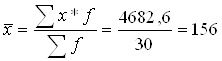
2.

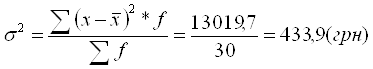
По заводу

Серед, інтервал (X)	К-сть працівників (f)	X*f	х-	(х-)2	(х-)2 * f
104,56	13	1359,28	-36,68	1345,422	17490,49
130,76	15	1961,4	-10,48	109,8304	1647,456
156,96	19	2982,24	15,72	247,1184	4695,25
183,16	8	1465,28	41,92	1757,286	14058,29
Разом	55	7768,2	X	X	37891,49

1.

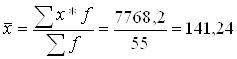
2.

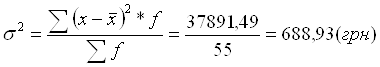
5. Відносною мірою варіації є коефіцієнт варіації. Він дозволяє порівнювати ступінь варіації ознаки у варіаційних рядах, які мають різний рівень середніх величин. Обчислюються як відношення середнього квадратичного відхилення до середнього значення ознаки. В свою чергу середнє квадратичне відхилення обчислюється, як корінь квадратний з дисперсії.

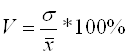 (7)

 (8)

По заробітній платі

Iцех:

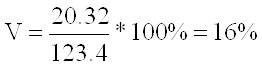 (отже сукупність якісно однорідна);

IIцех:

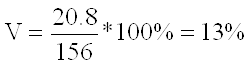 (отже сукупність якісно однорідна);

По заводу:

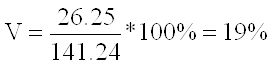(отже сукупність якісно однорідна);

По тарифному розряду

Iцех:

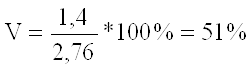 (отже сукупність якісно неоднорідна);

IIцех:

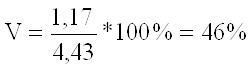 (отже сукупність якісно однорідна);

По заводу:

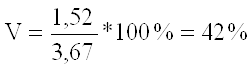 (отже сукупність якісно неоднорідна).

Завдання №6.

Представивши сукупність робітників заводу, як генеральну, сформулювавши вибіркову сукупність, відібравши кожного п'ятого робітника. Для вибіркової сукупності:

а)побудувати графік кореляційного поля для залежності ЗРП від розряду;

б)розрахуйте параметри лінійного рівняння регресії;

в)за допомогою коефіцієнта кореляції оцініть тісноту зв'язку і визначте його достовірність.

Розв'язання:

а) Для початку зазначу, що генеральною сукупністю називають всю кількість значень, які підлягають вибірковому спостереженню. Вибіркове спостереження — це спостереження, при якому із генеральної сукупності (N) випадково відбирають п одиниць, які складають вибіркову сукупність. Для відібраних одиниць обчислюють узагальнюючі характеристики, а потім результати вибіркового спостереження розповсюджуються на всю генеральну сукупність (репрезентативність вибіркової сукупності).

Тож сформулюємо вибіркову сукупність робітників заводу (результати помістимо в таблицю):

Розряд	Заробітна плата
2	104,13
4	137,15
3	123,5
3	123,5
1	91,46
3	133
3	133
6	196
5	163,8
6	196
5	163,8
	=1565,34

б) Рівняння регресії записується:

 

де параметр а₀ показує осереднений вплив на результативну ознаку не врахованих факторів; а параметр а₁ — на скільки змінюється, в середньому, значення результативної ознаки при збільшенні факторної на одиницю.

В свою чергу:

Розрахунки для зручності зведемо в таблицю:

№п/п	Розряд (X)	Заробітна плата (Y)	Y*Х	X2	Yx
1	2	104,13	208,26	4	106,6639
2	4	137,15	548,6	16	148,1059
3	з	123,5	370,5	9	127,3849
4	3	123,5	370,5	9	127,3849
5	1	91,46	91,46	1	85,94295
6	3	133	399	9	127,3849
7	3	133	399	9	127,3849
8	6	196	1176	36	189,5478
9	5	163,8	819	25	168,8268
10	6	196	1176	36	189,5478
11	5	163,8	819	25	168,8268
Разом	41	1565,34	6377,32	179	1567,002
В серед.	3,72	142,304	579,756	16,27	142,4547

Для подальшого розв'язку нам потрібні ще деякі розрахунки:

(Yх-Y)2	(Y-Y)2	(Y-Yx)2	(Х-Х)2
1270,215302	1457,25428	6,420751	2,9584
33,66157946	26,563716	120,0309	0,0784
222,5798432	353,590416	15,09237	0,5184
222,5798432	353,590416	15,09237	0,5184
3176,567957	2585,11234	30,43784	7,3984
222,5798432	86,564416	31,52946	0,5184
222,5798432	86,564416	31,52946	0,5184
2231,976638	2883,26042	41,63088	5,1984
703,4605112	462,078016	25,26902	1,6384
2231,976638	2883,26042	41,63088	5,1984
703,4605112	462,078016	25,26902	1,6384
= 11241,63851	= 11639,9169	= 383,9329	= 26,1824

Отже лінійне рівняння регресії запишеться: якщо а₁ = 20,72097 та а₂ = 65,22198, тоді Y_x = 65,198 + 20,72097*X. Судячи по рівнянню регресії можна сказати, що зв'язок між розрядом і розміром ЗРП - прямий; при зростанні розряду на одиницю ЗРП зростає, в середньому, на 20,72097; а 65,198 - це показник впливу неврахованих факторів.

На основі отриманих даних побудуємо графік кореляційного поля для залежності ЗРП від розряду:

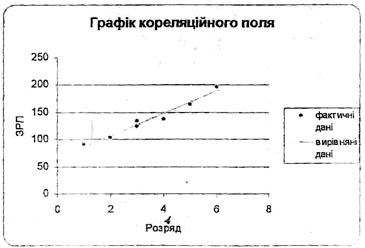
в) Як відомо, кореляція - це залежність коли кожному значенню X відповідає множина значень Y. Одним із завдань теорії кореляції є визначення тісноти зв'язку. Для всіх форм зв'язку (криволінійного, прямолінійного) тіснота оцінюється за допомогою кореляційного співвідношення:

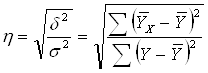
 — дисперсія в ряду вирівняних значень Y;

 — дисперсія в ряду фактичних значень Y.

де D - коефіцієнт детермінації.

Коефіцієнт детермінації - характеризує ту частину варіації результативної ознаки Y, яка відповідає лінійному рівнянню регресії; він показує яку питому вагу у загальній дисперсії ознаки Y займає дисперсія, викликана варіацією фактора X.

Тож знайдемо ці два показники:

, відповідно: D = 0,966 ² = 0,933

Це означає, що зв'язок тісний і ЗРП на 93,3% залежить від розряду.

У випадку лінійної залежності тісноту зв'язку вимірюють лінійним коефіцієнтом кореляції, який знаходиться в межах [-1;1]:

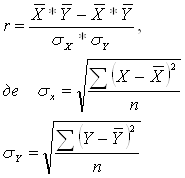
Для даного випадку:

,

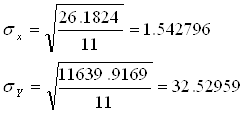тоді 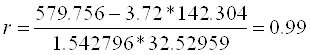 це характеризує прямий тісний зв'язок.

Показник R характеризує індекс кореляції або теоретичне кореляційне співвідношення; знаходиться в таких межах [0;1]:

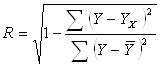Для даних значень:

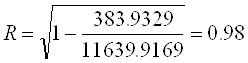 зв’язок - тісний.

За залежністю: r = R = η = отримаємо: 0,99=0,98=0,96=0,96.

Завдання №7.

Відомі дані про оплату праці в цеху:

Таблиця 6

№п/п	Професії робітників	Заг. сума коштів на оплату праці за період, тис.грн.(F)		Середньоспискова чисельність за період, чoл.(t)		Середня ЗРП (f)
		базисний період	звітний період	базисний період	Звітний період	базисний період	звітний період
1	слюсарі	3200	5460	30	42	106,667	130
2	токарі	2900	3120	20	20	145	156
3	штампувальники	3640	2750	15	10	242,667	275
Разом	X	9740	11330	65	72	494,334	561

Обчисліть:

а)Індекси середньої ЗРП по кожній групі робітників;

б)Індекси середньої заробітної плати, фіксованого складу та структурних зрушень;

в)Загальні індекси фонду оплати праці і чисельності робітників (охарактеризуйте їхній взаємозв'язок з індексом середньої ЗРП).

г)Сформулюйте висновки.

Розв’язання:

Індекси - показники, які дозволяють аналізувати зміну явища у часі і просторі, а також оцінювати ступінь виконання плану. Це особлива відносна величина, за допомогою якої можна вивчати безпосередньо неспівставні явища.

За ступенем охоплення елементів сукупності розрізняють:

о Індивідуальні - результат порівняння двох показників у звітному і базисному періодах; визначається у відсотках або в одиницях або в долях від одиниці. Наприклад: ціна одиниці товару звітного періоду поділити на ціну одиниці товару базисного періоду:

і_р=Р₁/Р₀;

Групові - порівнюють певні групи;

Загальні - виражають співвідношення між складними соціально-економічними явищами з неспівставними елементами або з окремих частин всіх явищ; складаються з двох частин: індексуючої величини та вимірника (ваги).

Як відомо на зміну середнього значення показника впливає як зміна середнього значення ознаки, так і зміна ваги.

Якщо в чисельнику і знаменнику вага фіксується на рівні одного періоду, то такий індекс називається індексом фіксованого складу.

,

де p₁ iq₁ - відповідно ціна і обсяг звітного періоду,

а р_о і q_o - ціна і обсяг базисного періоду.

Індекс змінного складу - це співвідношення середніх значень показника у звітному і базисному періодах:

Для відображення впливу змін в структурі сукупності, що вивчається, на динаміку явища визначається індекс структурних зрушень:

а) і_с = 130/106,667 = 1,219

ЗРП слюсарів в середньому збільшилась на 21,9%.

і_т = 156/145 = 1,076

ЗРП токарів в середньому збільшилась на 7,6%.

і_ш = 275/242,667 = 1,133

ЗРП штампувальників в середньому збільшилась на 13,3%.

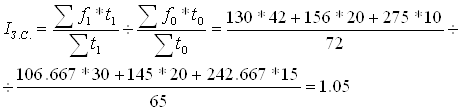
Загальна ЗРП в середньому збільшилась на 5%.

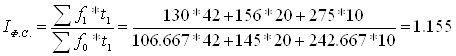
В розрахунку на одного робітника по кожній професії середня ЗРП збільшилась на 15,5%.

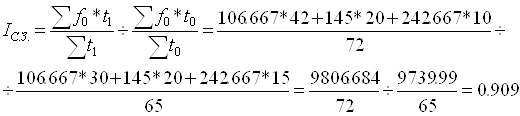
В результаті структурних зрушень середня ЗРП на одного робітника зменшилась на 9,1%.

Між цими показниками існує залежність:

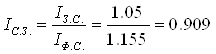
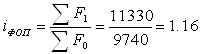
Індекс показує, що фонд оплати праці збільшився на 16%

Судячи по результату можна сказати, що середньоспискова, чисельність зросла на 10,8%.

Відоме співвідношення:

Висновки

Отже, провівши розрахунки, я прийшла до таких висновків:

ü  Найбільша чисельність робітників першого цеху мають І-П розряд зі стажем роботи 1-2 та 3-4 роки (5 чол. або 45,46% від загальної чисельності). Найбільш розповсюдженою є місячна ЗРП в розмірі 91,46-117,66 і 117,66-143,86 грн.(по 44%). Найбільша доля робітників мають III розряд (28%). Переважна більшість отримує заробітну плату у розмірі 117,66 грн. Половина отримує ЗРП меншу за 121,33 грн., а половина — більшу.

ü  Найбільша чисельність робітників другого цеху мають III-IV розряд зі стажем роботи 9 і більше років (11 чол. або 78,57% від загальної чисельності). Найбільш розповсюдженою є місячна ЗРП в розмірі 143,86-170,06 грн.(56,67%). Найбільша доля робітників мають IV розряд (33,34%). Переважна більшість отримує заробітну плату у розмірі 158,79 грн. Половина отримує ЗРП меншу за 157,75 грн., а половина - більшу.

ü  Найбільша чисельність робітників заводу мають III-IV розряд зі стажем роботи 9 і більше років (14 чол. або 56% від загальної чисельності). Найбільш розповсюдженою є місячна ЗРП в розмірі 143,86— 170,06грн.(34,55%). Найбільша доля робітників мають IV розряд (25,45%). Переважна більшість отримує заробітну плату у розмірі 150,93 грн. Половина отримує ЗРП меншу за 142,98 грн., а половина - більшу.

ü  Дослідивши зв'язок між ЗРП і розрядом бачимо, що між ними існує суттєвий тісний зв'язок.

ü  Дослідивши зміни ЗРП, ФОП, ч бачимо:

·  ЗРП слюсарів зросла на 21,9% у звітному періоді порівняно з базисним;

-   ЗРП токарів зросла на 7,6% у звітному періоді порівняно збазисним;

·  ЗРП штампувальників зросла на 13,3% у звітному періоді

·  порівняно з базисним;

·  Під впливом зростання індивідуальних ЗРП і структурних зрушень

·  ЗРП зросла на 5%;

·  За рахунок зростання індивідуальних ЗРП, ЗРП зросла на 15,5%; Внаслідок зміни структури виробництва ЗРП зменшилась на 9,1%;

·  В загальному ФОП збільшився на 16% у порівнянна з базисним роком; а середньоспискова чисельність збільшилась на 10,8%.

Список використаної літератури

 

1.  Гетало А.В., Борух В.О Економічна статистика: Навч. Посібник. К.: ТОВ «УВПУ»ЕК Об», 2002, - 214 с.

2.  Головач А.В., Єріна А.М., Кзирев О.В. та ін Статистика. Збірник задач: навчальний посібник. – К.: Вища школа, 1994.-448 с.

3.  Економічна статистика: Навч. Посібник. / за ред.. Р.М. Моторіна. К.: КНЕУ 2005.

4.  Єріна А.М., Мазуренко О.К., Кальян З.О. Економічна статистика: Практикум. - К.: ТОВ «УВПУЕкс Об», 2002, - 232 с.

5.  Завінська Г.П., Економіка праці: Навч. Посібник. К.: КНЕУ, 2003.-300 с.

6.  Захожний В. Статистика праці і зайнятості. К.: МАУП, 200. – 80 с.

7.  Кулинюг О.І. Економічна статистика: Навчальний посібник. – Хмельницький: Поділля, 200. – 286 с.

8.  Особливості статистичного аналізу діяльності основних галузей матеріального виробництва і обігу суспільного продукту: Навч. Посібник / За заг. ред. О.В. Козирєва. – К.: НМК 80, 1991.

9.  Статистика: Підручник / С.С. Герасименко А.В. Головач, А.М. Єріна та ін. / за наук. Ред.. С.С. Герасименко – 2-ге вид., перероб. І доп. – К.: КНЕУ, 200 – 460 с.

10.  www.ukrstat.gov.ua – офіційний сайт Державного комітету статистики України.