Навигация
Прогнозирование уровня кредиторской задолженности
3.4 Прогнозирование уровня кредиторской задолженности
Под прогнозом понимается научно обоснованное суждение о возможных состояниях объекта в будущем, об альтернативных путях и сроках его осуществления.
Задача экономического прогнозирования, с одной стороны, выяснить перспективы ближайшего или более отдаленного будущего в исследуемой области, руководствуясь реальными процессами действительности, а с другой – способствовать выработке оптимальных текущих и перспективных планов, опираясь на составленный прогноз и оценку принятого решения с позиций его последствий в прогнозируемом периоде. В настоящее время, по оценкам ученых, насчитывается свыше 150 различных методов прогнозирования. Однако на практике используется в качестве основных 15-20. Методы прогнозирования можно разделить на две группы: эвристические (интуитивные) и экономико-математические методы, в которых превалируют объективные начала. При использовании экономико-математических методов структура моделей устанавливается и проверяется экспериментально в условиях, допускающих объективное наблюдение и измерение. К их числу относят статистические методы, методы прогнозной экстраполяции, корреляционный анализ, регрессионный анализ, метод наименьших квадратов и т.д. В зависимости от целей анализа различают: детерминированные модели и стохастические модели. В основе детерминирования лежит положение о существовании причинности, т.е. такой связи явлений, при которой одна причина при определенных условиях порождает другую (следствие). Стохастический анализ предполагает изучение массовых эмпирических данных путем построения моделей изменения показателей за счет факторов, не находящихся в прямых связях, в прямой взаимозависимости и взаимообусловленности. Эти методы изучения связей, как и любые, разрабатываемые в рамках математических наук, сопровождаются целым рядом оговорок и допущений. Несмотря на существенную условность применения в экономическом анализе стохастических моделей, они достаточно распространены. Для корректного использования методов математической статистики (например корреляционно-регрессионного анализа) желательна проверка нормальности законов распределения переменных.
При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта. Экстраполяционные методы являются одним из самых распространенных и наиболее разработанных среди всей совокупности методов прогнозирования. В рыночных условиях ключевым фактором деятельности предприятия является реализация продукции, которая определяет объем производства. Исходя из этого, осуществляется разработка планов использования материалов, уровня запасов, дебиторской, кредиторской задолженности, использования денежных средств. Целью данного исследования является определение оптимального размера краткосрочного заемного капитала в зависимости от планируемого объема производства, исходя из плана реализации продукции.
На основе данных за последние 9 кварталов деятельности предприятия ОАО СЗКО «Молот» построим график изменения выручки от реализации продукции .
| Период | 2000 г. | 2001 год | 2002 год | ||||||
| IV кв. | I кв. | II кв. | III кв. | IV кв. | I кв. | I кв. | II кв. | V кв. | |
| Объем реализации, тыс.грн. | 1392,4 | 62,2 | 365,3 | 689,7 | 885,1 | 645 | 126,1 | 459,4 | 212,5 |
Таблица 3.7 Объем реализации продукции ОАО СЗКО «Молот» в 2000-2002 гг.
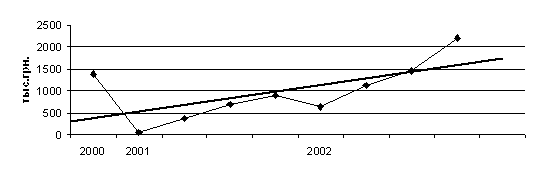
Рисунок 3.3 Изменение уровня выручки от реализации продукции за 2000-2002гг.
Построим линию тренда для кривой развития рассматриваемого показателя. Под трендом понимается характеристика основной закономерности движения во времени, в некоторой мере свободной от случайных воздействий. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории. При помощи метода экстраполяции определим планируемый объем реализации на 2003 год, и на основе полученных данных можно определить остальные плановые показатели хозяйственной деятельности предприятия.
Стохастическое моделирование можно применять в анализе хозяйственной деятельности, если есть возможность составить совокупность наблюдений. У нас есть статистические данные (ряд экспериментальных точек xi;yi) об объемах реализации продукции и об уровне кредиторской задолженности за ряд периодов. В условиях инфляции всякая отсрочка платежа дебиторов приводит к тому, что организация реально получает лишь часть стоимости выполненных работ. Предприятию можно рекомендовать расширить систему авансовых платежей. Нас интересует каков должен быть уровень кредиторской задолженности по полученным авансам при изменении объема реализации продукции. Для того, чтобы вывести формулу зависимости между рассматриваемыми переменными воспользуемся методом линейно-регрессионного анализа. Регрессионный анализ – это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется результативный (зависимый) показатель Y при изменении любого из независимых показателей (факторов) Xi, и имеет вид:
y = ¦ (x1, x2, …, xn) (3.1)
где xi- независимая переменная, фактор;
yi – зависимая переменная, следствие ;
n - число наблюдений .
Анализируя представленные в таблице 3.7 данные, естественно предположить, что при увеличении объема реализации продукции уровень кредиторской задолженности будет расти, т.е. зависимость между объемом реализации и уровнем кредиторской задолженности носит линейный характер. Формула зависимости результата (уровня кредиторской задолженности) от изменений объема реализации будет иметь вид однофакторного линейного уравнения регрессии: y = a + bx
Количество наблюдений при прямолинейной зависимости должно быть не менее 6 (это будут кварталы). На этапе графического анализа нанесем точки на плоскость и по характеру расположения точек на рисунке 3.3 можно сделать вывод о том, что наше предположение о характере зависимости верно. Соединив последовательно точки на плоскости, получим эмпирическую линию регрессии и по ней сделаем предположение о теоретической линии регрессии. Если наблюдается тенденция равномерного возрастания (или убывания) значений признака, то зависимость называется линейной. Процесс нахождения теоретической линии регрессии заключается в выборе и обосновании типа кривой и расчета параметров уравнения регрессии. Способ расчета параметров уравнения регрессии основан на требовании максимальной близости ее к эмпирической линии регрессии. В качестве критерия в математике предложен способ «метод наименьших квадратов», суть которого состоит в минимизации суммы квадратов отклонений фактических значений результативного признака от его расчетных значений.
Таблица 3.8 Показатели хозяйственной деятельности ОАО СЗКО «Молот» за 2000-2002гг.
Тыс.грн.
| Период | 2001 год | 2002 год | ||||||
| I кв. | II кв. | III кв. | IV кв. | I кв. | I кв. | II кв. | IV кв. | |
| Объем реализации | 62,2 | 365,3 | 689,7 | 885,1 | 645 | 1126,1 | 1459,4 | 2212,5 |
| Кредиторская задолженность | - | 365,8 | 221,9 | 458,2 | 363,4 | 595,1 | 626,7 | 1077,0 |
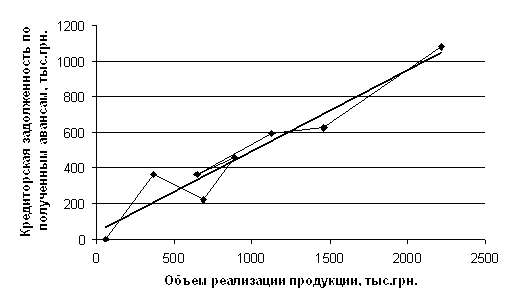
Рисунок 3.3 График зависимости уровня кредиторской задолженности от объема реализации продукции ОАО СЗКО «Молот».
Для линейной регрессии y= ax + b значения параметров a и b находятся по следующим формулам:
b = (åxiåyi - nåxiyi ) / ((åxi)2 - n åxi2 ) ( 3.2)
a = (åyi - båxi ) / n (3.3)
где xi- независимая переменная, фактор (объем реализованной продукции);
yi – зависимая переменная, следствие (уровень кредиторской задолженности);
n - число наблюдений .
Рассчитаем параметры уравнения для анализируемого периода:
b = 40,6634543 ; a = 0,4543527
Уравнение имеет вид: y = 0,4543527 х + 40,6634543, коэффициент регрессии при х показывает, что при увеличении объема реализации на тысячу гривен уровень кредиторской задолженности увеличится на 454 гривны. В ходе регрессионного анализа решаются две основные задачи: построение уравнения регрессии, т.е. нахождения вида зависимости между результативным показателем и независимыми факторами; оценка значимости полученного уравнения, т.е. определение того насколько выбранные факторные признаки объясняют вариацию признака Y. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев. Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (`e ), называемого средней ошибкой аппроксимации:
`e = 1/n å(( yхk – `y) / yk )2 * 100% (3.4)
где yk - k-е фактическое значение результативного показателя;
yхk- рассчитанное по уравнению регрессии значение результативного показателя.
`y - среднее значение, рассчитанное по уравнению
`y = 1/n åyхk; `y =251,35 тыс.грн.
| Х, тыс грн. | yхk, тыс.грн. | yхk– `y | yk, тыс.грн. | (yхk – `y)/yk | (( yхk – `y)/yk )2 |
| 62,2 | 40,6635 | -210,69 | х | х | х |
| 365,3 | 206,935 | -44,415 | 365,8 | -0,121417673 | 0,014742251 |
| 689,7 | 141,527 | -109,82 | 221,9 | -0,494922928 | 0,244948705 |
| 885,1 | 248,935 | -2,4148 | 458,2 | -0,005270106 | 2,7774E-05 |
| 645 | 205,845 | -45,505 | 363,4 | -0,125221488 | 0,015680421 |
| 1126,1 | 311,162 | 59,8122 | 595,1 | 0,100507891 | 0,010101836 |
| 1459,4 | 325,526 | 74,1758 | 626,7 | 0,118359378 | 0,014008942 |
| 2212,5 | 530,207 | 278,857 | 1077 | 0,258919937 | 0,067039534 |
| итого | 2010,8 | х | х | х | 0,366549464 |
| `e | х | х | х | х | 4,5818683 |
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпирической), те меньше средняя ошибка аппроксимации. Модель считается пригодной для практического использования, если средняя ошибка аппроксимации не превосходит 5%-8 %. В анализируемой ситуации ошибка аппроксимации составит 4,6 %. Можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемую зависимость. Для оценки качества уравнения регрессии используются еще несколько критериев: коэффициент детерминации, критерий Фишера (показывает соответствие совокупности генеральных данных общей совокупности), критерий Стьюдента (оценка значимости каждого параметра уравнения), коэффициент эластичности (показывает на сколько процентов изменяется в среднем результативный показатель при изменении фактора на один процент) и т.д. Коэффициент детерминации R2 (квадрат коэффициента корреляции) характеризует долю вариации зависимой переменной Y, которая объясняется действием включенных в модель факторных признаков.
R2 = 1 – (å(yk – yхk)2 / å( yk–`yk)2) (3.5),
где `yk = 1/n åyk(3.6)
Произведя расчеты, получим среднюю арифметическую`yk= 463,51, а коэффициент детерминации R2 = 0,92. Это означает, что 92 % вариации зависимой переменной объясняется включенными в модель факторами, а 8 % - другими причинами, т.е. факторами не представленными в модели. Если коэффициент R2 близок к единице, то связь между исследуемыми явлениями очень тесная и наоборот.
Таким образом в результате анализа была построена регрессионная зависимость (т.е. проведен регрессионный анализ) и рассчитаны коэффициенты ее тесноты и значимости (т.е. проведен корреляционный анализ). Выведенная зависимость имеет вид уравнения
y = 0,4543527 х + 40,6634543,
при помощи которого можно прогнозировать динамику уровня кредиторской задолженности предприятия по полученным авансам при планировании изменения объемов реализации продукции на ОАО СЗКО «Молот».
0 комментариев