Определение усилий

5.1 Определение усилий

Усилия в зацеплениях представляются в виде трёх составляющих: окружной P, радиальной T и осевой (аксиальной) Q. Окружное усилие P направлено по касательной к делительной окружности по направлению движения для ведомого колеса и против движения для ведущего колеса; радиальное усилие T направлено к центру колеса, осевое Q - вдоль оси.

Усилия в зубчатых передачах вычисляются по формулам:

Цилиндрическая прямозубая передача.

Окружное усилие.

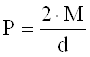(19)

Радиальное усилие.

(20)

где α - угол зацепления, для эвольвентных зубчатых колёс α = 20⁰.

Используя формулы (22) и (23), получаем следующие значения.

Окружное и радиальное усилия, действующие на шестерню 5.

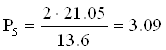 Н

 Н

Окружное и радиальное усилия, действующие на колесо 4.

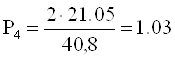 Н

 Н

Окружное и радиальное усилия, действующие на колесо 6.

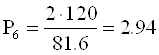 Н

 Н

5.2 Компоновочная схема

Компоновочная схема редуктора, с усилиями в зацеплениях колёс, представлена на рис. 4.

Она представляет собой эскизный упрощённый вариант конструкции.

 

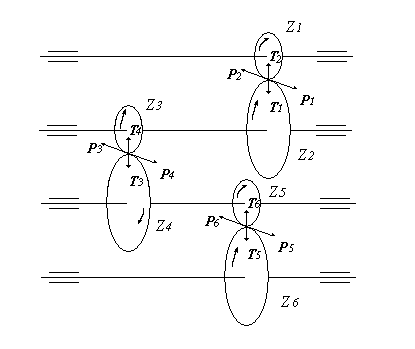
Рисунок 4 - Компоновочная схема редуктора

5.3 Расчет длины вала

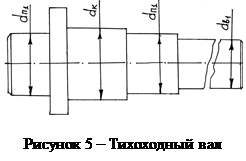
Зная размеры зубчатых колес, составляется эскизная компоновка механизма (рис. 5) и определяются необходимые размеры валов. Расстояние l₁ между серединами левого и правого подшипника определяется по формуле

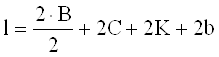
где B_n- ширина подшипника , мм.

С – зазор между стенкой корпуса и колеса, мм.

K – ширина ступицы, мм.

b – ширина зуба , мм.

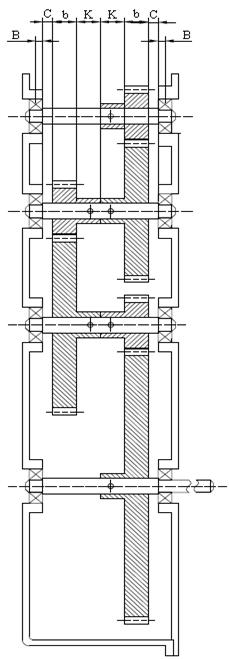
Рисунок 5 - Эскизная компоновка механизма

5.4 Расчёт диаметра предпоследнего вала 5.4.1 Расчётные схемы. Построение эпюр

Расчётная схема предпоследнего вала представлена на рис. 6.

Рисунок 6 - Усилия в зацеплениях колёс предпоследнего вала

Рассмотрим плоский изгиб в плоскости YOZ (рис. 7).

Где  - длина вала, a₁= 7 мм , a₂= 7.5 мм , a₃=22.5 мм ,

Рисунок 7 - Усилия, действующие в плоскости YOZ

Для этого определим реакции в опорах из условий равновесия:

R_B= 0.9 Н

R_А = -0.08 Н

Проверка:

-0,08 + 0.9 – 1.11 + 0.37 = 0

Изгибающие моменты на участках z_i даны в таблице 1.

Таблица 1 - Изгибающие моменты в плоскости YOZ.

0 ≤ x1 ≤ a1	a1 ≤ x2 ≤ a1+a2	0 ≤ x3 ≤ a3
M1 = RA. x1 x1 = 0 , M1 = 0 x1 = a1 , M1 = -0.08 . 7 = -0.56 Н.мм	M2 = RA. x2 + T4. (x2 - a1) x2 = a1 , M2 = -0.56 Н.мм x2 = a1+a2 , M2 = -2.36+8.325 = 5.96 Н.мм	M3 = RB. x3 x3 = 0 , M3 = 0 x3 = a3 , M3 = 0.9 . 7.5 = 6 Н.мм

Эпюра М_Х представлена на рис.

Рисунок 8 - Эпюра М_Х

Рассмотрим плоский изгиб в плоскости XOZ (рис. 9).

Рисунок 9 - Усилия, действующие в плоскости XOZ

Определим реакции в опорах из условий равновесия:

R_B= 1.07 Н

R_А = 0.59 Н

Проверка

0.59+1.07-0.37-1.11 = 0

Изгибающие моменты на участках z_i даны в таблице 2.

Таблица 2 - Изгибающие моменты в плоскости XOZ.

0 ≤ x1 ≤ a1	a1 ≤ x2 ≤ a1+a2	0 ≤ x3 ≤ a3
M1 = RA. x1 x1 = 0 , M1 = 0 x1 = a1 , M1 = 0.59 . 7= 4.13 Н.мм	M2 = RA. x2 - P4. (x2 - a1) x2 = a1 , M2 = 4.13 Н.мм x2 = a1+a2 , M2 = 0.59 . 29.5-0.37 . 22.5 = 9 Н.мм	M3 = RB. x3 x3 = 0 , M3 = 0 x3 = a3 , M3 = 1.07 . 7.5 = 9 Н.мм

Эпюра М_Y представлена на рис. 10.

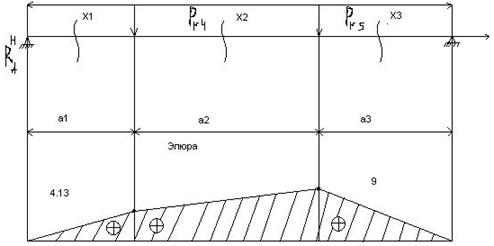
Рисунок 10 - Эпюра М_Y

5.4.2 Расчёт диаметра вала

Диаметр вала определяется из рассмотрения условий прочности.

Наибольшие изгибающие моменты М_хмах = 6 Н^.мм , М_умах = 9 Н^.мм.

Условие прочности для вала представляется в виде:

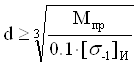(22)

где М_пр - приведённый момент, определяемый по формуле:

(23)

М_Х, М_Y, - изгибающие моменты в опасном сечении в двух перпендикулярных плоскостях;

[σ_-1]_и - предел выносливости при симметричном цикле (для Ст45 [σ_-1]_и = 8000 Н/см²).

Таким образом:

 Н^. см

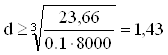 мм

Округляем полученное значение до ближайшего большего значения по ГОСТ 6366-90.

d = 1.6 мм.

5.5 Расчёт диаметра выходного вала 5.5.1 Расчётные схемы. Построение эпюр

Расчётная схема выходного вала представлена на рис. 11.

Рисунок 11 - Усилия в зацеплении колеса выходного вала

Рассмотрим плоский изгиб в плоскости YOZ (рис. 12).

Где  - длина вала, ,  .

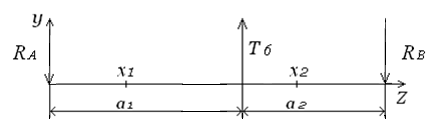
Рисунок 12 - Усилие, действующее в плоскости YOZ

Определим реакции в опорах из условий равновесия:

 Н

 Н

Проверка

-0.8+1.05-0.24=0

Изгибающие моменты на участках z_i даны в таблице 3.

Таблица 3 - Изгибающие моменты в плоскости YOZ

0 ≤ X1 ≤ a1	0 ≤ X2 ≤ a2
M1 = RA. x1 x1 = 0 , M1 = 0 x1 = a1 , M1 = 25.5 . (-0.24) = -6 Н.мм	M2 = RB. x2 x2 = 0 , M3 = 0 x2 = a2 , M2 = 7.5 . (0.8)= -6 Н.мм

Эпюра М_Х показана на рис. 13.

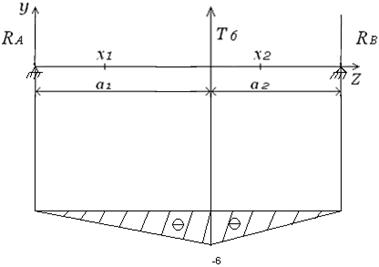
Рисунок 13 - Эпюра М_Х

Рассмотрим плоский изгиб в плоскости XOZ (рис. 14)

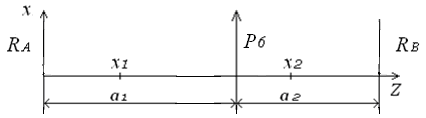
Рисунок 14 Усилие, действующее в плоскости XOZ.

Определим реакции в опорах из условий равновесия:

 Н

 Н

Проверка

-1.05+0.72+0.3=0

Изгибающие моменты на участках z_i даны в таблице 4.

Таблица 4 - Изгибающие моменты в плоскости XOZ

0 ≤ X1 ≤ a1	0 ≤ X2 ≤ a2
M1 = RA. x1 x1 = 0 , M1 = 0 x1 = a1 , M1 = 0.3 . 5.5 = 6 Н.мм	M2 = RB. x2 x2 = 0 , M3 = 0 x2 = a2 , M2 = 7.5 . 0.72 = 6 Н.мм

Эпюра М_Y показана на рис. 15.

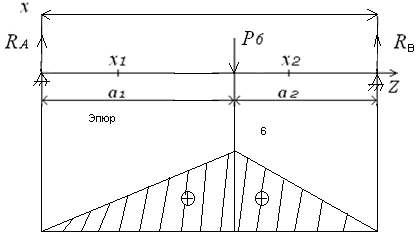
Рисунок 15 - Эпюра М_Y

5.5.2 Расчёт диаметра выходного вала

Наибольшие изгибающие моменты М_хмах = 6 Н^.мм , М_умах = 0 Н^.мм.

Таким образом, используя формулы (22) и (23), получаем

 Н^. см

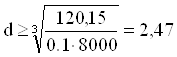 мм

Округляем полученное значение до ближайшего большего значения по ГОСТ 6366-90.

d = 3 мм.

6 Расчёт и выбор подшипника 6.1 Выбор подшипника

Выбор типа подшипника зависит от отношения осевой силы F_Aрадиальной F_r. В разрабатываемом редукторе присутствуют только прямозубые зубчатые колеса следовательно выбираются радиальные шарикоподшипники , так как

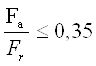
На основе полученного значения диаметра выходного вала (d = 3 мм), выбираем подшипник радиальный 1 000 092, параметры которого приведены в таблице 5 и таблице 6.

Таблица 5 - Параметры шарикоподшипника радиального однорядного 1 000 094 ГОСТ 8338-57

Размеры, мм			Шарики
d	D	B	Dw, мм	Z
3	8	3	1.59	6

Таблица 6 - Ориентировочные расчётные параметры

Грузоподьёмность, Н
Динамическая (С)	Статическая (С0)
440	200

Размеры подшипника обозначены на рис. 16.

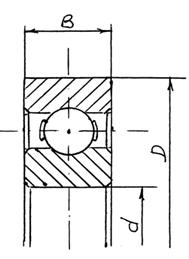
Рисунок 16 - Размеры подшипника 1 000 092

6.2 Расчёт подшипника на долговечность

Теоретическая расчётная долговечность L в млн. оборотов определяется по формуле

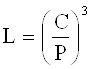(24)

где С - динамическая грузоподъёмность подшипника;

Р - эквивалентная динамическая нагрузка определяется по эмпирическим формулам и зависит от действующих на подшипник сил, характера нагрузки и температуры.

Долговечность подшипника в часах

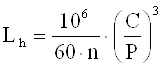(25)

где n - частота вращения кольца подшипника в минуту (n_вых'). Для приборных зубчатых редукторов ресурс работы подшипников устанавливаеться в пределах 1000-10000 ч.

Эквивалентная динамическая нагрузка Р для однорядных радиальных и радиально-упорных шарикоподшипников

(26)

где К_δ - коэффициент, учитывающий влияние динамических условий работы (К_δ = 1);

К_Т - коэффициент, учитывающий влияние температурного режима работы на долговечность подшипника (К_Т = 1);

ν - коэффициент, учитывающий какое кольцо вращается; при вращении внутреннего кольца ν = 1; наружного кольца ν = 1.2 (кроме радиального шарикового сферического, радиально-упорного шарикового магнитного, для которых в любом случае ν = 1);

X и Y - коэффициенты радиальной и осевой нагрузок соответственно, назначаемые в зависимости от параметра осевой нагрузки (при отсутствии осевой нагрузки - X = 1, Y = 0).

F_r - радиальная нагрузка;

F_a - осевая нагрузка

Радиальная нагрузка определяется, как наибольшая величина, полученная из следующих уравнений

(27)

(28)

Где R_A, R_B, R_A, R_B - реакции опор в обоих подшипниках одного вала, разложенные по осям. Эквивалентная статическая нагрузка P₀ для радиальных, радиально-упорных шарикоподшипников выбирается как наибольшая величина, полученная из уравнений.

Используя формулы (27) и (28), получим следующие значения радиальных нагрузок на подшипниках выходного вала

 Н

 Н

Поскольку  , то

F_r = F_r1 = 21.34 Н

Определим эквивалентную динамическую нагрузку по формуле (26)

 Н

Пользуясь данными из таблицы 6 и формулами (24) и (25), получим номинальную долговечность

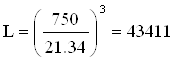 млн.об.

или

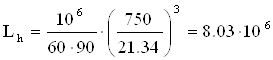 ч.