Навигация
Кінематичні параметри. Окружні швидкості на шківах
1.3.1. Кінематичні параметри. Окружні швидкості на шківах
v1 = d1 n1 / 60 ; v2 = d2 n2 / 60. (1.1)
Враховуючи жорстке ковзання ременя, можна записати v1 < v2 чи
v2 = v1 (1—ε). (1.2)
де ε – коефіцієнт ковзання. При цьому передаточне відношення
i = n1 / n2 = v1 d1 = d2 / [ d1 (1—ε) ]. (1.3)
В подальшому показано, що величина ε залежить від навантаження, тому в ременній передачі передаточне відношення не завжди є постійним. При нормальних робочих нагрузках ε ≈ 0,01…0,02. Найбільше значення ε дозволяє наближено приймати:
 i ≈ d2 / d1. (1.4)
i ≈ d2 / d1. (1.4)
1.3.2 Геометричні параметри
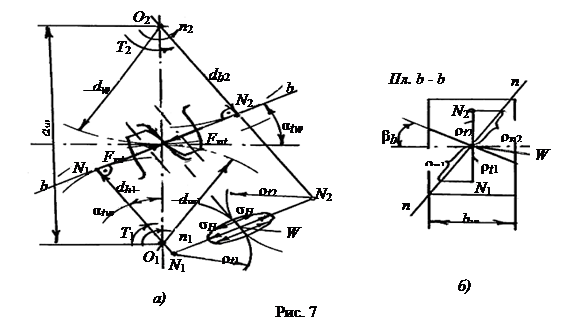
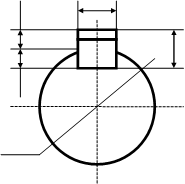
 На рис1.7, а – міжосьова відстань; β – кут між гілками ременя; α – кут обхвату ременем малого шківа. При геометричному розрахунку відомими зазвичай є d1, d2 і а, які визначають кут і довжину ременя l. В результаті витяжки і провисання ременя значення α і l не являються точними і визначаються приблизно так:
На рис1.7, а – міжосьова відстань; β – кут між гілками ременя; α – кут обхвату ременем малого шківа. При геометричному розрахунку відомими зазвичай є d1, d2 і а, які визначають кут і довжину ременя l. В результаті витяжки і провисання ременя значення α і l не являються точними і визначаються приблизно так:
α = 180°— β ; sin (β/2) = (d2— d1) / (2a) (1.5)
Враховуючи, що β/2 практично не перевищує 15°, приблизно приймаємо значення синуса рівним аргументу і запишемо
β = (d2 — d1) / а рад ≈ 57 ( — d1) / а° (1.6)
Довжина ременя вираховується як сума прямолінійних ділянок і дуг обхвату:
l ≈ 2a + 0,5 (d2 + d1) / (4а) (1.7)
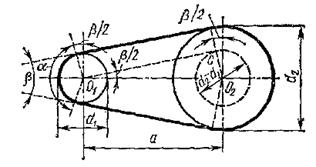
Рис. 1.7 Геометричні параметри передачі
1.3.3 Сили та силові залежності
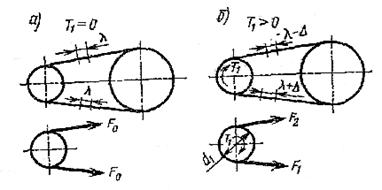 |
На рис.1.8 показане навантаження гілок ременя у двох випадках: Т1 = 0 (рис.1.8,а) і Т1 > 0 (рис.1.8,б). Тут позначено Fo – початковий натяг ременя ; F1 і F2 –натяг ведучої та веденої гілок в навантаженій передачі; Ft = 2 T1 / d1 – окружна сила передачі.
Рис. 1.8 Сили та силові залежності
За умовою рівноваги шківа маємо:
T1 = 0,5 d1 (F1 – F2) (1.8)
або
F1 – F2 = Ft (1.9)
Зв’язок між Fo, F1 та F2 можна встановити на основі наступних роздумів.
Геометрична довжина ременя не залежить від навантаження [див. формулу (1.7)] і залишається незмінною як в ненавантаженій, так і в навантаженій передачі. З цього випливає, що додаткова витяжка ведучої гілки компенсується рівним скороченням веденої гілки (рис.1.8). Запишемо:
F1 = Fo + ∆F , F2 = Fo – ∆F (1.10)
або
F1 + F2 = 2Fo (1.11)
Із рівнянь (1.10) і (1.11) випливає:
F1 = Fo + Ft / 2 , F2 = Fo – Ft / 2 (1.12)
Отримали систему двох рівнянь з трьома невідомими Fo, F1 та F2. Ці рівняння встановлюють змінення натягу ведучої чи веденої гілок в залежності від навантаження Ft, але не дозволяють передавати це навантаження чи тягову передачу, яка зв’зана з величиною сили тертя між ременем і шківом. Така залежність встановлена Ейлером.
2 ПРУЖИНИ
2.1 Призначення та конструкції пружин
Пружні елементи, або пружини, належать до розповсюджених деталей, що використовуються в різних машинах, механізмах та приладах. Вони виконують інколи дуже відповідальні та складні функції.
Пружні властивості пружин дають змогу використовувати їх у таких випадках:
а) для створення потрібних постійних зусиль (у натискних та натяжних пристроях передач тертям, муфтах, гальмах, клапанах);
б) для акумулювання механічної енергії попереднім деформуванням пружин (пружинні двигуни приладів часу та інші пристрої);
в) для віброізоляції та амортизації ударів за рахунок пружних характеристик відповідним чином підібраних пружин (у транспортних засобах, опорних пристроях чутливих елементів приладів та ін.);
г) для вимірювання сил, що здійснюється фіксацією пружних деформацій пружин (динамометри та інші вимірювальні прилади).
Усі пружини за видом навантаження поділяють на пружини розтягу, стиску, кручення (рис.2.1).
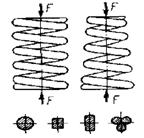 | 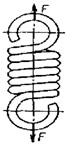 | 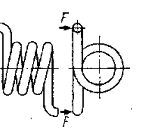 | |||
Рис. 2.1 Види пружніх елементів
У приладобудуванні найрозповсюдженішими є гвинтові пружини розтягу, стиску та кручення, виконані із дроту круглого або іншого перерізу. Гвинтова пружина розтягу виготовляється зі щільним навиванням витків, до того ж крайні витки плавно переходять у спеціальні вушка, які зручні для закріплювання пружини.
Гвинтові пружини стиску бувають циліндричної та конічної форми. Конічна форма забезпечує пружині змінну жорсткість при деформуванні. В таких пружинах стиску робочі витки не дотикаються між собою, а лише крайні витки виконуються зі щільною навивкою для надання пружині плоских опорних торців. Гвинтові пружини стиску найчастіше виготовляють із дроту круглого перерізу, а при великих стискаючих силах застосовують пружини з квадратним або прямокутним перерізом витків. З метою підвищення податливості в умовах обмежених габаритних розмірів використовують багатожильні гвинтові пружини стиску.
2.2 Розрахунок гвинтових циліндричних пружин 2.2.1 Розрахунок гвинтових циліндричних пружин розтягу та стискуГвинтові циліндричні пружини розтягу та стиску мають такі основні геометричні параметри (рис. 2.2 а, б):
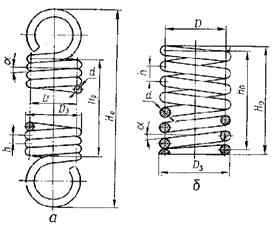
Рис. 2.2 Гвинтові циліндричні пружини розтягу та стиску
d— діаметр витків (дроту) пружини;
D— середній діаметр пружини;
Dз = D + d — зовнішній діаметр пружини;
С = D/d — індекс пружини;
h — крок витків у ненавантаженій пружині (h = d — для пружини розтягу, рис.2.2, a);
α — кут підйому витків (tg α = h/(![]() D);
D);
H0 — довжина (висота) ненавантаженої пружини;
Hp — довжина робочої частини ненавантаженої пружини;
і = Нр/h — кількість робочих витків;
L — довжина дроту для виготовлення пружини.
Податливість циліндричних пружин пропорційна їхньому індексу С. Для збільшення податливості індекс С беруть якомога більшим; практичне застосування мають пружини з індексом С = 4...12. Залежно від діаметра витків рекомендують такі значення індексу C циліндричних пружин:
Таблиця 2.1 Рекомендовані значення індексу С.
| d, мм | <2‚5 | 3—5 | 6—12 |
| С | 5—12 | 4—10 | 4—9 |
Збільшуючи індекс пружини певної жорсткості, можна зменшити довжину пружини через збільшення її діаметра, а зменшуючи індекс, можна зменшити діаметр через збільшення довжини пружини.
Для розрахунку на міцність розглянемо силові фактори, що діють у перерізі витка, навантаженого силою F пружини (рис. 2.3).
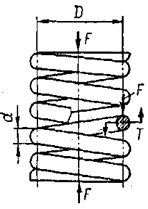
Рис. 2.3 Навантаження витків пружини стиску.
За умовою рівноваги нижньої частини пружини визначаємо, що у довільному перерізі витка діють крутний момент Т = 0‚5FD та поперечна сила F, які спричинюють відповідно кручення та зріз витка. Нехтуючи кутом підйому витків α, який для більшості пружин менший ніж 10—12°, а також напруженнями зрізу від поперечної сили, напруження кручення витків визначають за виразом:
τ = TK/WP = 8FD/(πd3 ), (2.1)
де K — коефіцієнт, що враховує кривину витків; Wp = πd3/16 — полярний момент опору перерізу витка. Коефіцієнт K беруть залежно від індексу С пружини із співвідношення
K=1 + 1‚4/С. (2.2)
Умову міцності витків пружини на основі виразу (2.2) записують у вигляді
τ = 8FDК/(πd3) < [τ]. (2.3)
Потрібний діаметр дроту пружини із умови (2.3) визначають за формулою
![]() . (2.4)
. (2.4)
Якщо в умові (2.3) врахувати, що D/d = С, то формулу для визначення діаметра дроту пружини можна записати у вигляді
![]() (2.5)
(2.5)
Добуте значення d округлюють до значення у стандартному ряду діаметрів дроту для виготовлення пружин.
Діаметр дроту пружини дає змогу визначити середній та зовнішній
діаметри пружини:
D = Сd; D3 = D + d.
Осьову пружну деформацію пружини (розтяг або стиск) під дією навантаження F можна дістати як добуток кута закручування витків θ пружини та середнього радіуса пружини 0‚5D:
λ =0‚5Dθ = 0‚5DТπDі/(GIр) = 0,25FπD3i/(GIp),
де і — кількість робочих витків пружини; G — модуль пружності при зсуві матеріалу пружини (для сталі G = 8 104 МПа); Ip = πd4/32 — полярний момент інерції перерізу витка пружини.
Виражаючи Ip через d та враховуючи, що D/d = С, вираз для осьової пружної деформації пружини можна записати у вигляді
λ = 8FD3i/(Gd4) = 8FС3i/(Gd). (2.6)
Відношення навантаження F до осьової пружної деформації λ пружини називається жорсткістю k пружини. Із виразу (2.6)
k = Gd4/(8D3і) = Gd/(8С3i). (2.7)
Вираз (2.6) дає змогу визначити потрібну кількість робочих витків пружини, якщо відоме значення λ:
і = Gd4λ/(8FD3) = Gdλ/(8FС3). (2.8)
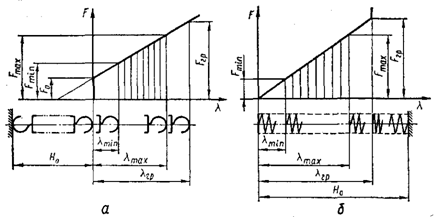 |
Щоб правильно розрахувати та підібрати пружину, треба знати її робочу характеристику (рис.2.4 а, б), на якій повинні бути зазначені: λmіn, λmах — відповідно мінімальна та максимальна розрахункові деформації пружини; Fmin, Fmax, Fгp — відповідно мінімальне і максимальне розрахункові навантаження та граничне навантаження на пружину (при посадці витків у пружинах стиску і за міцністю витків у пружинах розтягу).
Рис. 2.4 Робочі характеристики пружин розтягу та стиску
Для пружин розтягу (рис.2.2, а), виготовлених із щільним (закритим) навиванням витків, початковий натяг (притискання сусідніх витків)
F0 =(0,2...0,3)Fгp. Граничне навантаження для пружин розтягу та стиску беруть Fгp = (1,1... 1,2) Fmax.
Подальший розрахунок пружини розтягу полягає у визначенні з умови міцності діаметра дроту d за максимальним навантаженням Fmах і середнього D та зовнішнього Dз діаметрів пружини. Потім знаходять потрібну кількість робочих витків і за формулою (2.8), беручи максимальне розрахункове навантаження Fmах та деформацію λmах .
Решту розмірів пружин обчислюють за такими формулами:
Похожие работы
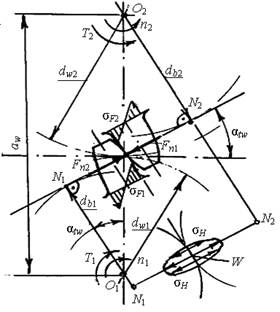
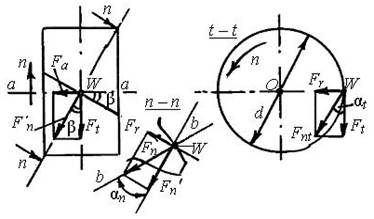
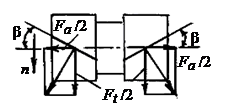
... колес нарезают тем же инструментом, что и прямые, установленным относительно заготовки под углом β. Расчет на прочность принято вести для прямозубой передачи. Для этого все зубчатые и червячные передачи приводятся к эквивалентным прямозубым цилиндрическим. Эквивалентные параметры косозубого цилиндрического колеса (приведение рассматривалось в курсе "Теория машин и механизмов"): делительный ...
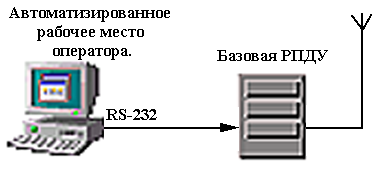
... указания. 1 Цель: 1.1 Изучить наиболее распространенные стандарты систем персонального радиовызова общего пользования. 2 Литература: 2.1 Соловьёв А. А., Смирнов С. И. Техническая энциклопедия пейджинговой связи. Эко-Трендс М:, 1998 стр. 18-50. 2.2 Громов Ю. А. Стандарты и системы подвижной радиосвязи. Эко-Трендс М:, 1998 стр. 39-52 2.3 Приложение к ...
... 195.7 9 2 25.47 392.6 8.49 4 1.3 60.81 164.4 10 2 30.33 329.7 10.11 I - - 76 131.6 I I I 8 1.68 36.09 277.1 12.03 9 1.42 42.96 232.8 14.32 2. Расчет цепной передачи 2.1. Передаточное число передачи u = 3 2.2. Принимаем число зубьев для ведущей звездочки Z1= 25 таб. 11.4 [1] тогда ...
... Направление линии зуба правое. Вращение против часовой стрелки. при bm=35° при bm=35° Направление линии зуба левое. Вращение по часовой стрелке. 7. РАСЧЁТ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ 7.1 Выбор материалов червяка и червячного колеса Для изготовления червяков применяют углеродистые и легированные стали (см. табл. 3.1). Выбор марки стали зависит от назначаемой термообработки ...



0 комментариев