Навигация
1. Для пружин розтягу
довжина робочої частини ненавантаженої пружини (див. рис.2.2.а) Hp = іd повна кількість витків І0 = І + (1...2);
довжина ненавантаженої пружини H0 = і0d + 2hв,
де hв =(0.5...1)D — висота одного вушка; довжина пружини при максимальному розрахунковому навантажені F mах
H=H0 + λmax = H0 + (Fmax - F0)/k = H0 + 8С3 і(Fmax – F0)/(Gd);
довжина дроту для виготовлення пружини
L = πDi/соsα + 2lв,
де lв — довжина дроту для одного вушка.
2. Для пружин стиску
загальна кількість витків і0 = i + (1,5...2), де кількість крайніх щільно навитих витків становить 1,5—2;
мінімальний зазор між витками при максимальному розрахунковому навантаженні Fmax — ∆ = (0,1...0,2) λmax/i, крок витків ненавантаженої пружини h = λmax/i + d + ∆;
довжина пружини, стиснутої до дотику витків, Hгp = (i0 — 0,5) d; довжина ненавантаженої пружини H0 = Hгp + і (h — d); довжина дроту для виготовлення пружини L = πDі0/cos α.
При великій кількості витків довгі пружини стиску під навантаженням можуть втрачати поздовжню стійкість. Тому рекомендують при H0/D > 3 встановлювати пружини стиску на оправках або у відповідних трубках.
2.2.2 Розрахунок гвинтових циліндричних пружин кручення При навантаженні циліндричної пружини кручення зовнішнім моментом М = Fа (рис. 2.5) у поперечних перерізах витків утворюється такий же момент М, вектор якого напрмлений уздовж осі пружини.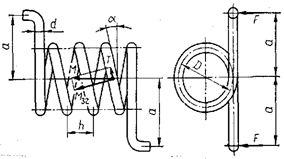 |
Рис. 2.5 Гвинтова циліндрична пружина кручення Якщо розкласти момент М на складові вздовж витка та перпендикулярно до витка, то в поперечному перерізі витка будемо мати крутний Т = М sіn α і згинальний Mзг = М соs α моменти. Оскільки кут підйому витків α < 10°, скручуванням витків можна знехтувати (Т ≈ 0), а розрахунок витків на міцність виконати тільки на згин за згинальним моментом Mзг = М = Fа.
Напруження згину для витків циліндричної пружини кручення визначають за виразом
σ = MaгK'/W0 = З2МК'/(πd3) (2.9)
де K' = (С — 0‚25)/(С — 1) — коефіцієнт кривини витків, що залежить від індексу пружини С = D/d; W0 = πd3/32 — осьовий момент опору перерізу витка (дроту пружини) діаметром d.
На основі виразу (2.9) умову міцності витків на згин записують у вигляді
σ = З2МК'/(πd3) < [σ]. (2.10)
При проектувальному розрахунку пружини кручення діаметр витків (або дроту) визначають за формулою, що випливає із умови (2.10),
![]() (2.11)
(2.11)
Крок витків пружини кручення беруть h = d + (0,2...0,5) мм. Кут закручування пружини під дією моменту М визначають за формулою
φ = МπDі/(ЕІ), (2.12)
де i — кількість робочих витків пружини; Е — модуль пружності матеріалу; I=πd/64 — осьовий момент інерції перерізу витка.
3 КУЛАЧКОВІ МЕХАНІЗМИ
3.1 Загальні положення
Кулачковим називається механізм, що містить дві основних ланки: кулачок і штовхальник, що утворюють вищу кінематичну пару.
Кулачкові механізми знайшли широке застосування в системах газорозподілу ДВЗ, у системах керування електричних ланцюгів, у вагонах метрополітену (контролери).
Достоїнства кулачкових механізмів:
1.можливість відтворення практично будь-якого закону руху вихідної ланки;
2.мала кількість деталей (кулачок і штовхальник), що дозволяє просто виготовляти й обслуговувати.
Недолік:
Наявність вищої кінематичної пари, у якій можуть виникати підвищені питомі тиски, що може привести до руйнування поверхні кулачка.
1 – кулачок
2 – штовхач
3 – ролик
4 – пружина
5 – контакти
Поверхня кулачка, з яким взаємодіє штовхальник - робочий (дійсний) профіль кулачка.
Поверхня, що проходить через точку В віддалена від дійсного профілю на відстані радіуса ролика - теоретичний профіль (рис. 3.1).
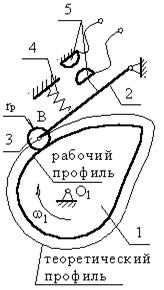
Рис. 3.1 Профіль кулачка
3.2 Основні схеми кулачкових механізмів
Кулачковий механізм із поступально рухаючим штовхальником.
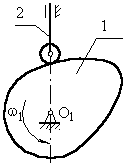 |
 а) з центральним штовхальником (вісь штовхальника проходить через вісь обертання кулачка),(рис.3.2)
а) з центральним штовхальником (вісь штовхальника проходить через вісь обертання кулачка),(рис.3.2) Рис. 3.2 Кулачковий механізм із центральним штовхальником
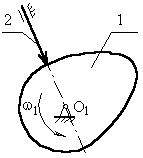
б) з позавісним штовхальником (рис. 3.3). Позавісність ліва, тому що вісь штовхальника проходить праворуч осі обертання кулачка, е – ексцентриситет.
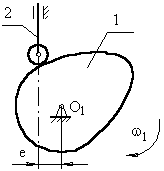
Рис.3.3 Кулачковий механізм із позавісним штовхальником
Кулачковий механізм із поступально рухаючимся товхальником (рис. 3.4), ланка 2 (штовхальник) робить зворотньо-обертовий рух з центром обертання в точці О2.
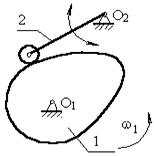
Рис. 3.4 Кулачковий механізм із поступально рухаючимся товхальником
3.3 Основні параметри кулачкових механізмів
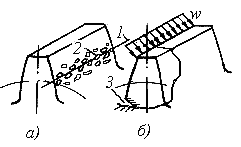
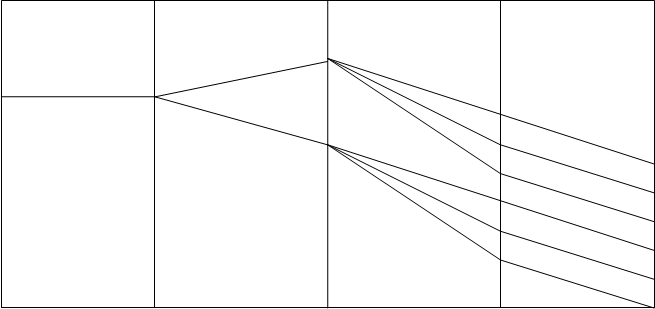
У процесі роботи штовхальник робить 3 рухи (рис. 3.5):
1. поступально вгору - у цьому випадку штовхальник взаємодіє з ділянкою 01;
2. стоїть на місці (вистій) - контакт із ділянкою 12.
Тут постійний радіус кривизни.
3. штовхальник опускається (зближення) - контакт із ділянкою 23.
У першій фазі підйому штовхальника (фаза видалення) на профілі кулачка відповідає кут ψудал;
у фазі вистою – ψвыс;
у фазі зближення – ψсб.ψудал + ψвыс + ψсб = ψраб – робочий кут профілю кулачка
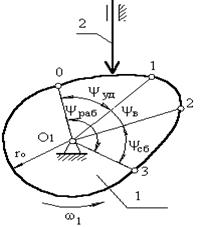
а)
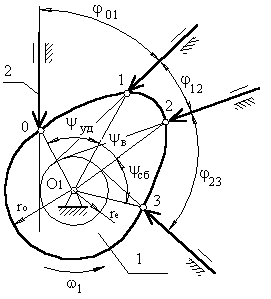
б)
Рис.3.5 Основні параметри кулачкових механізмів
Кут профілю кулачка можна показати тільки на кулачку. Кут повороту кулачка, що відповідає вище зазначеним фазам переміщення штовхальника, визначають, використовуючи метод повернення руху, відповідно до якого, всій системі, включаючи стійку, уявно повідомляють рух з кутовою швидкістю (ω1).Тоді в зверненому русі кулачок стає нерухомим: ω*1 = ω1 + (–ω1) = 0, а вісь штовхальника разом зі стійкою будуть переміщатися в напрямку (–ω1). І кут повороту кулачка, що відповідає тій чи іншій фазі руху, визначається по куту повороту осі штовхальника в зверненому русі на відповідній ділянці. Вісь штовхальника в зверненому русі в будь-якому положенні буде стосуватися окружності радіуса rе.
Поворот кулачка на ділянці:
01 – φ01 12 – φ12 23 – φ23
робочий кут повороту кулачка φраб:
φраб = φ01 + φ12 + φ23
(уб) (выс) (сб)
Завжди незалежно від схеми механізму φраб = ψраб, а
φуд ≠ ψуд, φвыс ≠ ψвыс, φсб ≠ ψсб,
для всіх схем, крім кулачкового механізму з центральним штовхальником.
Похожие работы
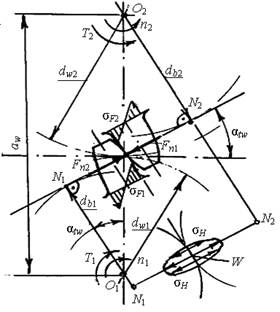
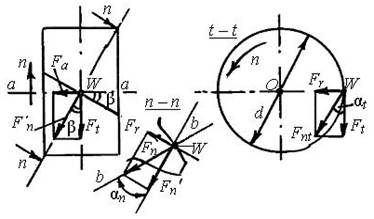
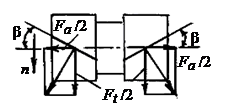
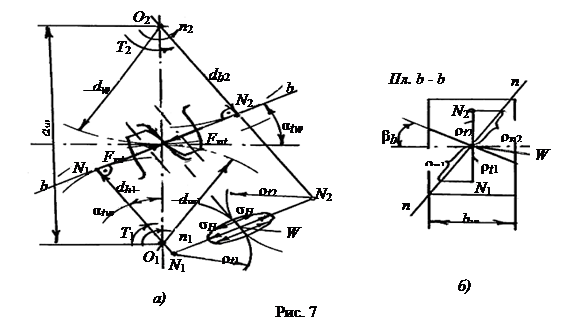
... колес нарезают тем же инструментом, что и прямые, установленным относительно заготовки под углом β. Расчет на прочность принято вести для прямозубой передачи. Для этого все зубчатые и червячные передачи приводятся к эквивалентным прямозубым цилиндрическим. Эквивалентные параметры косозубого цилиндрического колеса (приведение рассматривалось в курсе "Теория машин и механизмов"): делительный ...
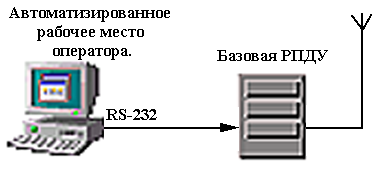
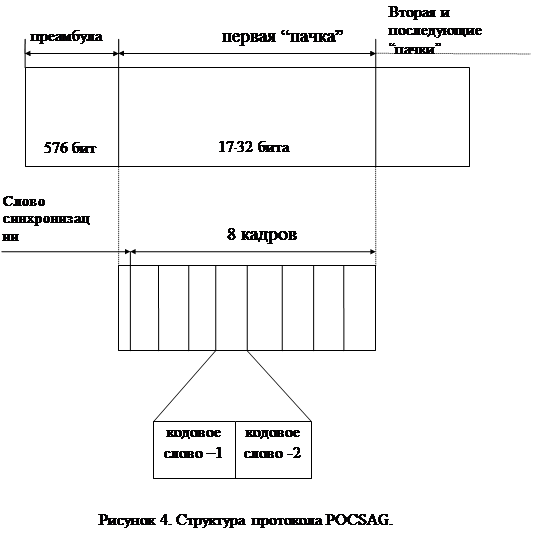
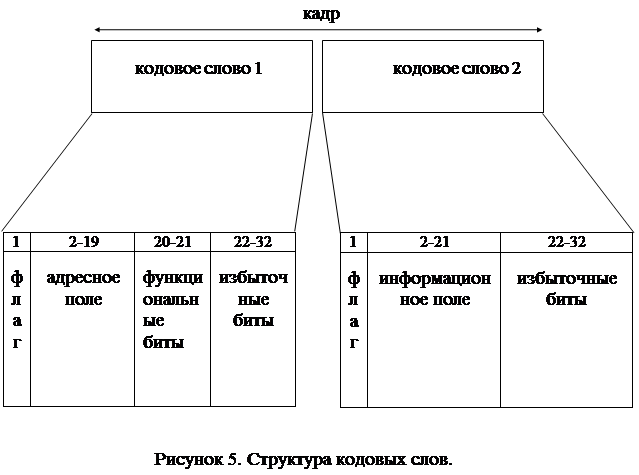
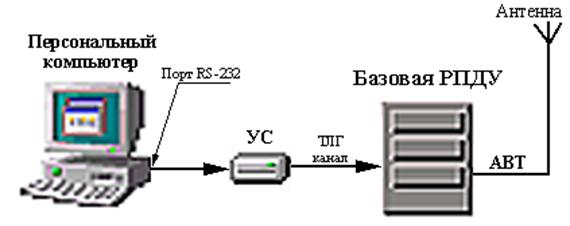
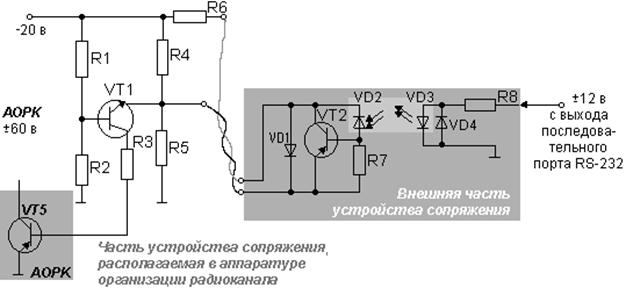
... указания. 1 Цель: 1.1 Изучить наиболее распространенные стандарты систем персонального радиовызова общего пользования. 2 Литература: 2.1 Соловьёв А. А., Смирнов С. И. Техническая энциклопедия пейджинговой связи. Эко-Трендс М:, 1998 стр. 18-50. 2.2 Громов Ю. А. Стандарты и системы подвижной радиосвязи. Эко-Трендс М:, 1998 стр. 39-52 2.3 Приложение к ...
... 195.7 9 2 25.47 392.6 8.49 4 1.3 60.81 164.4 10 2 30.33 329.7 10.11 I - - 76 131.6 I I I 8 1.68 36.09 277.1 12.03 9 1.42 42.96 232.8 14.32 2. Расчет цепной передачи 2.1. Передаточное число передачи u = 3 2.2. Принимаем число зубьев для ведущей звездочки Z1= 25 таб. 11.4 [1] тогда ...
... Направление линии зуба правое. Вращение против часовой стрелки. при bm=35° при bm=35° Направление линии зуба левое. Вращение по часовой стрелке. 7. РАСЧЁТ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ 7.1 Выбор материалов червяка и червячного колеса Для изготовления червяков применяют углеродистые и легированные стали (см. табл. 3.1). Выбор марки стали зависит от назначаемой термообработки ...



0 комментариев