Навигация
Основные понятия математического анализа
Содержание
Двойные интегралы
Определение определенного интеграла
Правило вычисления двойного интеграла.
Вычисление объемов тел с помощью двойного интеграла
Вычисление площадей поверхностей фигур с помощью двойного интеграла.
Тройные интегралы
Вычисление объемов тел с помощью тройного интеграла.
Несобственные интегралы.
Дифференциальные уравнения.
1. Дифференциальные уравнения первого порядка с разделяющимися переменными
2. Однородные дифференциальные уравнения первого порядка
3. Линейные дифференциальные уравнения
4. Уравнения Бернулли
Дифференциальные уравнения второго порядка.
Три случая понижения порядка.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Комплексные числа
Геометрическое изображение комплексных чисел
Действия над комплексными числами.
Произведение.
Частное.
Возведение в степень.
Извлечение корня
Ряды.
Числовые ряды.
Свойства числовых рядов.
Знакоположительные ряды
Признаки сходимости и расходимости знакоположительных рядов.
Знакопеременные и знакочередующиеся ряды.
ДВОЙНЫЕ ИНТЕГРАЛЫ
Определение определенного интеграла
![]() - интегральная сумма.
- интегральная сумма.
![]()
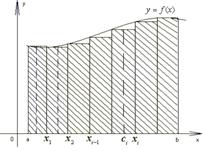
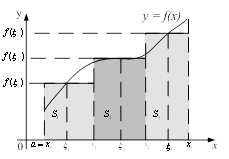
Геометрический смысл ОИ: равен площади криволинейной трапеции.
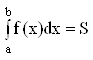
Аналогично ОИ выводится и двойной интеграл.
Пусть задана функция двух переменных z=f(x,y), которая определена в замкнутой области S плоскости ХОУ.
Интегральной суммой для этой функции называется сумма
![]()
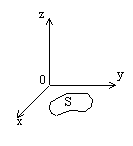
Она распространяется на те значения i и к, для которых точки (xi,yk) принадлежат области S.
Двойной интеграл от функции z=f(x,y), определенной в замкнутой области S плоскости ХОУ, называется предел соответствующей интегральной суммы.
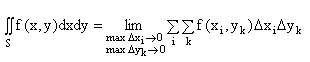
Правило вычисления двойного интеграла
Двойной интеграл вычисляется через повторные или двукратные интегралы. Различаются два основных вида областей интегрирования.
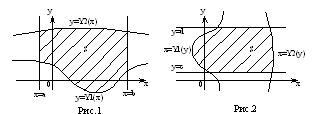
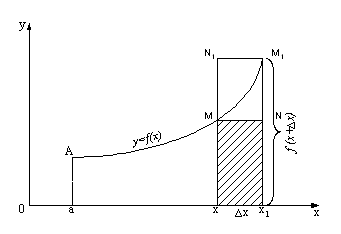
1. (Рис.1) Область интегрирования S ограничена прямыми х=а, х=в и кривыми
![]() .
.
Для такой области двойной интеграл вычисляется через повторный по формуле:
![]()
Сначала вычисляется внутренний интеграл:
При вычислении внутреннего интеграла ‘у’ считается переменной, а ‘х’-постоянной.
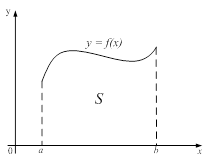
2. (Рис.2) Область интегрирования S ограничена прямыми у=С, у=d и кривыми
![]() .
.
Для такой области двойной интеграл вычисляется через повторный по формуле:
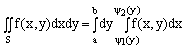
Сначала вычисляется внутренний интеграл, затем внешний.
При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной.
3. Если область интегрирования не относится ни к 1 ни ко второму случаю, то разбиваем ее на части таким образом, чтобы каждая из частей относилась к одному из этих двух видов.
Вычисление объемов тел с помощью двойного интеграла
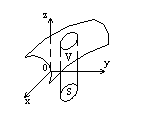
Объем тела, ограниченного сверху поверхностью z=f(x,y), снизу- плоскостью z=0 (плоскость ХОУ) и с боков- цилиндрической поверхностью, вырезающей на плоскости ХОУ область S, вычисляется по формуле:
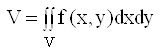
Вычисление площадей поверхностей фигур с помощью двойного интеграла
Если гладкая поверхность задана уравнением z=f(x,y), то площадь поверхности (Sпов.), имеющей своей проекцией на плоскость ХОУ область S, находится по формуле:
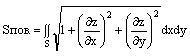 - площадь поверхности.
- площадь поверхности.
ТРОЙНЫЕ ИНТЕГРАЛЫ
Определяется аналогично двойному интегралу.
Тройной интеграл от функции U=f(x,y,z), распространенным на область V, называется предел соответствующей трехкратной суммы.
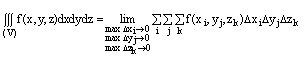
Вычисление тройного интеграла сводится к последовательному вычислению обыкновенных (однократных) нтегралов.
Вычисление объемов тел с помощью тройного интеграла
Объем тела вычисляется по формуле:
![]()
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Это интегралы: - с бесконечными пределами; - от неограниченной функции.
Первый вид
Несобственные интегралы с бесконечными пределами имеют вид:
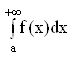 ;
; 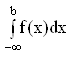 ;
; 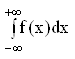
Несобственные интегралы от функции в пределах от (а) до (![]() ) определяются равенством.
) определяются равенством.
1.![]() ; 2.
; 2. ![]() ; 3.
; 3. 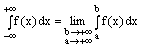
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся (ряд сходится или расходится?). Это и есть ответ.
Второй вид
Несобственные интегралы от неограниченной функции имеют вид: ![]() , где существует точка “с” (точка разрыва) такая, что
, где существует точка “с” (точка разрыва) такая, что ![]() ;
; ![]() , т.е.
, т.е. ![]() (в частности c=a; c=b).
(в частности c=a; c=b).
Если функция f(x) имеет бесконечный разрыв в точке “с” отрезка [a;b] и непрерывна при ![]() или
или ![]() , то полагаем:
, то полагаем: ![]()
Если пределы в правой части последнего равенства существуют и конечны, то несобственный интеграл сходится, если пределы не существуют или равны бесконечности - то расходятся.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Похожие работы
... некая иерархическая структура. Третья идея ССА широкое использование графических нотаций, что облегчает понимание сложных систем. В результате можно дать следующее определение ССА: структурным системным анализом называется метод исследования, проектирования и описания сложных систем в виде иерархии "черных ящиков" с помощью графических средств. Другие принципы ССА Методология ССА строится ...
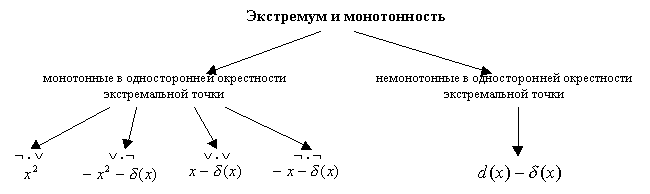
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
... Итак, работа переменной силы , величина которой есть непрерывная функция F = F(x), действующая на отрезке [a; b], равна определенному интегралу от величины F(x) силы, взятому по отрезу [a; b]. В этом состоит механический смысл определенного интеграла. Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t = a до t = b, равен определенному интегралу от скорости v(t): ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
0 комментариев