Навигация
Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные
1. Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные .
Символически дифференциальное уравнение выглядит:
F(x,y,y’,y’’…,y(n))=0 или ![]() .
.
2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение:
Пример.
F(x,y,y’)=0- дифференциальное уравнение первого порядка.
F(x,y,y’,y’’)=0- дифференциальное уравнение второго порядка.
3. Решением дифференциального уравнения называется всякая функция ![]() , которая при подстановке в уравнение, обращает его в верное тождество.
, которая при подстановке в уравнение, обращает его в верное тождество.
Для того чтобы решить дифференциальное уравнение надо его проинтегрировать.
Пример.
Дифференциальное уравнение первого порядка.
Общее и частное решения.
F(x,y,y’)=0
Это уравнение можно привести к виду y’=f(x,y).
Интегрируем уравнение.
После вычисления возникает постоянная С. Поэтому решение фактически зависит не только от х, но и от С, т.е. y=f(x,C). Придавая С различные значения, мы получаем множество различных решений дифференциального уравнения. Эти решения (y=f(x,C)) называются общим решением дифференциального уравнения.
Придавая С различные значения получаем различные решения дифференциального уравнения. Так как С имеет бесконечное множество значений, то и решений будет бесконечное множество (которые отличаются друг от друга путем сдвига на несколько единиц).
Геометрически общее решение представляет собой семейство кривых на координатной плоскости ХОУ.
Частное решение.
Пусть в дифференциальном уравнении заданы дополнительные условия, что при х=х0 функция принимает значение у=у0. Это дополнительное условие называется начальным условием и записывается: а). у=у0 при х=х0; б). ![]() ; в). у(х0)=у0.
; в). у(х0)=у0.
Геометрически начальное условие означает некоторую точку (х0,у0) на плоскости ХОУ.
Подставляя ![]() в начальное условие
в начальное условие ![]() , находим вполне определенные значения постоянной С. Тогда
, находим вполне определенные значения постоянной С. Тогда ![]() является частным решением уравнения.
является частным решением уравнения.
Геометрически частное решение обозначает: начальное условие задает некоторую точку на плоскости и из семейства кривых (общее решение) выбирается та единственная кривая, которая проходит через эту точку.
Теорема существования и единственности решения дифференциального уравнения (теорема Коши).
Если в дифференциальном уравнении y=f(x,y) функция f(x,y) и ее частная производная ![]() определены и непрерывны в некоторой области Д на плоскости ХОУ, то какова бы ни была внутренняя точка (х0,у0) этой области, данное уравнение имеет единственное решение
определены и непрерывны в некоторой области Д на плоскости ХОУ, то какова бы ни была внутренняя точка (х0,у0) этой области, данное уравнение имеет единственное решение ![]() , удовлетворяющее начальному условию у=у0 при х=х0.
, удовлетворяющее начальному условию у=у0 при х=х0.
Геометрически смысл заключается в следующем: каждой точке (х0,у0) области Д соответствует только одна интегральная кривая, проходящая через эту точку (каждой точке соответствует только одно частное решение).
Замечание. “Найти частное решение”=“Решить задачу Коши”.
Существует 4 вида дифференциальных уравнений первого порядка.
1. Дифференциальные уравнения первого порядка с разделяющимися переменными.
Дифференциальные уравнения первого порядка в общем виде можно записать либо через производные F(x,y,y’)=0, либо через дифференциалы
![]() .
.
Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде:
- ![]() - через производную.
- через производную.
- ![]() - через дифференциал.
- через дифференциал.
В этих уравнениях в произведениях стоят функции, каждая из которых зависит от одной переменной (х или у). Т.е. уравнение будет уравнением с разделяющимися переменными, если его можно преобразовать так, чтобы в одной его части была только одна переменная, а в другой – только другая.
Замечание. При решении дифференциальное уравнение ответу можно придать различную форму в зависимости от того, как записана произвольная постоянная С.
Решение.
- ![]()
![]() ;
; ![]() -интегрируем и получаем решение.
-интегрируем и получаем решение. ![]()
- ![]()
![]() ;
; ![]()
Однородные дифференциальные уравнения первого порядка
Функция f(x,y) называется однородной функцией n–го измерения, если при любом ![]() выполняется условие:
выполняется условие: ![]() .
.
Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.
P(x,y)dx=-Q(x,y)dy; ![]()
Однородное уравнение всегда можно привести к виду ![]() и с помощью замены
и с помощью замены ![]() однородное уравнение всегда приводится к уравнению с разделяющимися переменными (
однородное уравнение всегда приводится к уравнению с разделяющимися переменными (![]() ; y=xt; y’=t+xt’).
; y=xt; y’=t+xt’).
Линейные дифференциальные уравнения
ЛДУ- уравнения вида y’+P(x)y=Q(x)– первого порядка относительно у и у’.
Для решения ЛДУ применяем замену: y=UV, тогда y’=U’V+UV’
U’V+UV’+P(x)UV=Q(x)
V(U’+P(x)U)+UV’=Q(x)
Далее U’+P(x)U=0, получаем два уровнения с разделяющимися переменными:
1). U’+P(x)U=0 находим U. ![]() 2). UV’=Q(x) находим V.
2). UV’=Q(x) находим V. ![]() . С ставится только при вычислении второго уравнения.
. С ставится только при вычислении второго уравнения.
Замечание. Выражение, стоящее в скобках, можно прировнять к нулю, т.к. одну из функций можно взять произвольной, другую – определяем на основании ЛДУ.
Уравнения Бернулли
УБ- дифференциальные уравнения вида y’+P(x)y=Q(x)*yn, где
![]() - т.к. при этих значениях уравнение будет линейным.
- т.к. при этих значениях уравнение будет линейным.
УБ решаются так же, как и линейные.
Дифференциальные уравнения второго порядка
Дифференциальные уравнения второго порядка в общем виде записываются: F(x,y,y’,y’’)=0
Как и в случае дифференциальных уравнений первого порядка для решения дифференциальных уравнений второго порядка существуют общее и частное решения. Но, если для дифференциальных уравнений первого порядка решение зависело от одной константы С, то для дифференциальных уравнений второго порядка решение зависит от двух постоянных: ![]() - общее решение.
- общее решение.
Если заданы начальные условия (у=у0, у=у0 при х=х0), то получаем частное решение, удовлетворяющее этим начальным условиям.
Начальные условия так же могут задаваться в виде:
у=у0 при х=х0; у=у1 при х=х1.
Три случая понижения порядка
1. Случай непосредственного интегрирования
F(x,y”)=0
y’’=f(x)- решение этого уравнения находится путем двукратного интегрирования.
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Похожие работы
... некая иерархическая структура. Третья идея ССА широкое использование графических нотаций, что облегчает понимание сложных систем. В результате можно дать следующее определение ССА: структурным системным анализом называется метод исследования, проектирования и описания сложных систем в виде иерархии "черных ящиков" с помощью графических средств. Другие принципы ССА Методология ССА строится ...
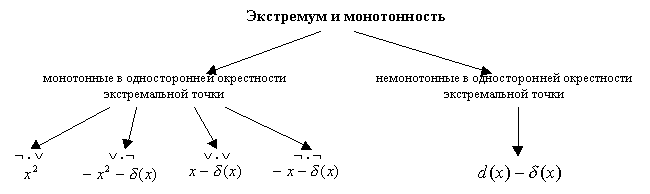
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
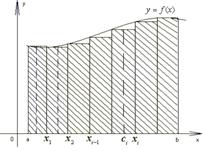
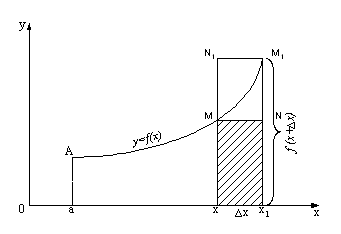
... Итак, работа переменной силы , величина которой есть непрерывная функция F = F(x), действующая на отрезке [a; b], равна определенному интегралу от величины F(x) силы, взятому по отрезу [a; b]. В этом состоит механический смысл определенного интеграла. Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t = a до t = b, равен определенному интегралу от скорости v(t): ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
0 комментариев