Навигация
Розрахунки зручно вести складаючи таку таблицю
1. Розрахунки зручно вести складаючи таку таблицю.
Розрахунки допоміжних величин для обчислення кореляції і регресії ![]() по
по ![]() .
.
| № пари | Значення ознаки |
|
|
| |
|
|
| ||||
| 1 2 3 4 5 6 7 8 9 10 11 12 Сума | 19,9 20,9 26,1 29,4 30,5 40,3 44,8 47,8 55,6 58,3 64,5 76,6
| 0,0 0,6 1,1 1,2 1,7 1,7 2,6 3,4 4,2 5,8 6,3 7,3
| 396,01 436,81 681,21 864,36 930,25 1624,09 2007,04 2284,84 3091,36 3398,89 4160,25 5867,56
| 0,00 0,36 1,21 1,44 2,89 2,89 6,76 11,56 17,64 33,64 39,69 53,29
| 0,00 12,54 28,71 35,28 51,85 68,51 116,48 162,52 233,52 338,14 406,35 559,18
|
Розв’язання:
2. За даними таблиці обчислюємо шість допоміжних величин: ![]() ;
;
![]()
![]()
![]()
![]()
![]()
3. Обчислюється коефіцієнт кореляції, регресії і рівняння регресії:
коефіцієнт кореляції
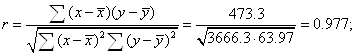
коефіцієнт регресії ![]() і
і ![]()
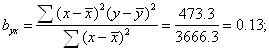
Рівняння регресії
![]()
Таким чином шукана залежність має вигляд: ![]()
4. Визначається похибка і критерій значущості для коефіцієнта кореляції:
Похибка коефіцієнта кореляції
![]()
критерій значущості коефіцієнта кореляції
![]()
5. Фактичне значення ![]() порівнюється з теоретичним
порівнюється з теоретичним ![]() , яке приймається рівним: 8-9 ступенів волі (при
, яке приймається рівним: 8-9 ступенів волі (при ![]() - це 10-11 пар спостережень) – 2,3; для 10-14 ступенів волі – 2,2; для 15-24 ступенів волі – 2,1; для 25-100 ступенів волі – 2,0. Кореляція і регресія визначається суттєвою, якщо
- це 10-11 пар спостережень) – 2,3; для 10-14 ступенів волі – 2,2; для 15-24 ступенів волі – 2,1; для 25-100 ступенів волі – 2,0. Кореляція і регресія визначається суттєвою, якщо ![]() . В нашому прикладі
. В нашому прикладі ![]() , так як
, так як ![]() . Значить між вологістю грунту і її налипання є суттєвий прямий зв’язок.
. Значить між вологістю грунту і її налипання є суттєвий прямий зв’язок.
6. За отриманим рівнянням регресії обчислюють теоретичне значення ![]() для крайніх величин
для крайніх величин ![]() (19,9 і 76,6, згідно таблиці)
(19,9 і 76,6, згідно таблиці)
![]() ;
;
![]()
Знайдені точки (![]()
![]() і
і![]()
![]() ) наносяться на графіці, з’єднуючи їх прямою, маємо теоретичну лінію регресії. Вона показує, що збільшення вологості грунту на 1% відповідає збільшенню налипання на 0,13 г/см2.
) наносяться на графіці, з’єднуючи їх прямою, маємо теоретичну лінію регресії. Вона показує, що збільшення вологості грунту на 1% відповідає збільшенню налипання на 0,13 г/см2.
Парна залежність може бути апроксимована прямою лінією, параболою, гіперболою, логарифмічною, степеневою або показниковою функцією,поліномом і інше.
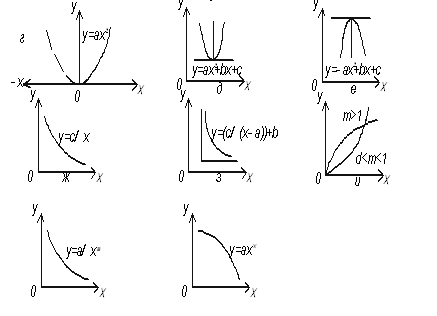
Рис. Вигляди основних ліній різних зв’язків між змінними величинами і їх рівняння.
1. Пряма, яка проходить через початок координат має рівняння ![]() (3,а).
(3,а).
2. Пряма, що не проходить через початок координат має рівняння ![]() , або
, або ![]() . Ці залежності вимагають визначення двох параметрів
. Ці залежності вимагають визначення двох параметрів ![]() і
і ![]() . (3, б, в).
. (3, б, в).
3. Парабола з вершиною в початку координат і симетрична одній із осей має рівняння ![]() . Формула один параметр
. Формула один параметр ![]() із зменшенням якого зменшується розхил параболи (рис.3, г).
із зменшенням якого зменшується розхил параболи (рис.3, г).
4. Парабола, симетрична прямій паралельній осі ![]() має рівняння
має рівняння ![]() . Функція квадратична. У формулі необхідно визначити три параметра:
. Функція квадратична. У формулі необхідно визначити три параметра: ![]() ,
, ![]() і
і ![]() (рис.3, д, є).
(рис.3, д, є).
5. Гіпербола, асимптотично наближається до осей координат, рівняння має вигляд ![]() , необхідно визначити параметр
, необхідно визначити параметр ![]() (рис.3, ж).
(рис.3, ж).
6. Гіпербола асимптотично наближається до прямих, паралельних до осей координат, рівняння має вигляд ![]() . Параметри
. Параметри ![]() і
і ![]() є координатами точки
є координатами точки ![]() . Знак параметра
. Знак параметра ![]() залежить від розміщення гіперболи по відношенню до асимптот (рис.3, з).
залежить від розміщення гіперболи по відношенню до асимптот (рис.3, з).
7. Степеневі криві (рис.3, и, к), рівняння ![]() , де
, де ![]() може бути додатнім, цілим або дробовим.
може бути додатнім, цілим або дробовим.
8. Показникові крива, коли із зростанням однієї величини ![]() спостерігається підсилене зростання
спостерігається підсилене зростання ![]() . Рівняння
. Рівняння ![]() (рис.8.3, л).
(рис.8.3, л).
Двох факторне поле можна апроксимувати, площиною, параболоїдом другого порядку, гіперболоїдом. Для ![]() - змінних фактів зв’язок можна встановити за допомогою
- змінних фактів зв’язок можна встановити за допомогою ![]() - мірного простору рівняннями другого порядку
- мірного простору рівняннями другого порядку
 (17)
(17)
де ![]() - функція мети багатофакторних змінних;
- функція мети багатофакторних змінних;
![]() - незалежні фактори;
- незалежні фактори;
![]() - коефіцієнт регресії, що характеризують вплив фактора
- коефіцієнт регресії, що характеризують вплив фактора ![]() на функцію мети;
на функцію мети;
![]() - коефіцієнти, які характеризують подвійний вплив факторів
- коефіцієнти, які характеризують подвійний вплив факторів ![]() і
і ![]() на функцію мети.
на функцію мети.
При побудові теоретичної регресійної залежності, оптимальною буде така функція, в якій виконуються умови найменших квадратів ![]() , де
, де ![]() - фактичні координати поля;
- фактичні координати поля; ![]() - середнє значення ординати з абсцисою
- середнє значення ординати з абсцисою ![]() , обчисленою з рівняння. Після кореляції апроксимують рівнянням прямої. Лінію регресії розраховують з умови найменших квадратів:
, обчисленою з рівняння. Після кореляції апроксимують рівнянням прямої. Лінію регресії розраховують з умови найменших квадратів:
![]() (18)
(18)
При цьому крива АВ найкращим чином вирівнює значення постійних коефіцієнтів ![]() і
і ![]() , тобто коефіцієнтів рівняння регресії. Їх обчислюють за формулами:
, тобто коефіцієнтів рівняння регресії. Їх обчислюють за формулами:
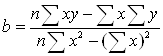 (19)
(19)
![]() (20)
(20)
Критерієм близькості кореляційної залежності між ![]() і
і ![]() до лінійної функціональної залежності є коефіцієнт парної або просто коефіцієнт кореляції
до лінійної функціональної залежності є коефіцієнт парної або просто коефіцієнт кореляції ![]() . Він просто показує ступінь лінійності зв’язку
. Він просто показує ступінь лінійності зв’язку ![]() і
і ![]() .
.
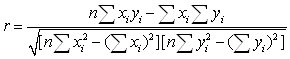 (21)
(21)
де ![]() - число вимірів.
- число вимірів.
Задовільна тіснота зв’язку при ![]() , добра при
, добра при ![]() . Для визначення проценту мінливості шуканої функції
. Для визначення проценту мінливості шуканої функції ![]() відносно її середнього значення, який визначається мінливістю фактора
відносно її середнього значення, який визначається мінливістю фактора ![]() , обчислюють коефіцієнт детермінації
, обчислюють коефіцієнт детермінації
![]() (22)
(22)
Рівняння регресії прямої записати таким виразом:
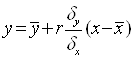 (23)
(23)
Література:
1. Белый И.В. и др. Основы научных исследований и технического творчества / И.В. Белый, К.П. Власов, В.Б. Клепиков. — Х,: Вища шк. Изд-во при Харьк. ун-те, 1989-200с.
2. Белуха Н.Т. Основы научных исследований в экономике. — К.: Вища шк. Головное изд-во, 1985.— 215с.
3. Вознюк С.Т. и др. Основы научных исследований. Гидромелиорация / Вознюк С.Т., Гончаров С.М., Ковалев С.В. — К.: Вища шк. Головное издательство, 1985-192с.
4. Воловик П.М. Теорія імовірностей і математична статистика в педагогіці —Х.: Вища шк., 1969-222с.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. Изд. 4-е — М.: Высшая школа, 1972. — 367с.
6. Митропольский А.К. Техника статистических вычислений. М.: Наука, 1971, 576с.
7. Нечаев Ю.И. Основы научных исследований — Киев, Одесса: Вища шк. Головное изд-во, 1983, — 160с.
8. Румшиский Л.Э. Математическая обработка результатов эксперимента. М.: Наука, 1971,— 192с.
9. Сиденко В.М. Грушко И.М. Основы научных исследований. Харьков. Вища шк, 1977, — 240с.
10. Сытник В.Ф. Основы научных исследований. К.: Вища шк. Головное изд-во. 1978, — 184с.
Похожие работы
... одних характеристик при варіюванні інших. Проте, такі експерименти не завжди повністю моделюють хід процесу, що вивчається. Педагогічні експериментальні дослідження Педагогічний експеримент є своєрідним комплексом методів дослідження, який забезпечує науково- об’єктивну і доказову перевірку, правильно обґрунтованої на початку дослідження, гіпотези. Він дозволяє перевірити ефективність тих ...
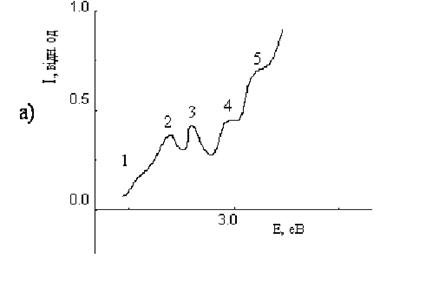
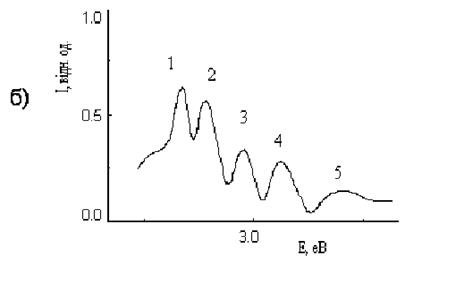
... можливо зробити висновок про склад смуг у вихідному спектрі і розрахувати їх. У статті [7] автори зіштовхнулися із завданням одержання інформації про поводження індивідуальних смуг фотолюмінесценції при пластичній деформації кристалів ZnS:Mn і випробували деякі з методів, особливо методи: Аленцева-Фока, метод імпульсного збудження зразків. Так само автори запропонували свій метод розкладання. У ...
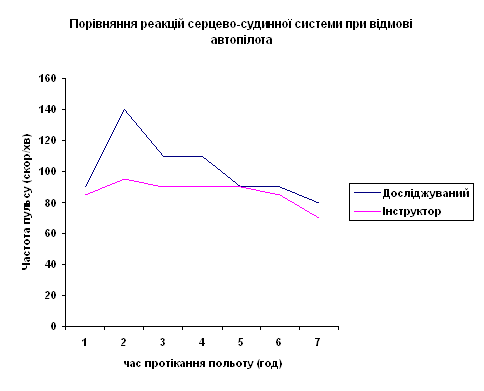
... Пілот літального апарату являється оператором складної технічної системи і його діяльність часто протікає в особливих умовах. Психологічна проблема формування спеціальних навичок і вмінь, так же як проблема вдосконалення аварійної сигналізації, визначена аналізом поведінки пілотів в процесі неочікуваного виникнення ускладнень в польоті. Різниця ступеня готовності пілотів успішно діяти в авар ...
... введемо в останню формулу її оцінку , звідки дисперсія буде: (2.2) Таким чином, середнє значення лежить у межах: (2.3) Розділ ІІІ. Лінійний регресійний аналіз інтервальних даних Перейдемо до багатомірного статистичного аналізу. Спочатку з позиції асимптотичної математичної статистики інтервальних даних розглянемо оцінки методу найменших квадратів (МНК). Статистичне дослідження ...

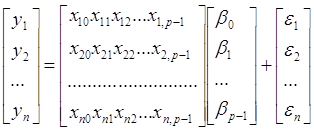
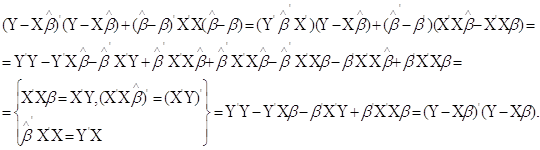
0 комментариев