Навигация
Формули приведення для Беселевих функцій
2. Формули приведення для Беселевих функцій
Маємо:
![]() ;
; ![]() ;
;
![]() ,
, ![]() ;
;
![]() .
.
Отже,
![]() . (10)
. (10)
Таким чином, операція ![]() (що складається в диференціюванні з наступним множенням на
(що складається в диференціюванні з наступним множенням на ![]() ), застосована до
), застосована до ![]() , підвищує в цьому вираженні індекс
, підвищує в цьому вираженні індекс ![]() на одиницю й міняє знак. Застосовуючи цю операцію
на одиницю й міняє знак. Застосовуючи цю операцію ![]() раз, де
раз, де ![]() – будь-яке натуральне число, одержуємо:
– будь-яке натуральне число, одержуємо:
![]() . (10`)
. (10`)
Маємо:
![]() ;
;

Отже,
![]() . (11)
. (11)
Таким чином, операція ![]() , застосована до
, застосована до ![]() , знижує в цьому вираженні індекс
, знижує в цьому вираженні індекс ![]() на одиницю. Застосовуючи цю операцію
на одиницю. Застосовуючи цю операцію ![]() раз, одержуємо:
раз, одержуємо:
![]() . (11`)
. (11`)
З виведених формул можна одержати деякі наслідки. Використовуючи (10), одержимо:
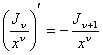 ;
; ![]() ;
; ![]() .
.
Звідси, зокрема, треба, що ![]() . Використовуючи (11), одержимо:
. Використовуючи (11), одержимо:
![]() ;
; ![]() ;
; ![]() .
.
По членне додавання й вирахування отриманих рівностей дає:
![]() , (12)
, (12)
![]() . (13)
. (13)
Формула (13) дозволяє виразити всі Беселеві функції із цілими індексами через ![]() ,
, ![]() . Дійсно, з (13) знаходимо (думаючи
. Дійсно, з (13) знаходимо (думаючи ![]() ):
):
![]() , (13`)
, (13`)
звідки послідовно одержуємо:
![]() ,
,
![]() , …………………
, …………………
3. Беселеві функції з напівцілим індексом
Беселеві функції, загалом кажучи, є новими трансцендентними функціями, що не виражаються через елементарні функції. Виключення становлять Беселеві функції з індексом ![]() , де
, де ![]() – ціле. Ці функції можуть бути виражені через елементарні функції.
– ціле. Ці функції можуть бути виражені через елементарні функції.
Маємо:
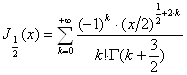 ,
,
![]() ,
,
отже,
 .
.
Але ![]() , значить:
, значить:
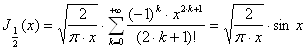 . (14)
. (14)
Далі
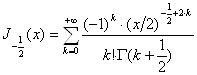 ,
,
![]() ,
,
отже,
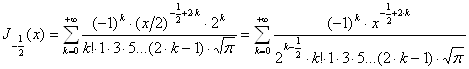 .
.
Але ![]() , тому
, тому
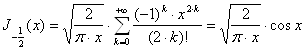 . (15)
. (15)
За допомогою (10') знаходимо:
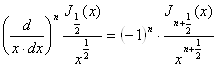 ,
,
а з огляду на (14)
 ,
,
отже, при цілому позитивному ![]()
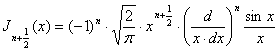 . (14`)
. (14`)
За допомогою (11') знаходимо:
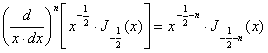 ,
,
але в силу (15)
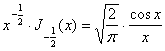 ,
,
і, отже, при цілому позитивному ![]()
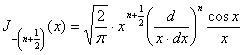 . (15`)
. (15`)
4. Інтегральне подання Беселевих функцій із цілим індексом
Виробляюча функція системи функцій
Розглянемо систему ![]() функцій
функцій ![]() (з будь-якою загальною областю визначення), пронумерованих за допомогою всіх цілих чисел:
(з будь-якою загальною областю визначення), пронумерованих за допомогою всіх цілих чисел:
![]()
Складемо ряд
![]() ,
,
де ![]() – комплексна змінна. Припустимо, що при кожному
– комплексна змінна. Припустимо, що при кожному ![]() (приналежному області визначення розглянутих функцій) цей ряд має кільце збіжності, що містить усередині себе одиничну окружність
(приналежному області визначення розглянутих функцій) цей ряд має кільце збіжності, що містить усередині себе одиничну окружність ![]() . Зокрема, це кільце може являти собою повну площину комплексної змінної без крапок 0 і?.
. Зокрема, це кільце може являти собою повну площину комплексної змінної без крапок 0 і?.
Функція
![]() (16)
(16)
(де x лежить в області визначення функцій системи ![]() ,
, ![]() – усередині кільця збіжності, що відповідає розглянутому значенню
– усередині кільця збіжності, що відповідає розглянутому значенню ![]() ) називається виробляючою функцією системи
) називається виробляючою функцією системи ![]() .
.
Обернено, нехай задана функція ![]() , де
, де ![]() пробігає деяку множину,
пробігає деяку множину, ![]() перебуває усередині деякого кільця, що залежить від
перебуває усередині деякого кільця, що залежить від ![]() , із центром 0 і утримуючого усередині себе одиничну окружність. Тоді, якщо
, із центром 0 і утримуючого усередині себе одиничну окружність. Тоді, якщо ![]() при кожному
при кожному ![]() аналітичне відносно
аналітичне відносно ![]() усередині відповідного кільця, тобто
усередині відповідного кільця, тобто ![]() виробляюча функція деякої системи
виробляюча функція деякої системи ![]() функцій. Справді, розклавши при кожному
функцій. Справді, розклавши при кожному ![]() функцію
функцію ![]() в ряд Лорана по ступенях
в ряд Лорана по ступенях ![]() :
:
![]() ,
,
знайдемо, що система коефіцієнтів ![]() цього ряду буде шуканою системою
цього ряду буде шуканою системою ![]() .
.
Формули для коефіцієнтів ряду Лорана дозволяють виразити функції ![]() розглянутої системи через виробляючу функцію. Застосовуючи ці формули й перетворюючи потім інтеграл уздовж одиничної окружності
розглянутої системи через виробляючу функцію. Застосовуючи ці формули й перетворюючи потім інтеграл уздовж одиничної окружності ![]() в простий інтеграл, одержимо:
в простий інтеграл, одержимо:
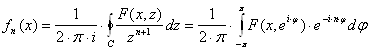 . (17)
. (17)
Виробляюча функція системи Беселевих функцій із цілими індексами
Покажемо, що для системи Беселевих функцій першого роду із цілими індексами ![]() (
(![]() …) виробляюча функція є:
…) виробляюча функція є:
![]() .
.
Маємо:
![]() ,
, ![]() ,
,
звідки після по членного перемножування цих рівностей знайдемо:

(тому що в передостанній внутрішній сумі ![]() й
й ![]() були зв'язані залежністю
були зв'язані залежністю ![]() , то ми могли покласти
, то ми могли покласти ![]() , одержавши підсумовування по одному індексі
, одержавши підсумовування по одному індексі ![]() ). В останній внутрішній сумі підсумовування виробляється по всіх цілих
). В останній внутрішній сумі підсумовування виробляється по всіх цілих ![]() , для яких
, для яких ![]() , отже, при
, отже, при ![]() це буде
це буде ![]() ; при
; при ![]() це буде
це буде ![]() . Таким чином, у всіх випадках внутрішня сума є
. Таким чином, у всіх випадках внутрішня сума є ![]() в силу формул (5`) і (5```). Отже,
в силу формул (5`) і (5```). Отже,
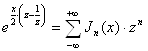 , (18)
, (18)
але це й доводить, що ![]() є виробляюча функція для системи
є виробляюча функція для системи ![]() .
.
Виведемо деякі наслідки з формули (18). Думаючи в ній ![]() , одержимо:
, одержимо:
![]() ,
,
звідки після поділу дійсної й мнимої частини (з огляду на, що ![]() )
)
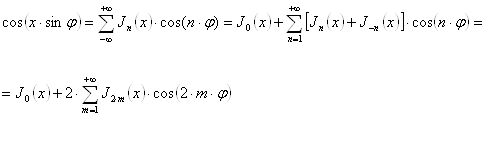 (18`)
(18`)
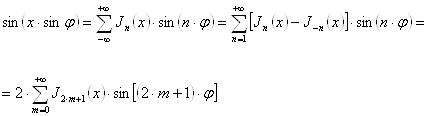 (18``)
(18``)
Заміняючи в (18`) і (18``) ![]() на
на ![]() , знайдемо:
, знайдемо:
![]() , (18```)
, (18```)
![]() . (18````)
. (18````)
Інтегральне подання Jn(x)
Тому що, по доведеному, при ![]() маємо
маємо ![]() , те по формулі (17) одержуємо (використовуючи в перетвореннях формули Ейлера):
, те по формулі (17) одержуємо (використовуючи в перетвореннях формули Ейлера):

де прийнято в увагу, що ![]() є парна функція від
є парна функція від ![]() є непарна функція від
є непарна функція від ![]() . Отже, доведено, що для будь-якого цілого числа
. Отже, доведено, що для будь-якого цілого числа ![]()
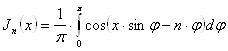 . (19)
. (19)
Формула (19) дає подання Беселевих функцій із цілим індексом у вигляді певного інтеграла, що залежить від параметра ![]() . Ця формула називається інтегральним поданням Беселя для
. Ця формула називається інтегральним поданням Беселя для ![]() , права частина формули називається інтегралом Беселя. Зокрема, при
, права частина формули називається інтегралом Беселя. Зокрема, при ![]() знайдемо:
знайдемо:
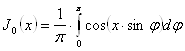 . (19`)
. (19`)
0 комментариев