Ряди Фур'є-Беселя

5. Ряди Фур'є-Беселя

Розглянемо на якому-небудь інтервалі  (кінцевому або нескінченному) два диференціальних рівняння

, , (20)

де  й  – безперервні функції на . Нехай  і  – ненульові рішення цих рівнянь. Множення на  й на  й наступне вирахування дають

.

Нехай  і  належать  і , тоді після інтегрування в межах від  до  одержимо

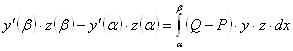. (21)

Якщо  й  – сусідні нулі рішення , то між  і   зберігає постійний знак, нехай, наприклад,  на (, ) (у противному випадку варто замінити  на ), тоді ,  (рівність нулю виключено, тому що  – ненульове рішення диференціального рівняння другого порядку). Якщо на  , то  повинна, принаймні, раз звертатися в нуль між  і , тому що інакше  збереже постійний знак на (,). Нехай, наприклад,  на (,) (у противному випадку заміняємо  на ), і тоді з (21) одержимо протиріччя, тому що ліва частина ≤0, а права >0. У такий спосіб доведена теорема порівняння Штурму: якщо P(x)<Q(x) на розглянутому інтервалі I і якщо y і z – ненульові рішення рівнянь (20), те між кожними двома сусідніми нулями y(x) перебуває принаймні один нуль z(x).

З теореми порівняння Штурму випливають нижченаведені наслідки. Якщо  на , то кожне ненульове рішення рівняння  може мати на  не більше одного нуля (це легко бачити, якщо покласти  й взяти ). Якщо  на  (де ), то для всяких двох сусідніх нулів  і  () кожного ненульового рішення рівняння  маємо  (це легко бачити, якщо покласти , взяти  й помітити, що нулями  будуть тільки числа виду ,  ціле). Якщо  на  (де ), то для всяких двох сусідніх нулів кожного ненульового рішення рівняння  маємо  (це легко бачити, якщо покласти  й взяти ). Із сказаного випливає, що якщо  на , те для всяких двох сусідніх нулів  і  () кожного ненульового рішення рівняння  маємо .

Викладене показує, що якщо  безперервно на  й перевищує деяке позитивне число поблизу +∞, те кожне ненульове рішення  рівняння має на  нескінченно багато нулів. Якщо ще  поблизу  не звертається в нуль, то ці нулі утворять нескінченну зростаючу послідовність , що має межею +∞, а якщо, крім того, , де , те .

Розглянемо рівняння Беселя

на інтервалі . Підстановка  приводить до рівняння

.

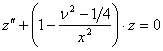Очевидно,  і  мають ті самі нулі. Тому що , де  – ціла функція, то  не має нулів на  при досить малому , і тому що  при , те при кожному  нулі  на  утворять нескінченну зростаючу послідовність

причому .

Якщо , то  задовольнить рівнянню

на інтервалі (0, +∞). Підстановка  приводить до рівняння

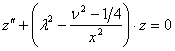
і, отже,  задовольняє цьому рівнянню. Таким чином, при будь-яких позитивних  і  маємо

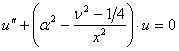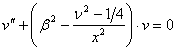, де ,

, де ,

звідки

,

отже,

, де . (22)

Нехай тепер . Розкладання  по ступенях  починається зі члена, що містить , розкладання  по ступенях  починається зі члена, що містить , тому що коефіцієнт при  дорівнює нулю, що легко бачити, виходячи з формули (5). Отже, з (22) при  одержимо

,

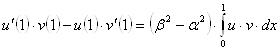тобто

, (23)

звідки видно, що якщо  і  є різними нулями функції , те

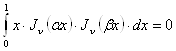. (23`)

Цим доведено, що при  система функцій

на інтервалі  є ортогональної щодо ваги .

Переходячи до межі при  в співвідношенні

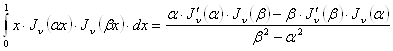
і використовуючи правило Лопиталя, одержимо при всякому

, (24)

отже, якщо  є нулем функції , те

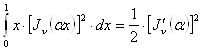. (24`)

Таким чином, при кожному  всякій безперервній функції  на , що задовольняє вимозі

,

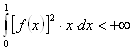поставлений у відповідність ряд Фур'є-Беселя

, (25)

коефіцієнти якого визначаються формулами

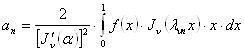. (25`)

Можна довести, що система функцій  на , ортогональна щодо ваги , замкнута. Зокрема, якщо ряд Фур'є-Беселя (25) рівномірно сходиться до його безперервної функції, що породжує.

Можна показати, що якщо  й  безперервна на  й функція, то ряд Фур'є-Беселя цієї функції сходиться до неї при .