Навигация
Интерполирование по схеме Эйткена
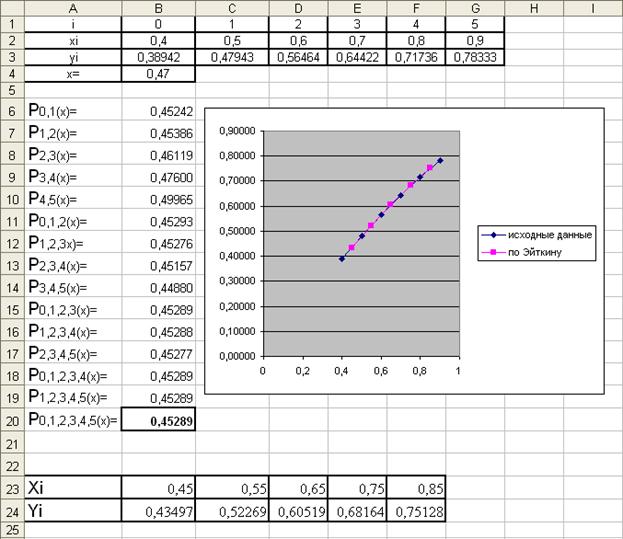
2. Интерполирование по схеме Эйткена
Итерационные методы интерполирования основаны на повторном применении некоторой простой интерполяционной схемы. Наиболее известным из итерационных методов является метод Эйткена, в основе которого лежит многократное применение линейной интерполяции.
В соответствии со схемой Эйткена линейная интерполяция по точкам Mi(xi, yi) и Mi+1(xi+1, yi+1) сводится к вычислению определителя второго порядка

При интерполировании по трем и более точкам последовательно вычисляются многочлены
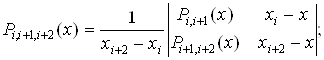
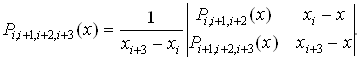
В общем случае интерполяционный многочлен n-й степени, принимающий в точках xiзначения yi (i = ![]() ), записываются следующим образом:
), записываются следующим образом:
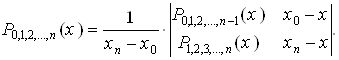
(3)
Основным достоинством схемы Эйткена является возможность постепенного увеличения числа используемых значений xi до тех пор, пока последовательные значения P0,1,2,…,n(x) и P1,2,…,n-1(x) не совпадут в пределах заданной точности. Иначе говоря, вычисления прекращаются при выполнении условия
|P0,1,2,…,n(x) - P1,2,…,n-1(x)| < e (k £ n).
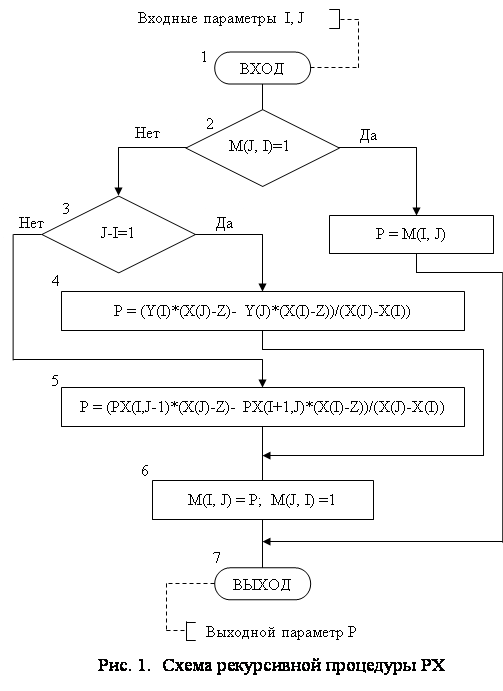
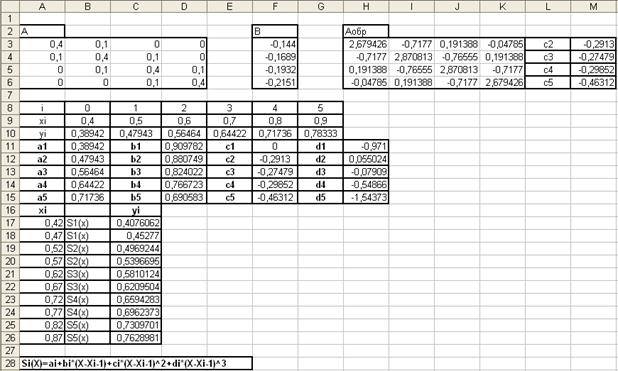
При использовании ЭВМ вычисления по формуле (3) реализуются в виде рекурсивной подпрограммы - функции РХ(I, J) с формальными параметрами I, J, определяющими индексы крайних узлов интерполирования, которые используются для получения значения соответствующего многочлена Pi,i+1,…, j (x).
Для хранения вычисленных значений P(x) используется двумерный массив M размером N*N элементов, где N - максимальное число узлов интерполирования. Каждому возможному значению P(x) соответствует один из элементов M(I, J), расположенный выше главной диагонали (I < J) и определяемый сочетанием индексов крайних узлов интерполирования.
Например, значению многочлена P1,2(x) соответствует элемент M(1,2), значению P2,3,4(x) - элемент M(2, 4) и т.д. Симметричные элементы M(J, I), расположенные ниже главной диагонали (J > I), показывают, вычислены ли соответствующие значения P(x) на данный момент, и определяются как
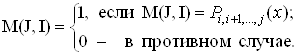
Схема рекурсивной процедуры PX приведена на рис. 1, где Х - массив значений узлов интерполирования, Y - массив значений функции в узлах интерполирования, Z - значение аргумента. Параметры X, Y, Z, M должны быть описаны как общие для главной программы и подпрограммы PX.
3. Интерполяционные формулы Ньютона для равноотстоящих узлов
Узлы интерполирования x0, x1, ..., xn называются равноотстоящими, если ![]() , где h - шаг интерполирования. При этом для некоторой функции f(x) таблично задаются значения yi = f(xi), где xi = x0 + ih.
, где h - шаг интерполирования. При этом для некоторой функции f(x) таблично задаются значения yi = f(xi), где xi = x0 + ih.
Существуют две формулы Ньютона для случая равноотстоящих узлов интерполирования, которые называются соответственно первой и второй интерполяционными формулами Ньютона и имеют вид:
![]() ;
;
![]() ,
,
В этих формулах Diyj - конечные разности, где i - порядок разности, j - ее порядковый номер, а параметры t и q определяются следующим образом:
t = (x - x0) / h; q = (x - xn) / h.
Конечные разности первого порядка вычисляются как Dyj = yj+1 – yj, где
j = ![]() , для более высоких порядков используется известная формула
, для более высоких порядков используется известная формула
![]() (i = 2, 3, ...; j =
(i = 2, 3, ...; j = ![]() ).
).
Получаемые конечные разности удобно представлять в табличной форме записи, например, в виде табл. 1, которая называется горизонтальной таблицей конечных разностей.
Таблица 1| x | y | Dy | D2y | D3y | D4y |
| x0 | Y0 | Dy0 | D2y0 | D3y0 | D4y0 |
| x1 | Y1 | Dy1 | D2y1 | D3y1 | D4y1 |
| x2 | Y2 | Dy2 | D2y2 | D3y2 | |
| x3 | Y3 | Dy3 | D2y3 | - | |
| x4 | Y4 | Dy4 | - | - | |
| x5 | Y5 | - | - | - |
Пepвая формула Ньютона применяется для интерполирования вперед и экстраполирования назад, т.е. в начале таблицы разностей, где строки заполнены и имеется достаточное число конечных разностей. При использовании этой формулы для интерполирования значение аргумента x должно лежать в интервале [x0, x1]. При этом за x0 может приниматься любой узел интерполяции xk с индексом ![]() , где m - максимальный порядок конечных разностей.
, где m - максимальный порядок конечных разностей.
Вторая формула Ньютона применяется для интерполирования назад и экстраполирования вперед, т.е. в конце таблицы конечных разностей. При этом значение аргумента x должно находиться в интервале [xn-1, xn], причем за xn может приниматься любой узел интерполирования ![]() .
.
Одно из важнейших свойств конечных разностей заключается в следующем. Если конечные разности i–го порядка (i < n) постоянны, то функция представляет собой полином i–й степени. Следовательно, формула Ньютона должна быть не выше i-й степени. При использовании ЭВМ вычисление конечных разностей завершается при выполнении условий
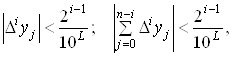
где L - число значащих цифр после запятой в представлении значений функции.
Необходимо отметить, что формулы Ньютона являются видоизменениями формулы Лагранжа. Однако в формуле Лагранжа нельзя пренебречь ни одним из слагаемых, так как все они равноправны и представляют многочлены n-й степени. В формулы Ньютона в качестве слагаемых входят многочлены повышающихся степеней, коэффициентами при которых служат конечные разности, разделенные на факториалы. Конечные разности, как правило, быстро уменьшаются, что позволяет в формулах Ньютона пренебречь слагаемыми, коэффициенты при которых становятся малыми. Это обеспечивает вычисление промежуточных значений функции достаточно точно с помощью простых интерполяционных формул.
Похожие работы
... при построении итерационных методов решения уравнения =0. Например взяв за корень линейного интерполяционного алгебраического многочлена, построенного по значениям и в узле или по значениям и в узлах и , приходят соответственно к методу Ньютона и метода секущих , где - разделенная разность функций для узлов и . Другой подход к построению численных методов решения уравнения ...
... она одновременно проходила через все точки. Поскольку приближенное уравнение изгиба пружинистого бруса имеет вид , то можно допустить, что ее форма между узлами есть алгебраический полином 3-й степени. Вероятно, интерполирующую функцию между каждыми двумя узлами можно взять, например, в таком виде: (*) . Неизвестные коэффициенты ai, bi, ci, di найдем с условий в узлах интерполяции. ...
... видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы 1. Цель математической обработки результатов эксперимента; 2. Виды измерений; 3. Типы ошибок измерения; 4. Свойства случайных ошибок; 5. Почему среднеарифметическое значение случайной величины при нормальном законе ее ...
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
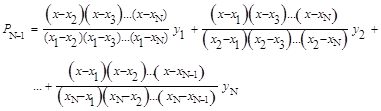
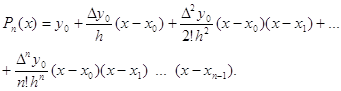

0 комментариев