Навигация
Проверить выполнение предпосылок МНК
3. Проверить выполнение предпосылок МНК
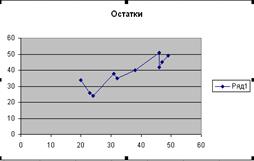
Проверим независимость остатков с помощью критерия Дарбина-Уотсона.
Вычислим коэффициент Дарбина-Уотсона по формуле:
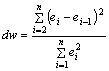 .
.
Данные для расчета возьмем из таблицы 2.
dw = 0,803
Сравним полученное значение коэффициента Дарбина-Уотсона с табличными значениями границ ![]() и
и ![]() для уровня значимости 0,05 при k=1 и n=10.
для уровня значимости 0,05 при k=1 и n=10. ![]() =0,88,
=0,88, ![]() =1,32, dw < d
=1,32, dw < d![]() , значит, остатки содержат автокорреляцию. Наличие автокорреляции нарушает одну из предпосылок нормальной линейной модели регрессии.
, значит, остатки содержат автокорреляцию. Наличие автокорреляции нарушает одну из предпосылок нормальной линейной модели регрессии.
Проверим наличие гетероскедастичности. Т.к. у нас малый объем выборки (n=10) используем метод Голдфельда-Квандта.
- упорядочим значения n наблюдений по мере возрастания переменной x и разделим на две группы с малыми и большими значениями фактора x соответственно.
- рассчитаем остаточную сумму квадратов для каждой группы.
Вычисления представим в таблицах 3 и 4.
Таблица 3. Промежуточные вычисления для 1-го уравнения регрессии.
| t | xi | yi | yi * xi | xi*xi |
|
|
|
| 1 | 27 | 46 | 1242 | 729 | 47 | -1 | 1 |
| 2 | 27 | 48 | 1296 | 729 | 47 | 1 | 1 |
| 3 | 28 | 47 | 1316 | 784 | 49,5 | -2,5 | 6,25 |
| 4 | 28 | 52 | 1456 | 784 | 49,5 | 2,5 | 6,25 |
| средн. знач. | 27,5 | 48,25 | |||||
|
| 1326,875 | ||||||
|
| 756,25 | ||||||
|
| 5310,00 | ||||||
|
| 3026,00 | ||||||
| n | 4 | ||||||
|
| 2,5 | ||||||
|
| - 20,5 | ||||||
|
| 14,5 |
Таблица 4. Промежуточные вычисления для 2-го уравнения регрессии.
| t | xi | yi | yi * xi | xi*xi |
|
|
|
| 1 | 37 | 63 | 2331 | 1369 | 63,789 | -0,789 | 0,623 |
| 2 | 38 | 69 | 2622 | 1444 | 64,582 | 4,418 | 19,519 |
| 3 | 39 | 62 | 2418 | 1521 | 65,375 | -3,375 | 11,391 |
| 4 | 41 | 67 | 2747 | 1681 | 66,961 | 0,039 | 0,002 |
| 5 | 44 | 67 | 2948 | 1936 | 69,340 | -2,340 | 5,476 |
| 6 | 46 | 73 | 3358 | 2116 | 70,926 | 2,074 | 4,301 |
| средн. знач. | 40,833 | 66,833 | |||||
|
| 2729,028 | ||||||
|
| 1667,361 | ||||||
|
| 16424 | ||||||
|
| 10067 | ||||||
| n | 6 | ||||||
|
| 0,793 | ||||||
|
| 34,448 | ||||||
|
| 41,310 |
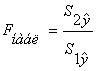 =
= ![]() =
=![]() 2,849
2,849
где ![]() - остаточная сумма квадратов 1-ой регрессии,
- остаточная сумма квадратов 1-ой регрессии, ![]() - остаточная сумма квадратов 2-ой регрессии.
- остаточная сумма квадратов 2-ой регрессии.
Полученное значение сравним с табличным значением F распределения для уровня значимости ![]() , со степенями свободы
, со степенями свободы ![]() и
и ![]() (
(![]() - число наблюдений в первой группе, m – число оцениваемых параметров в уравнении регрессии).
- число наблюдений в первой группе, m – число оцениваемых параметров в уравнении регрессии).
![]() ,
, ![]() , m=1.
, m=1.
Если 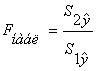 >
> ![]() , то имеет место гетероскедастичность.
, то имеет место гетероскедастичность.
![]() = 5,41
= 5,41
![]() <
< ![]() ,
,
значит, гетероскедастичность отсутствует и предпосылка о том, что дисперсия остаточных величин постоянна для всех наблюдений выполняется.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента ![]() .
.
Расчетные значения t-критерия можно вычислить по формулам:
![]() ,
, 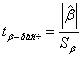
 ,
, 
![]() ,
,
![]()
![]()
![]()
![]() =35,5
=35,5
Промежуточные расчеты представим в таблице:
Таблица 5. Промежуточные вычисления для расчета t- критерия
| xi |
|
| 38 | 6,25 |
| 28 | 56,25 |
| 27 | 72,25 |
| 37 | 2,25 |
| 46 | 110,25 |
| 27 | 72,25 |
| 41 | 30,25 |
| 39 | 12,25 |
| 28 | 56,25 |
| 44 | 72,25 |
![]() =490,50
=490,50
![]()
![]()
![]()
![]()
![]() для уровня значимости 0,05 и числа степеней свободы n-2=8
для уровня значимости 0,05 и числа степеней свободы n-2=8
Так как ![]() и
и ![]() можно сделать вывод, что оба коэффициента регрессии значимые.
можно сделать вывод, что оба коэффициента регрессии значимые.
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера ![]() , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Коэффициент детерминации определяется по формуле:
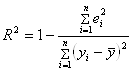
Из расчетов нам известно, что
![]() ;
; ![]() .
.
Рассчитаем ![]() :
:
Таблица 6. Промежуточные вычисления для расчета коэффициента детерминации.
|
|
|
|
| 69 | 9,6 | 92,16 |
| 52 | -7,4 | 54,76 |
| 46 | -13,4 | 179,56 |
| 63 | 3,6 | 12,96 |
| 73 | 13,6 | 184,96 |
| 48 | -11,4 | 129,96 |
| 67 | 7,6 | 57,76 |
| 62 | 2,6 | 6,76 |
| 47 | -12,4 | 153,76 |
| 67 | 7,6 | 57,76 |
![]()
![]() =930,4
=930,4
![]() =0,917.
=0,917.
Т.к. значение коэффициента детерминации близко к единице, качество модели считается высоким.
Теперь проверим значимость уравнения регрессии. Рассчитаем значение F-критерия Фишера ![]() по формуле:
по формуле:
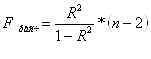
![]()
![]()
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. ![]() >
>![]() .
.
Средняя относительная ошибка аппроксимации находится по формуле:
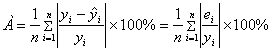
Таблица 7. Промежуточные вычисления для расчета средней относительной ошибки аппроксимации.
| yi |
|
|
| 69 | 6,305 | 0,091377 |
| 52 | 2,495 | 0,047981 |
| 46 | -2,186 | 0,047522 |
| 63 | 1,624 | 0,025778 |
| 73 | -0,247 | 0,003384 |
| 48 | -0,186 | 0,003875 |
| 67 | 0,348 | 0,005194 |
| 62 | -2,014 | 0,032484 |
| 47 | -2,505 | 0,053298 |
| 67 | -3,609 | 0,053866 |
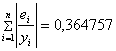
![]() ,
,
значит модель имеет хорошее качество.
Рассчитаем коэффициент эластичности по формуле:
![]()
![]()
6. осуществить прогнозирование среднего значения показателя Y при уровне значимости ![]() , если прогнозное значение фактора X составит 80% от его максимального значения.
, если прогнозное значение фактора X составит 80% от его максимального значения.
![]()
Рассчитаем стандартную ошибку прогноза
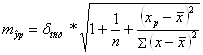 ,
,
где![]()
![]() =930,4 ;
=930,4 ; ![]()
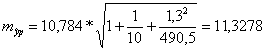
![]()
![]() ,
, ![]() для уровня значимости 0,1 и числа степеней свободы n-2=8
для уровня значимости 0,1 и числа степеней свободы n-2=8
![]()
Доверительный интервал прогноза:
![]()
![]()
Таким образом, ![]() =61,112 , будет находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048.
=61,112 , будет находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048.
Похожие работы
... города (Юго-запад, Красносельский район). 2) Составьте матрицу парных коэффициентов корреляции исходных переменных. Вместо переменной х2 используйте фиктивную переменную z. 3) Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов в линейной форме. Установите, какие факторы мультиколлинеарны. 4) Постройте модель у = f(х3, х6, х7, х8, z) в линейной форме. Какие факторы ...
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
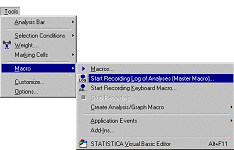
... широкие возможности по созданию макросов. В ходе написания данной курсовой работы был создан макрос на языке SVB для проверки гипотезы о нормальности остатков регрессии. Необходимость разработки данного приложения связана с особенностями осуществления регрессионного анализа в пакете STATISTICA. Написанный модуль был использован при эконометрическом моделировании вторичного рынка жилья в г. ...
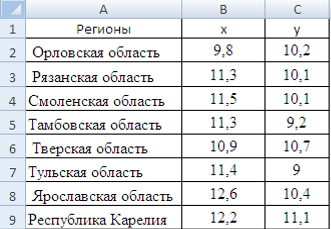
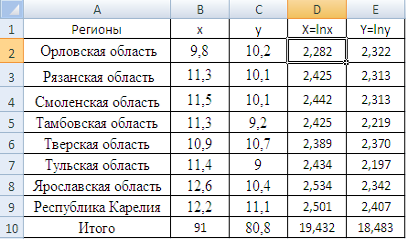
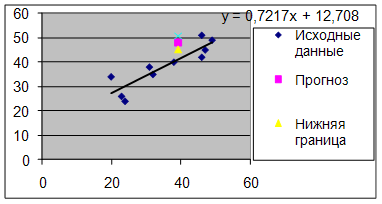
нты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. Решение 1. Уравнение линейной регрессии имеет вид: = а0 + а1x. Построим линейную модель. Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( ...

0 комментариев