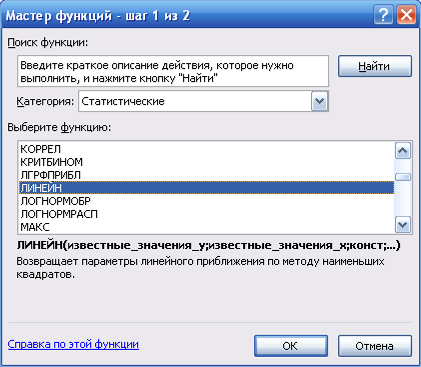
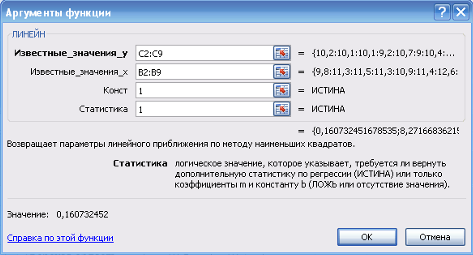
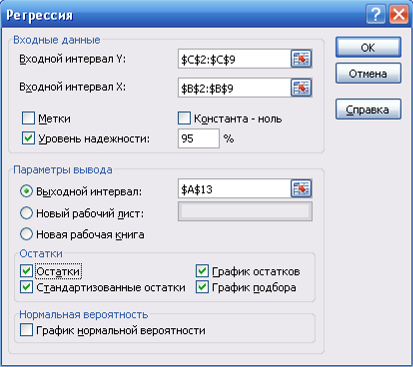
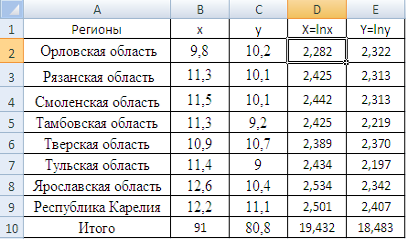
Навигация
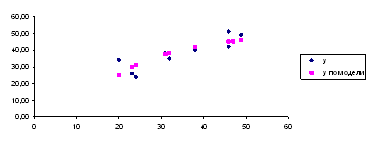
Представить графически фактические и модельные значения Y точки прогноза
7. Представить графически фактические и модельные значения Y точки прогноза.
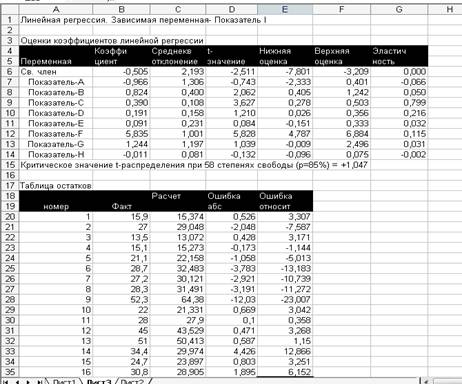
Воспользуемся данными из таблицы 2 для построения графиков с помощью MS Excel.
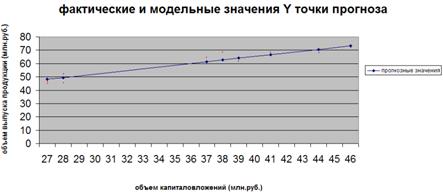
Рис. 2. Фактические и модельные значения Y точки прогноза.
8. Составить уравнения нелинейной регрессии: гиперболической, степенной, показательной. Привести графики построенных уравнений регрессии.
Построение степенной модели.
Уравнение степенной модели имеет вид:
![]()
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
![]()
Обозначим ![]() .
.
Тогда уравнение примет вид ![]() – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 1:
– линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 1:
Таблица 8. Расчет параметров уравнения степенной модели регрессии.
| t | xi | X |
| Y | YX | X*X |
|
|
|
|
| 1 | 38 | 1,5798 | 69 | 1,839 | 2,905 | 2,496 | 62,347 | 6,653 | 9,642 | 44,26 |
| 2 | 28 | 1,447 | 52 | 1,716 | 2,483 | 2,094 | 50,478 | 1,522 | 2,926 | 2,315 |
| 3 | 27 | 1,431 | 46 | 1,663 | 2,379 | 2,048 | 49,225 | -3,225 | 7,010 | 10,399 |
| 4 | 37 | 1,568 | 63 | 1,799 | 2,821 | 2,459 | 61,208 | 1,792 | 2,845 | 3,212 |
| 5 | 46 | 1,663 | 73 | 1,863 | 3,098 | 2,765 | 71,153 | 1,847 | 2,530 | 3,411 |
| 6 | 27 | 1,431 | 48 | 1,681 | 2,406 | 2,049 | 49,225 | -1,225 | 2,552 | 1,5 |
| 7 | 41 | 1,613 | 67 | 1,826 | 2,945 | 2,601 | 65,771 | 1,289 | 1,924 | 1,66 |
| 8 | 39 | 1,591 | 62 | 1,793 | 2,853 | 2,531 | 63,477 | -1,477 | 2,382 | 2,182 |
| 9 | 28 | 1,447 | 47 | 1,672 | 2,419 | 2,094 | 50,478 | -3,478 | 7,4 | 12,099 |
| 10 | 44 | 1,644 | 67 | 1,826 | 3,001 | 2,701 | 68,999 | -1,999 | 2,984 | 3,997 |

![]()
![]()
Уравнение регрессии будет иметь вид:
![]()
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
![]()
![]()
Вычислим коэффициент детерминации ![]() :
:
![]() =930,4;
=930,4; ![]()
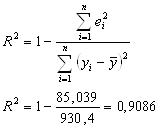 (1)
(1)
Вычислим среднюю ошибку аппроксимации А:
![]() %
%
 (2)
(2)
Коэффициент эластичности рассчитывается по формуле:
![]() (3)
(3)
![]()
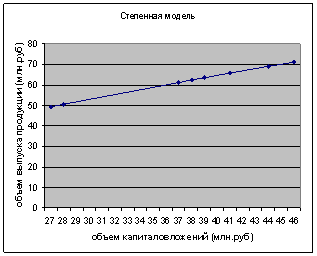
Рис. 3. График степенного уравнения регрессии.
Построение показательной функции.
Уравнение показательной кривой:![]()
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
![]()
Обозначим ![]()
Получим линейное уравнение регрессии:
![]()
Рассчитаем его параметры, используя данные таблиц 1 и 8.
Промежуточные расчеты представим в таблице 9.
Таблица 9. Промежуточные расчеты для показательной функции.
| t | xi | Y |
| y |
|
|
|
|
| 1 | 38 | 1,839 | 69,882 | 69 | 62,632 | 6,368 | 10,167 | 40,552 |
| 2 | 28 | 1,716 | 48,048 | 52 | 49,893 | 2,107 | 4,223 | 4,44 |
| 3 | 27 | 1,663 | 44,901 | 46 | 48,771 | -2,771 | 5,682 | 7,68 |
| 4 | 37 | 1,799 | 66,563 | 63 | 61,224 | 1,776 | 2,901 | 3,155 |
| 5 | 46 | 1,863 | 85,698 | 73 | 75,128 | -2,128 | 2,832 | 4,528 |
| 6 | 27 | 1,681 | 45,387 | 48 | 48,771 | -0,771 | 1,581 | 0,595 |
| 7 | 41 | 1,826 | 74,866 | 67 | 67,054 | -0,054 | 0,08 | 0,003 |
| 8 | 39 | 1,793 | 69,927 | 62 | 64,072 | -2,072 | 3,235 | 4,295 |
| 9 | 28 | 1,672 | 46,816 | 47 | 49,893 | -2,893 | 5,798 | 8,369 |
| 10 | 44 | 1,826 | 80,344 | 67 | 71,788 | -4,788 | 6,669 | 22,921 |
![]() =63,2432
=63,2432
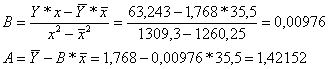
Уравнение будет иметь вид:
![]()
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
![]()
Рассчитаем коэффициент детерминации по формуле (1).
![]() =930,4;
=930,4; ![]()
![]()
Вычислим среднюю ошибку аппроксимации А по формуле (2):
![]()
А=0,1*43,170=4,317%
Коэффициент эластичности рассчитаем по формуле (3):
![]() %
%
Построим график функции с помощью MS Excel.
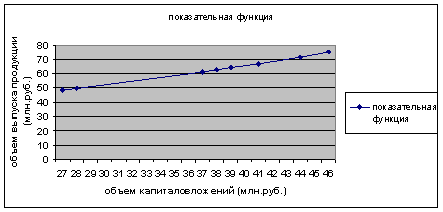
Рис. 4. График показательного уравнения регрессии.
Построение гиперболической функции.
Уравнение гиперболической функции ![]()
Произведем линеаризацию модели путем замены Х=1/х.
В результате получим линейное уравнение: ![]()
Рассчитаем параметры уравнения, промежуточные вычисления представим в таблице 10.
Таблица 10. Расчет параметров для гиперболической модели.
| t | xi | yi | X=1/xi | y*X |
|
|
|
|
|
| 1 | 38 | 69 | 0,02632 | 1,81579 | 0,00069 | 63,5648 | 5,4352 | 7,877 | 29,5409 |
| 2 | 28 | 52 | 0,03571 | 1,85714 | 0,00128 | 50,578 | 1,422 | 2,7346 | 2,0221 |
| 3 | 27 | 46 | 0,03704 | 1,7037 | 0,00137 | 48,7502 | -2,7502 | 5,9787 | 7,5637 |
| 4 | 37 | 63 | 0,02703 | 1,7027 | 0,00073 | 62,5821 | 0,4179 | 0,6634 | 0,1747 |
| 5 | 46 | 73 | 0,02174 | 1,58696 | 0,00047 | 69,8889 | 3,1111 | 4,2618 | 9,6791 |
| 6 | 27 | 48 | 0,03704 | 1,77778 | 0,00137 | 48,7502 | -0,7502 | 1,563 | 0,5628 |
| 7 | 41 | 67 | 0,02439 | 1,63415 | 0,00059 | 66,2256 | 0,7744 | 1,1559 | 0,5998 |
| 8 | 39 | 62 | 0,02564 | 1,58974 | 0,00066 | 64,4972 | -2,4972 | 4,0278 | 6,2362 |
| 9 | 28 | 47 | 0,03571 | 1,67857 | 0,00128 | 50,578 | -3,578 | 7,6128 | 12,8021 |
| 10 | 44 | 67 | 0,02273 | 1,52273 | 0,00052 | 68,5235 | -1,5235 | 2,2738 | 2,3209 |

![]()
![]()
![]()
![]()
Уравнение гиперболической модели:
![]()
Рассчитаем коэффициент детерминации по формуле (1).
![]() =930,4;
=930,4; ![]()
![]()
Вычислим среднюю ошибку аппроксимации А по формуле (2):
![]()
А=0,1*38,1488=3,81488%
Коэффициент эластичности рассчитаем по формуле (3):
![]()
![]() %
%
Построим график функции с помощью MS Excel.
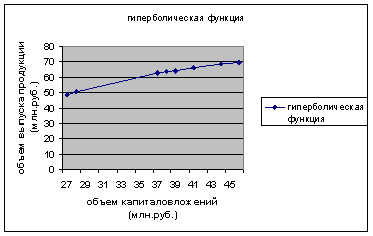
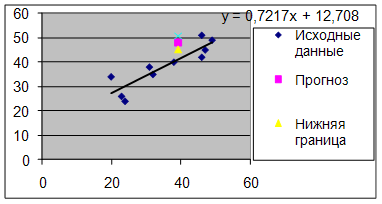
Рис. 5 График гиперболического уравнения регрессии.
9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать выводы.
Коэффициенты были рассчитаны в задании 8. Для сравнения моделей составим сводную таблицу 11:
Таблица11. Сводная таблица характеристик моделей.
| параметры модель | Коэффициент детерминации, R | Коэффициент эластичности, | Средняя относительная ошибка аппроксимации, А (%) |
| Линейная | 0,917 | 0,788 | 3,648 |
| Степенная | 0,909 | 0,692 | 4,22 |
| Показательная | 0,896 | 0,817 | 4,317 |
| Гиперболическая | 0,923 | 0,638 | 3,815 |
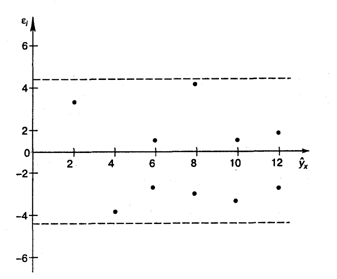
Для всех моделей средняя относительная ошибка аппроксимации не превышает 7%, значит, качество всех моделей хорошее. Коэффициент детерминации более приближен к 1 у гиперболической модели, таким образом, эту модель можно взять в качестве лучшей для построения прогноза. Для гиперболической модели степень связи между факторным и результативным признаком самая низкая, т.к. ![]() имеет наименьшее значение, а для показательной модели самая высокая, т.к. коэффициент эластичности наибольший.
имеет наименьшее значение, а для показательной модели самая высокая, т.к. коэффициент эластичности наибольший.
Похожие работы
... города (Юго-запад, Красносельский район). 2) Составьте матрицу парных коэффициентов корреляции исходных переменных. Вместо переменной х2 используйте фиктивную переменную z. 3) Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов в линейной форме. Установите, какие факторы мультиколлинеарны. 4) Постройте модель у = f(х3, х6, х7, х8, z) в линейной форме. Какие факторы ...
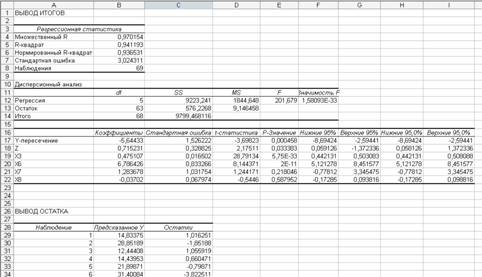
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... широкие возможности по созданию макросов. В ходе написания данной курсовой работы был создан макрос на языке SVB для проверки гипотезы о нормальности остатков регрессии. Необходимость разработки данного приложения связана с особенностями осуществления регрессионного анализа в пакете STATISTICA. Написанный модуль был использован при эконометрическом моделировании вторичного рынка жилья в г. ...
нты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. Решение 1. Уравнение линейной регрессии имеет вид: = а0 + а1x. Построим линейную модель. Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( ...

0 комментариев